CFRP 重型机床传动系的挠曲振动研究

2020-11-23文湘隆李文虎

机械设计与制造 2020年11期

文湘隆，方圆，杨沫，李文虎

（武汉理工大学机电工程学院，湖北武汉 430070）

1 引言

重型机床传动轴由于跨距长、质量大、转速高，即使是很小的偏心距也会产生非常大的不平衡离心力，使轴系产生振动噪声，严重降低机床加工精度。金属材料自身的局限性限制了传动轴动态性能的提升，采用CFRP 制备的传动轴是解决重型机床传动轴系振动问题的重要途径之一[1]。

目前关于复合材料传动轴的研究主要集中在铺层设计参数对轴管的扭转强度、屈曲扭矩、固有频率和扭转刚度的影响规律和实验研究[2-4]。文献[5]采用理论计算和有限元分析计算了CFRP传动轴临界转速，证明了两种方法的可行性并找出了两者结果差异的原因。文献[6]提出了复合材料传动轴简支条件下的动力学模型，对系统动力学方程进行近似求解，得到了复合材料轴系的一阶模态和振型。文献[7]采用Euler-Bernoulli 梁理论建立复合材料汽车传动轴系的动力学方程，该动力学模型考虑了两段式正交铺层的复合材料传动轴管以及传动轴中间万向节，分析得到两段式复合材料汽车传动轴的简支模态。文献[8-9]对复合材料轴的转子动力学进行了相关研究，得到了复合材料轴的固有频率主要受到铺层角度和比例的影响。

所有这些相关的研究为复合材料传动轴的固有频率设计提供了相关理论方法，结合复合材料层合理论和轴系弯振的传递矩阵法，系统性的研究CFRP 传动轴系的弯曲振动，并采用ABAQUS 对轴系进行了模态仿真，与理论预测模型进行了对比。

2 CFRP 轴系动力学模型

重型机床传动轴系简图，如图1 所示。轴系由滚动轴承、金属轴段、刚性联轴器、CFRP 轴管组成，左端连接的是变速器的输出端，右端连接刀具主轴箱的输入端。传动轴系统的各段尺寸参数，如表1 所示。CFRP 传动轴全长2300mm。整个轴系由滚动轴承支撑，支承刚度为1×109N/m。轴系全长为3115mm，最大扭转力矩3000Nm。

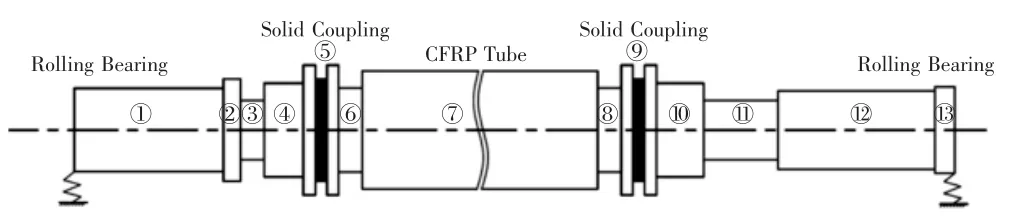
图1 重型机床CFRP 传动轴系Fig.1 CFRP Driveline System of Heavy Duty Machine Tool

表1 CFRP 传动系的截面参数Tab.1 Section Parameters of CFRP Driveline

2.1 CFRP 轴管设计

传动轴管壁厚t=7.2mm，采用单向T700/YPH-308 碳纤维预浸料（性能参数如表2 所示）缠绕成型，单层厚度为0.2mm。文献[10]已详细阐述CFRP 传动轴关于满足强度刚度的设计和校核方法，本文不再赘述。通过各种方案扭转强度比较，最终确定铺层方案为［±45/（±15）3/±45/（±15）3/±45］S，这将为CFRP 轴系弯曲振动提供计算依据。

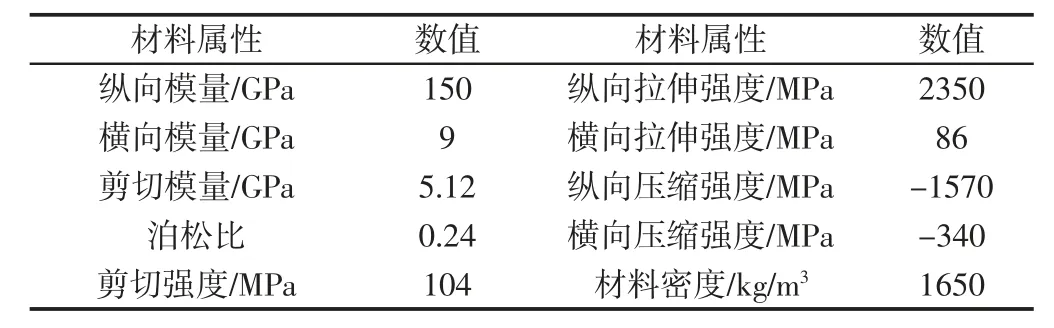
表2 T700/YPH-308 的材料属性Tab.2 Material Properties of T700/YPH-308

2.2 CFRP 轴系传递矩阵

传递矩阵法是将质量连续分布的弹性转子离散为不同的盘轴单元。将图1 中的CFRP 传动系统简化为n 个无厚度刚性薄圆盘和n-1 个无质量弹性轴段的盘轴单元组成的链状系统，如图2所示。对于弯曲刚度各向同性的转子系统，仅分析垂直方向弯曲变形即可。设 mi，li，yi和 θi分别表示第 i 个圆盘单元的质量、长度、垂直方向位移和yoz 垂面内角位移，Mi和Qi分别为第i 个单元截面上的弯矩和剪力，Jp和Jd为圆盘极转动惯量和直径转动惯量。因此圆盘单元 i 的惯性力为 mω2yi，惯性力矩为（Jp-Jd）ω2θi。

图2 刚性薄圆盘和弹性轴模型Fig.2 Rigid Thin Disk and Elastic Shaft Model

基于达朗伯原理，结合盘轴单元的受力，圆盘单元状态变量从i 到i+1 的传递关系可表示为：

式中：［Ts］i—刚性薄圆盘的状态传递矩阵

对于CFRP 轴段和金属轴段，刚性薄圆盘的状态传递矩阵均可使用式（3）。而对于弹性轴的传递矩阵，复合材料轴段和金属轴段具有明显差异，金属轴段的弹性轴的状态传递关系可表示如下：

基于复合材料层合理论和Layer-wise 理论，得到复合材料轴管的等效弯曲刚度为（5），式中分别表示第k 层复合材料外表面、内表面处的半径。

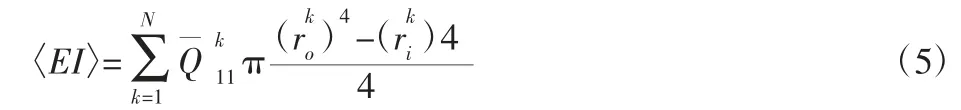
综合刚性薄圆盘、金属弹性轴段和CFRP 弹性轴段的传递关系，图3 中的CFRP 轴系盘轴模型两端状态变量的传递关系可表示为：

由于轴系两端由滚动轴承支撑，具有一定的支撑刚度，因此轴系两个端面的垂直方向位移和yoz 垂面内角位移的自由度没有完全限制，而弯矩和剪力可以确定恒为0。因此轴系的边界条件为：

扩展式（6）和利用式（8）的边界条件可得：

方程组（9）存在非零解的条件需满足下列条件：

满足式（10）的ω 值即为轴系的临界角速度。在求解轴系的弯曲振动频率时，可以将ω 作为横坐标，剩余量Δ（ω）为纵坐标，利用MATLAB 软件进行试算，画出角速度和剩余量的曲线，该曲线与Δ（ω）=0 的交点即为轴系的临界角速度，然后利用公式f=ω/2π 即可求得轴系的弯曲振动频率。

3 结果与讨论

在这部分，轴系弯曲振动传递矩阵法、模态仿真和简支梁模型三种方法计算的结果得到对比。有限元计算结果可用于验证传递矩阵法计算CFRP 轴系振动的准确性。

3.1 CFRP 传动轴系传递矩阵计算结果

根据表1 的CFRP 传动轴系的尺寸参数，结合CFRP 轴管的铺层参数，划分各轴段编号N，盘轴单元数目n 和各盘轴单元的参数，如表3 所示。

表3 重型机床CFRP 轴系的相关数据Tab.3 Relevant Data of CFRP Shafting for Heavy Machine Tools

结合式（2）～式（5）和式（7）得到 CFRP 轴系的盘轴模型的整体传递矩阵，由边界条件式（10）得到系统的剩余量Δ（ω），应用MATLAB 软件绘制角速度和剩余量的关系曲线，如图3 所示。剩余量Δ（ω）＝0 与曲线的第一个交点对应的角速度为264rad/s，因此CFRP 轴系的第一阶弯曲振动频率为42.02Hz，对应的转速为2521r/min。

图3 角速度与剩余量关系曲线图Fig.3 Relation Graph of Angular Velocity vs. Δω

3.2 CFRP 传动轴系有限元计算结果

在有限元软件ABAQUS 中按照图1 的尺寸建立轴系模型并装配，赋予材料属性并定义铺层，划分结构化网格。设置滚动轴承的支撑刚度，进入interaction 模块，选择Special-Springs/Dashpots，创建接地弹簧，刚度设置为1×109N/m，限制在一个自由度方向上。对CFRP 传动轴系进行自由模态仿真分析。一阶振型，如图4 所示。CFRP 传动轴系的一阶固有频率ω=42.05Hz，对应转速为2523.18r/min。

图4 CFRP 传动系一阶弯曲振型Fig.4 First Order Bending Mode of CFRP Drive-Line

3.3 简支梁模型计算结果

不考虑CFRP 传动轴的金属连接件，将复合材料传动轴简化为均质简支梁，其计算公式为：

带入CFRP 传动轴的参数，式中m 为单位长度质量，L 取整个传动轴系长度，计算得到一阶弯曲固有频率为：f=51.2Hz，对应转速为3072r/min。

综合对比CFRP 传动轴系的传递矩阵法、简支梁模型和有限元仿真结果可以发现简支梁模型在预测CFRP 传动轴系时存在明显的误差，如表4 所示；而推导的传递矩阵法可以准确的预测CFRP 传动轴系的一阶弯曲振动转速，误差仅为0.086%。这是由于简化均质简支梁模型在计算轴系振动时没有考虑金属部件对轴系动态性能的影响。而传递矩阵法在计算轴系弯曲振动时，既考虑了CFRP 轴管的各向异性，又考虑了轴系金属部件的影响，因此能够较为准确的预测复合材料传动轴系的振动性能。