浙江成品油管网调度计划编制软件的开发与应用

阮亦根 梁永图 郑荣荣

〔1.中国石化浙江石油分公司 浙江杭州 310000；2.中国石油大学（北京）城市油气输配集输北京市重点实验室 北京 102249〕

中国石化浙江石油分公司成品油管道调控中心运行调度甬绍金衢、浙赣东线、甬台温、绍兴-杭州、诸暨-桐庐管道，总里程达1490km，有2座首站、1座中间注入站、1座加压泵站、5座分输泵站、8座分输站，呈现管径大、分输量前多后少、泵站多、变径多等特点，管输工艺复杂、油品与沿线需求变化频繁、需中间站注入等情况，导致人工编制管输计划工作繁重、时效性差。为了能够满足现场生产需求，与中国石油大学（北京）合作研发了浙江成品油管网调度计划编制软件。

1 技术要点

成品油管道运行时需要输送多种油品，首站注入与下载站下载不同步，因各站需求不同工况变化较大，这些因素导致求解困难。国内已有编制软件但因需大量人工设定，约束条件时常不能满足等原因，导致不能满足现场需要[1-3]。

调控中心负责调度的管道具有许多工艺特点：由变径多导致不同混油界面流量上下限不同；因各分输站油品的罐容不同导致下载不同油品流量上下限不同；由于部分下载站没有混油罐，导致混油操作要求不同；因地形原因导致不同站场压力控制要求多样，为此，只有跟踪批次界面才能适应上述工艺特性。

2 理论依据

国内外学者深入研究了多条管道调度运行工作，D.C.Cafaro[4，5]和S.Relvas[6]研究了单注入点管道运行，S.A.MirHassani[7]和P.M.Castro[8]研究了枝状管道运行，D.C.Cafaro[9-11]等后续研究了管网运行，ZhangHR[12-14]等的理论模型，采用蚁群算法（ACO）和单纯形法（SM）混合求解。

3 调度计划数学模型

3.1 模型假设

假设条件：管道末站只需考虑流量限制条件；不需计算混油长度，将混油段简化为混油界面；油品是不可压缩的；同一时间窗内各站下载流量不变；各站库容满足下载计划量。

3.2 目标函数

软件以结果与计划体积偏差最小为目标函数[15-22]，将计划起终时间、各站下载起终时间、批次切换时间等为时间节点[23]，用连续时间表达法[24，25]，综合考虑了时间节点、流量、计划量等约束条件[26，27]。

式中：Vxi，j、Vsi，j是第i站对第j批次的计划量、下载量，m3；i为下载站场编号；j为油品批次编号；I是下载站编号集合；Ji是第i站有分输需求，且初始时刻批次油尾未过该站各批次编号集合。

3.3 约束条件

3.3.1 时间节点约束

假设各个时间节点按照先后顺序排列，前一批次油头到站时间节点不晚于后一批次油头到站时间节点。

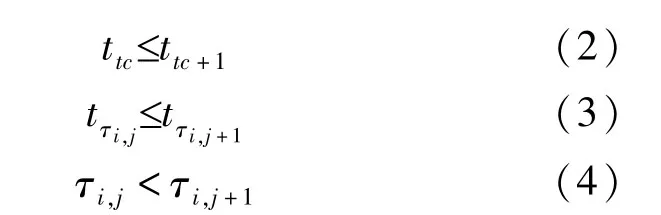
同一批次油头到达前一站场时刻要早于到后一站场时刻。

站场对有需求批次开始下载时间一定不小于该批次到站时间，结束下载时间不大于下一批次油头到站时间。

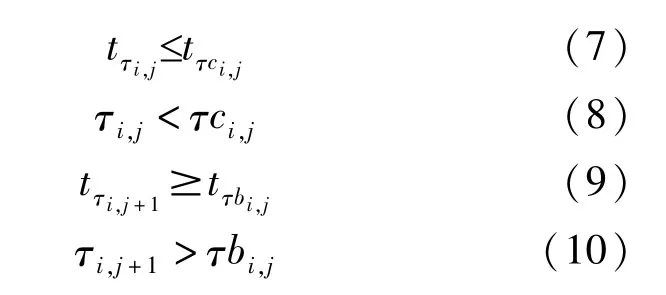
站场对该批次开始下载时间不晚于该批次结束下载时间。

站场对批次开始下载时间不早于计划开始时间，下载结束时间不晚于计划结束时间。

式中：ttc是第tc时间节点对应的时间；τi，j是第j批次油头到达第i站时间节点编号；τci，j、τbi，j是第i站对第j批次开始下载、结束下载时间节点编号；ttc和ttb为计划开始和结束时间；τtc和τtb为计划开始和结束时间节点编号。

3.3.2 批次运移约束

任意时间窗内第i站与第i+1站间管线允许的最小流量与时间窗长度乘积，不能大于该时间窗内首站注入体积与该时间窗内第i站及第i站之前各站分输体积之差。任意时间窗内第i站与第i+1站间管线允许的最大流量与时间窗长度乘积，不能小于该时间窗内首站注入体积与该时间窗内第i站及第i站之前各站分输体积之差。

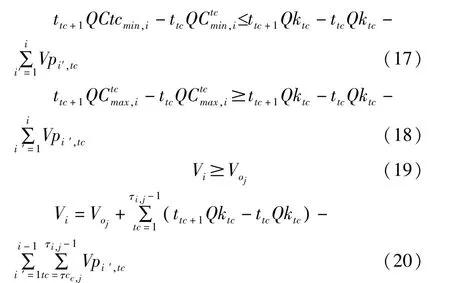
式中QCtcmin，i是第tc时间节点与第tc+1时间节点之间第i站和第i+1站间管段允许最小流量，m3/h；QCtcmax，i是第tc时间节点与第tc+1时间节点之间第i站和第i+1站间管段允许最大流量，m3/h；Qktc是第tc时间节点与第tc+1时间节点之间首站注入量，m3；i＇为下载站站场编号；Vi是第i站体积坐标；Voj是第j批次油头的初始体积坐标。

3.3.3 下载计划约束

某站对某批次实际下载体积为该批次油头到该站时间节点与下一批次油头到该站的时间节点之间所有时间窗内下载体积的总和。

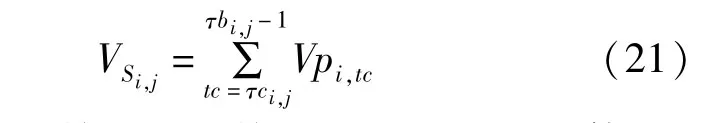
式中VSi，j是第i站对第j批次实际下载体积，m3；Vpi，tc是第i站在tc和tc+1时间节点间时间窗内下载的体积中间变量，m3。

3.3.4 模型求解程序

以原管道内油品界面为初始条件，用蚁群算法求解，算法程序见图1。

图1 算法程序框图

4 启泵理论模型

在满足压力约束条件下，由能量平衡方程优化并确定启泵方案，而使目标函数总运行成本最小，从而实现对成品油管网运行方案的优化。

对设有N个泵站且第i泵站配置k台离心泵的成品油管网系统，当泵转速固定且不考虑电价波动时，以使总运行成本（目标函数）最小为优化管输计划。目标函数为：

式中：Y是总运行成本，元；T是输送周期，s；F是用电费用，元；ηij、Cij是经过第i泵站第j台泵的泵效、运行状态；aij是第i泵站第j台泵流量Q=0提供的扬程，bij是第i泵站第j台泵流量Q=Qij时需要的扬程。

4.1 压力约束

式中：pini是第i个泵站的油品进站压力，Pa；pin-mini是第i个泵站最低进站压力，Pa；pin-maxi是第i个泵站最高进站压力，Pa；px是管道任意点处的剩余压力，Pa；pmax是管道最大可承载压力，Pa；pmin是所输送油品的饱和蒸汽压，Pa；pouti是第i个泵站油品出站压力是第i个泵站油品最大出站压力，Pa。

4.2 流量约束

式中：Qij是过泵实际流量，m3/h；Qmaxj是泵设计最大流量，m3/h；Qmin、Qmax是管道最小、最大流量，m3/h；Vi、Vplani是分输站的结果、计划分输量，m3；

4.3 泵站特性约束

对于转速不变的泵机组，可通过实际运行数据，采用最小二乘法确定泵的特性方程。

若泵站由多泵串联组合，可计算出泵组合数和泵机组提供的扬程。任一泵站，若存在X种泵组合方式，则：

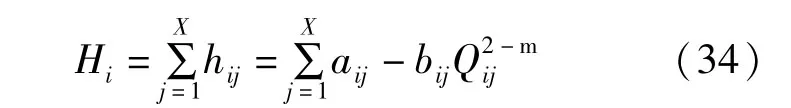
式中：Hi为第i泵站提供的扬程，h；hij为第i泵站第j台泵提供的扬程，h；；Aij，Bij，Cij为泵的效率曲线的特性系数。

同时，各个泵站要满足开泵方案数目的约束条件：

式中n是泵站开泵方案数目；M是不同型号泵可排列组合的泵机组数目。

5 模型求解

求解分为两部分，第一部分求出最优目标函数的函数值，第二部分通过递推的方法确定每个泵站的状态变量和决策变量，从而确定全线启泵方案。

6 计划编制软件及应用

软件由计划管理、静态数据、动态数据、批次计划、启泵方案和帮助6大模块组成，在交互界面填入相关参数，便可开始编制计划，软件可自动生成批次图、计划表、时刻表及调度令。软件数据结构示意见图2和图3。

图2 软件数据结构示意图

图3 软件数据结构示意图

在输油过程中，若需改变原计划量，可在软件中设置当前工况为初始条件，按新计划编制新计划，方便快捷。

以甬绍金衢管道某年8月20日输油为例，生成的计划、启泵方案分别见表1、表2。

表1 编制结果对比表

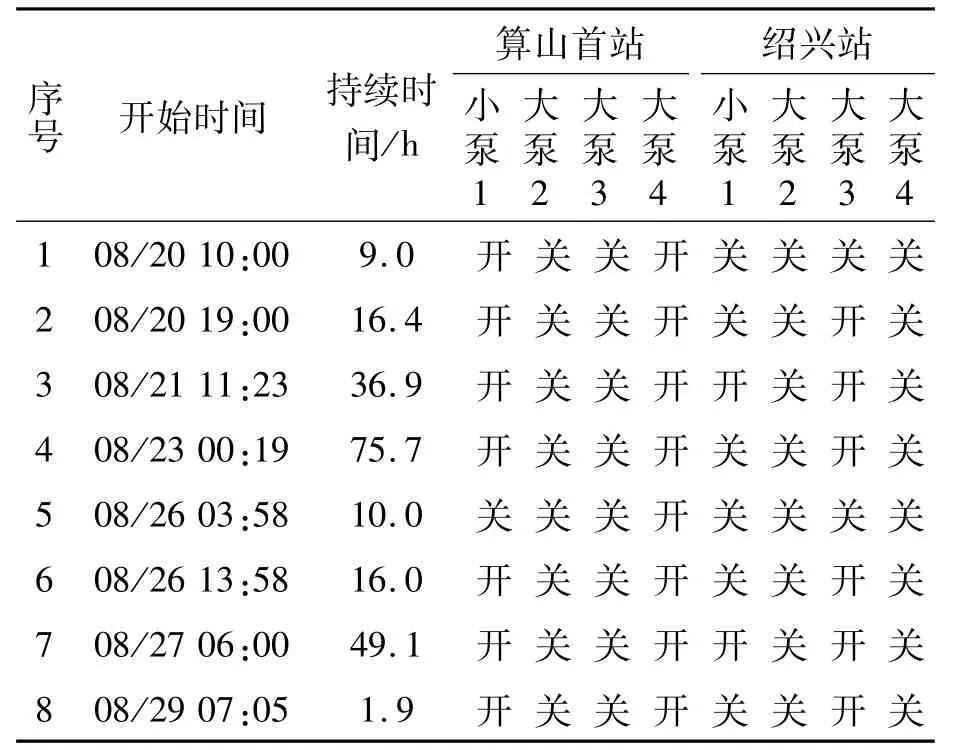
表2 软件计算得出的启泵方案

从表1、表2可看出，运行方案首站注入量变化小、泵避免了短时启停，各站结果与计划量基本一致，可操作性强。

7 结语

通过以甬绍金衢管道在某年8月20日输油为例和4年来的应用表明，浙江成品油管网调度计划编制软件具有运行可靠、编制方案可行的特点，还可根据现场需要生成调度令等报表，实现了自动编制报表，方便快捷，在现场应用中取得了很好的成效。