平衡吊杆系平衡条件分析

朱晓慧 任延举 童天业

摘要：本文分析介绍了平衡吊的工作原理，并根据实际使用情况，建立其杆系的三维模型，在对其平衡条件进行分析时，将模型进行简化，进而分析其平衡时的运动及受力情况，给出相关计算分析。

关键词：平衡吊;平衡条件;杆系分析

1平衡吊的结构和工作原理

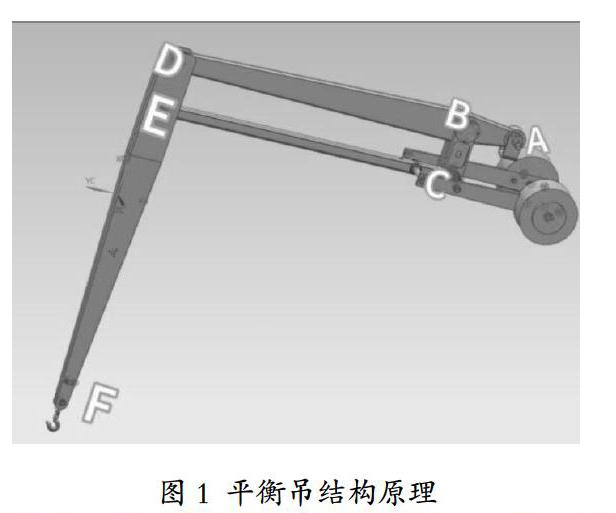
平衡吊的结构如图1所示，主要分为传动、杆系和回转机构三个部分。

传动部分是完成起吊重物功能的机构，由电动机、减速器、联轴器等带动丝杠回转，驱使螺母升降，从而完成吊钩在垂直方向的升降运动。该部分也可由气缸、油缸代替完成起重物的功能。

杆系部分是一平行四连杆机构，它由ABD、DEF、BC、CE 四杆组成，在B、C、D、E处用铰链连接，其中 BC与DE并行且相等，BD 与CE平行且相等。在C点安装有滚轮，可以沿水平导轨滚动，当 C点沿水平方向移动时，吊钩F点作水平运动。传动部分和杆系通过回转机构安装在立柱上，可以使吊钩绕立柱回转360°。

平衡吊的水平运动和绕立柱的回转运动，用手在吊钩处轻轻推动即可获得，而升降运动可以通过操作按钮由电机来完成。

2平衡吊的平衡条件

平衡吊的平衡是指：吊钩F点无论空载还是负载，运行到工作范围内的任何位置后都可以随意停下并保持静止不动，即达到随遇平衡状态。

由图l可知A点的运动是由传动部分控制的，当在一定高度时，可以将A点看作一个固定铰链支座，C点的水平移动是引起F点水平运动的原因，如果吊钩F在任何位置（起重或空载）时，F点、C点、A点只有垂直方向的反力且合力为零，那么支座C点的水平受力为零，平衡就可以得到。

为便于分析问题，假设杆系的自重及各铰链点之间的摩擦均忽略不计。根据静力学的原理，平面力系中某一杆件同时受三力作用，则三力必交于一点，叫做三力杆。某一杆件同时受二力作用且二力的作用点在两个端点，则二力必然大小相等方向相反，叫二力杆。故CB、CE为二力杆。其受力方向沿铰链连线。ABD、DEF为三力杆。三力平衡时，其力必汇交于一点。

先分析DEF杆件。在F点吊起重物时，其方向垂直向下，CE杆通过铰链E压给DEF杆的作用力的方向为沿CE连线方向，力与交于K点，则第三个力，即ABD杆通过铰链D作用于DEF杆的力，必通过D点交于K点方向可由力三角形得出。

其次再分析ABD杆件，根据作用与反作用的道理，显然，杆件DEF通过铰链D给杆ABD以反作用′。二力杆BC通过铰链B给杆ABD的作用力沿BC方向，′力与力交于J点，则第三个力即固定铰链A对ABD杆的支反力必然通过J点，其方向由力三角形提出。

如前所述，平衡吊要达到平衡，支反力必须为铅垂方向的力。现在将这两个构件的受力分析综合到一起来研究。

由于在力多边形中，力与力同为铅垂方向，力与力的水平投影是等长的，即力与的水平分力大小相等方向相反，处于平衡状态，故C点无水平分力。

在此种条件下才能保证支反力保持铅垂方向，根据上述受力分析，只有当机构在任意一个位置下，都能做到：过F点做一条铅垂线FK与EC杆的延长线相交于K 点，再连接K、D两点并延长与BC杆的延长线相交于J点，而J点正好过A点所作的铅垂线上，才能使支反力保持铅垂方向。

要做到这一点，满足机构的几何条件为：

△KEF ∽ △ABJ;△KDE ∽ △DJB

相似三角形的对应边成比例关系，得到：

EF∶EK = BJ∶AB;DE∶EK = BJ∶BD

由以上两式得到：EF∶DE = BD∶AB

假設：ABD = H，AB = h，BD = H1，DEF = L， DE = l， EF = L1

则：

即： ，其中为放大系数。

这就是说，只要杆系各杆件满足上述关系式，机构即可在任意位置达到平衡。

同时，从图2中还可以看到另一个重要现象，即A，C，F三点共线。证明如下：

∵FE∥BC   ∴

∵EC∥AB   ∴

又∵∠FEC  = ∠CBA

∴ △FEC ∽ △CBA

得到 ：FC∥CA

因为C点为FC和CA的共同点，所以FC与CA必须在同一直线上，即F，C，A三点共线。

3总结

上述平衡吊杆系结构的平衡条件分析鉴于理论分析及工程应用为基础，针对具体不同型号、结构形式、使用场合的平衡吊，应根据具体情况进行分析计算，可详细地对杆系中各危险截面进行单元化分析。

作者简介：朱晓慧，出生年月：1983年10月，广西大学硕士研究生，现就职于沈阳工学院。