会“跳动”的表格

黄旭军

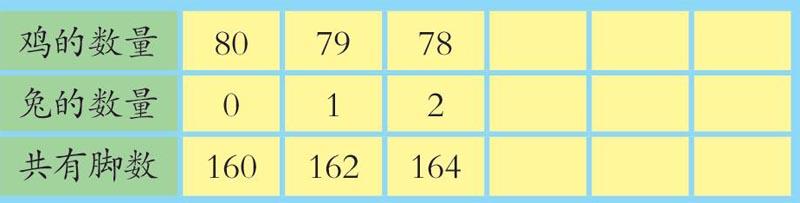
阿木老师风风火火地走进了教室，飞快地在黑板上画了个空表格。这时上课铃正好响起，阿木老师严肃地对大家说：“今天我们要学习列表法！”

同学们一脸茫然。然后阿木老师在黑板上写了一道鸡免同笼的题目：把鸡和兔放在同一个笼子里，鸡和兔共有80只，共有脚200只，鸡和兔各有多少只？

数学课代表忍不住了，站起来说：“老师，列表法我们早学会了呀。”

班长也接着说：“老师，您是上复习课吗？可是这么大的数据，用列表法岂不是要列上百格？”

班上的“数学王子”也说：“列表法的缺点就是数据太多时做起来不方便，这不是您说的吗？”

阿木老师对着几位同学哈哈一笑，神秘地说：“因为今天我们要学的是不一样的列表法！”

同学们将信将疑：“解‘鸡兔同笼用假设法不是很方便吗？为什么又要教列表法？”

阿木老师二话不说，自己直接在表上填了起来。

同学们在下面看笑话，这样下去，可以把四米长的黑板从最左边列到最右边！

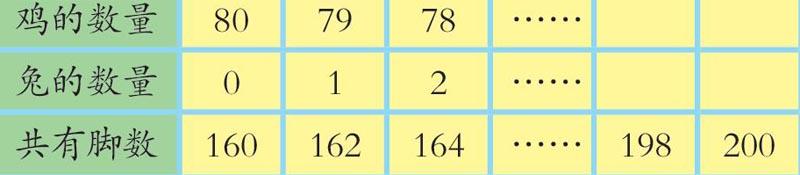
阿木老师突然停下，然后说：“这要列到什么时候呀，我要跳过一部分！”接着又写了几个数据。

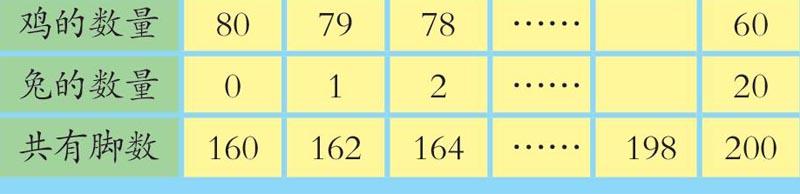
数学课代表一拍桌子，叫道：“我知道了，找规律直接填数就行了！”阿木老师示意他接着说。数学课代表指着表格说：“每次变化两只脚，从160到200共相差了40只脚，变化了20次，也就是兔子从0变成了20，所以兔有20只，鸡有60只！”

阿木老师笑了：“一个简单的列表法，用跳跃思维来做，是不是也很方便？这就是我发明的跳跃列表法，用它不但可以解决鸡兔同笼问题，还可以解决其他难题呢！”

例1

鸡和兔放在同一个笼子里，鸡比兔多26只，共有脚274只，鸡、兔各有几只？

可以把鸡分成两部分，一部分是与兔的数量相同，另一部分是比兔的数量多。

已知鸡比兔多26只，多出来的这些鸡的脚有2×26=52（只），又知鸡、兔共有脚274只，它包括两个部分，一部分是比兔多的26只鸡的脚的数量，即52只。另一部分是同样多的鸡和兔的脚的总数，即274-52=222（只）。又因为一只鸡和一只兔的足数和是2+4=6（只），所以兔的数量是222÷6=37（只）。鸡的数量是37+26=63（只）。

答：兔的数量是37只，鸡的数量是63只。

笼子里有21只蛐蛐和30只蝈蝈。红毛精灵每变一次，会把其中的2只蝈蝈变成1只蛐蛐;绿毛精灵每变一次，会把其中的5只蛐蛐变成2只蝈蝈。两个精灵一共变了15次后，笼子里就只有蝈蝈而没有蛐蛐了。这时蝈蝈有多少只？

两个精灵变化方式不同，而且有两种动物，比较难做。

找数据，逐步假设：最后没有蛐蛐，是被绿毛精灵给变没了。因为绿毛精灵每次会变没5只蛐蛐，那么蛐蛐的最大数目（经过红毛精灵变化后）必然是5的倍数。

原先是21只蛐蛐，那么经过红毛精灵的变化，蛐蛐总数可能为25，30，35。不可能大于等于40只，因为若达到40只，红毛精灵得变化19次，但是总的变化次数只有15次。

1.若为25只蛐蛐，则红毛精灵变化4次，绿毛精灵变化5次。加起来才9次，不符合题中的15次。

2.若为30只蛐蛐，则红毛精灵变化9次，绿毛精灵变化6次。加起来为15次，符合题意。

3.若为35只蛐蛐，则红毛精灵变化14次，绿毛精灵变化7次。加起来是21次，不符合題意中的15次。

所以，蝈蝈有30-9×2+6×2=24（只）。

把两位精灵变蛐蛐的过程列表。

绿毛精灵多变一次，蛐蛐就少6只，直接跳跃到最后减少21只蛐蛐，变化了6次。15-6=9（次），红毛精灵变了9次。

根据次数求蝈蝈：30-9×2+6×2=24（只）。

训练一二一

笼子里有30只蛐蛐和30只蝈蝈。红毛魔术师每变一次，会把其中的4只蝈蝈变成1只蛐蛐;绿毛魔术师每变一次会把其中的5只蛐蛐变成2只蝈蝈。两个魔术师一共变了18次后，笼子里就只有蝈蝈而没有蛐蛐了。这时蝈蝈有_____只。（答案见下期）

上期答案：1.老师有24支笔，奖给了4名“三好学生”。

2.20名同学，192棵树苗。