面向高光谱图像的高斯-稀疏子空间聚类算法

龙咏红

（广东工业大学应用数学学院，广东广州510520）

高光谱图像（HSI）的每个像素含有丰富且连续的光谱特征［1］。在图像分类中，监督分类是需要标记的训练样本，然而在高光谱图像，训练样本是未知的。因此，在聚类任务中，应用更广泛的是无监督聚类，传统的无监督聚类方法有K-means聚类和模糊聚类、子空间聚类等。图像分类的目的是为了更好地分割图像中的目标事物，例如地面、树、建筑等。面向高光谱图像进行分类的算法层出不穷，如基于领域约束的［2］、基于新进化群的模糊聚类［3］、基于子空间聚类的［4-6］。然而，高光谱图像是高维的数据，它包含从可见光到红外波段的数百个相邻的窄光谱波段。高维数据的多特征所带来的高维诅咒会明显降低算法的收敛速度［2］和图像聚类的精度［7］。因此，很多研究高光谱聚类的学者提出各种改进的方法来缓解传统算法应用在高维数据上的维数灾难。在文献［3］中，Ghamisi P等提出的进化模糊聚类算法，是结合分数阶达尔文粒子群优化［8］的模糊聚类，克服了高维数据问题所造成模糊均值聚类的收敛数据较慢和在具有多个局部最优的复杂问题下，粒子群优化算法可能会失败的问题。然而这种进化的模糊聚类算法不包括高光谱图像的空间和相邻像素的上下文信息，只考虑光谱信息；在文献［2］中，Li S提出的领域约束的聚类算法在聚类的过程中，利用领域均匀性指数度量空间信息并与光谱信息结合利用自适应距离标准进行聚类，领域约束克服了随着领域空间的维度增加，领域的样本数量也随之增加，以及所涉及的计算成本也不断增加的问题，同时这种方法再生成领域均匀性指数时需要足够已有标签的示例，往往在实际应用中，获取足够的标签数据是困难的且耗费成本高。

在高维数据的聚类算法当中，子空间聚类是实现高维聚类的有效途径。子空间聚类包含稀疏子空间聚类和低秩子空间聚类。然而，在聚类高光谱图像时，稀疏子空间聚类算法聚类高光谱图像时只利用到了图像的谱信息，而忽视了图像的空间信息，使得图像分类的精度降低了。为了提高聚类精度，提取到更多的像素点信息，结合高光谱图像的光谱信息与空间信息对图像进行子空间聚类的研究方法不断涌现［4-6］。

目前面临的最大挑战是如何克服高维问题和充分提取复杂的光谱信息和空间信息的联系，实现高光谱图像聚类精度的提高与聚类模型的鲁棒性。面向高光谱图像基于子空间聚类的算法聚类的关键是谱聚类，然而谱聚类的关键是构建相似度矩阵。稀疏子空间聚类是由稀疏系数矩阵构建相似度矩阵，只考虑到了每个像素点的光谱信息，却忽略了它们之间的空间信息，而且稀疏子空间聚类的模型，只对像素点做了稀疏约束，忽略了它们之间的相似性，不能完全作为分组的依据。如前所述，为了充分提取更多的空间信息与光谱信息，我们在稀疏子空间聚类的基础上，提出两个新的构建相似度矩阵的方法。方法的启发来自文献［4］，提出的一种计算稀疏系数矩阵列向量之间的余弦值与计算像素点之间的欧式距离来构建谱聚类的相似度矩阵，利用了光谱信息与空间信息进行聚类，虽然聚类的精度相对经典的聚类算法有所增长，但是增长幅度太低。首先，文献［4］利用欧式距离来度量高维稀疏数据的相似性不是一个很好的选择［9］，在计算相似度时不能完全搜索到像素间的空间上下文信息；其次，选择的稀疏模型会被异常像素干扰。因此，我们在重新选择子空间聚类模型的基础上，清除了异常像素的干扰后，利用PCA提出像素点的主要特征，再由高斯核函数计算它们之间的相似性，可以搜索到高光谱图像的空间上下文信息，最后构造图的相似度矩阵，利用谱聚类得到聚类结果。经过大量实验，本文算法较大程度地提高了高光谱图像的分类精度。

1 相关工作

1.1 稀疏子空间聚类

稀疏子空间聚类高光谱数据是基于谱聚类完成的，它的基本思想是高维空间的像素数据可以在低维空间中进行稀疏表示，由凸优化解得的稀疏表示构建相似度矩阵，能更好地体现像素数据子空间的属性，并且具有稀疏性，最后利用谱聚类得到聚类结果。

以下介绍稀疏子空间聚类的框架。为了减少异常像素点的干扰，我们重新选取稀疏子空间聚类的模型。文献［10］提出了含噪声与异常值的两个稀疏子空间聚类模型，我们利用这两种稀疏子空间聚类模型，获得涵盖大量光谱信息的稀疏系数矩阵。高光谱图像的像素数据集IM×N×D是3维的，M、N、D分别是高光谱图像的长、宽、波段，对像素I按波段D列化成MN×D的高光谱像素数据矩阵Y=｛y1，y2，…，yMN｝，yi∈RD。假设存在n个仿射子空间，每个仿射子空间的维数为，往往子空间的个数与维度是很难确定的，一般的，我们也是选取自身作为字典矩阵，并且取自表示的稀疏表示为零，避免自表示。实际应用的高光谱图像，维度有100个波段以上，为了减少计算复杂度与运行时间，同时又能减少冗余的信息，在实验前利用主成分分析（PCA）进行降维处理，把D个光谱特征提取出d（d≤D）个主成分特征，得到新的数据集矩阵 Z=（z1，z2，…，zMN），Z∈Rd×MN，由 Yan Q［4］的实验结果可以看到，图像中存在少量的被噪声污染的像素，含噪声模型可表示为

其中，C为稀疏系数矩阵，E为噪声矩阵。

由式（1）通过凸优化求得像素点的稀疏系数矩阵 C=［c1，c2，…，cMN］∈RMN×MN，然后标准化稀疏系数矩阵的每一列向量。

求解得到系数矩阵C后，由系数矩阵计算求得如下相似度矩阵

最后，数据的聚类结果由规范化分割算法对相似度矩阵W进行谱聚类获得。

因此，稀疏子空间聚类是利用稀疏系数矩阵构建谱聚类的相似度矩阵的。稀疏子空间的聚类算法步骤如下：

（1）输入像素数据集 Y∈RMN×D，n 个子空间；

（2）根据稀疏子空间聚类模型（1），利用获得的像素数据计算稀疏系数矩阵C；

（4）由C构建谱聚类的相似度矩阵W=│cij│+│cji│；

（5）利用基于Normalized Cut准则的谱聚类得到聚类结果。

1.2 余弦-欧式相似度矩阵和余弦动态相似度矩阵

文献［4］聚类高光谱图像的主要思想是通过结合光谱信息与空间上下文信息构造新的相似度矩阵，最后利用标准化分割聚类高光谱图像，克服稀疏子空间聚类只考虑到了光谱信息而忽略了空间信息的问题。

面向高光谱图像基于子空间聚类的算法关键步骤是光谱聚类，然而谱聚类的关键是构建相似度矩阵。在SSC的基础上，利用式（1）求得如下稀疏系数矩阵

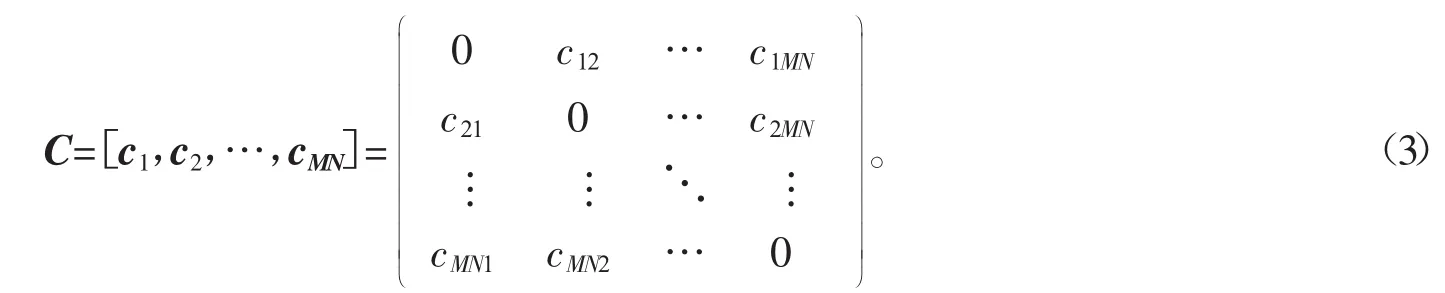
稀疏系数矩阵 C=｛c1，c2，…，cMN｝，ci∈RMN，把 ci定义为稀疏表示向量［11］，是每个高光谱像素被其他像素线性表示系数，可以用它们的余弦值来度量HSI像素之间相似性，它携带了丰富的高光谱像素的光谱信息，同时求得的余弦值提取了高光谱图像的空间结构信息。假设ci和cj是数据zi与zj的稀疏表示向量。在理论上，若zi与zj相似，则可以认为稀疏表示向量也是相似的。获得稀疏表示向量余弦值如下

其中，稀疏表示向量的余弦值是属于［0，1］的。

只考虑高光谱像素的光谱信息，对于高光谱图像聚类往往是不够的，因此在提取像素的上下文信息上，Yan Q［4］是通过计算每个像素点的欧式距离来提取。高光谱像素间的距离公式为

并结合稀疏表示向量的余弦值构造图的相似度矩阵，定义为Cosine-Euclidean相似度矩阵，构造模型为

高光谱图像的形成受很多因素的影响，但是具体哪个因素影响严重我们不得而知，所以Yan Q［4］在以上想法基础上再升华这一想法，给两者加个动态权重，即

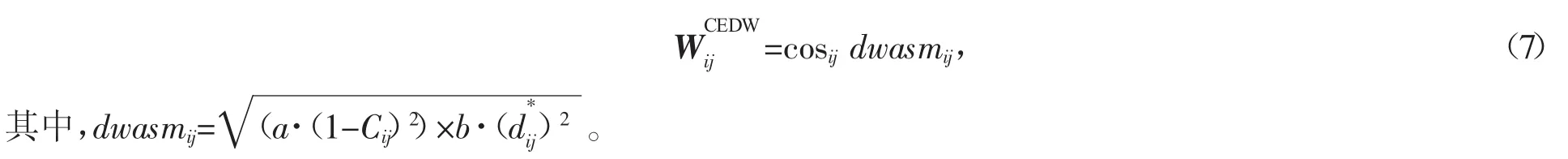
最后，通过谱聚类得到聚类结果。

2 PGKC算法

本文的想法源于文献［4］，Yan Q提出稀疏表示向量的每一列代表着每个像素点被其他像素点的线性表示，可以用余弦角度来测量它们之间相似性，稀疏表示向量包含大量高光谱图像的光谱信息，并结合像素点的欧式距离来提取每个高光谱像素点的空间信息，构造了不同形式相似度矩阵。两者的结合是光谱信息与空间信息的结合，最后通过谱聚类得到分类结果。实际应用中，高光谱遥感影像的每个像素点往往有着上百个光谱波段，这就意味着每个像素点有上百个特征，高维空间中数据较低维空间中数据分布要稀疏，其中数据间距离几乎相等是普遍现象，因此在高维空间中无法基于距离来构建高光谱像素的相似度，更重要的是，Yan Q选择计算稀疏表示向量的模型受异常像素样本的影像干扰，使得提取的光谱信息不充分，从而导致聚类精度偏低。

2.1 PGKC算法框架的构建

本文利用以上稀疏模型，求出包含大量光谱信息的稀疏系数矩阵，在文献［4］的基础上构造两种相似度矩阵，利用高斯核函数计算经过特征提取后的像素点的相似度，克服了在高维数据中利用欧式距离度量稀疏像素点的相似性是几乎失效的问题，同时也简化了计算，减少了计算的成本。在给定惩罚项条件下，结合稀疏系数矩阵的稀疏向量余弦值与像素点间的相似性构建谱聚类的相似度矩阵。

相比一般的利用欧式距离来计算两像素点的相似性，往往核函数用的更广泛，我们利用高斯核函数来度量两个像素点的相似性，能够提取出更高的空间结构信息。任意取两个像素点zi和zj，它们的高斯函数的相似性度量为

显然，Qij属于［0，1］的范围，是度量像素间相似度的不错选择，再结合像素点稀疏表示向量的余弦值，构造的相似度矩阵可以表示为

其中，cosij是由式（4）计算得到的。为了满足谱聚类中无向图的相似度矩阵的对角元素为零的条件，这里取对角为零，并且。

最后将构建的相似度矩阵应用在标准化分割的谱聚类上，可以得到图像的聚类结果，本文将以上聚类算法命名为PGKC算法。

本文主要的特色可以分为两点：首先利用主成分分析提取出像素点的最大的特征信息，筛选出冗余信息，再用高斯核函数计算出每个像素点的相似性，克服了在高维数据中，直接利用欧式距离度量稀疏像素点的相似性是几乎失效的问题；更深远的，PGKC模型计算出的相似度矩阵中携带了大量光谱信息与空间信息，从而提高了高光谱图像的聚类精度。

PGKC的算法步骤如下：

输入：HSI：I∈RM×N×D，n 类别；

（1）将 3-维的 HSI像素数据集转换成 2-维的数据集 Y=｛y1，y2，…，yn｝∈RMN×D；

（2）利用 PCA 提取 HSI像素的最大特征信息，得到新的 HSI像素数据集为 Z=｛z1，z2，…，zd｝∈RMN×d；

（3）根据稀疏子空间聚类模型（1），利用获得的像素数据计算稀疏系数矩阵C；

（5）由式（4）和（8）分别求出稀疏表示向量的余弦值cosij与Qij高斯核函数；

（6）利用式（9）计算像素的相似度矩阵WPGKC；

（7）最后利用基于Normalized Cut准则的谱聚类得到聚类结果。

输出：HSI像素的聚类结果。

3 实验与结果分析

3.1 实验数据

我们通过大量实验来证明本文提出的方法比其他先进的方法聚类高光谱图像的性能更好。以K-means、稀疏子空间聚类［10］（SSC）和模糊聚类［12］（FCM）、先进算法的 CE 和 CEDW［4］这 5 种聚类算法作为本文实验基准。

实验部分，我们选取两个高光谱数据集Pavia University影像和Pavia Centre影像作为实验数据集，可以在网址（http://alweb.ehu.es/ccwintco/index.php?title=Hyperspectral_Remote_Sensing_Scenes）上下载。Pavia University是610×610的像素影像，有103个光谱波段，它的地面真值有9个不同的类别。Pavia Centre是1 096×1 096的像素影像，它的地面真值有8个不同的类别。Pavia University和Pavia Centre地面真值如图1所示，Pavia University影像和Pavia Centre影像的基本特征如表1所示。

图1 Pavia University影像和Pavia Centre影像的地面参考图

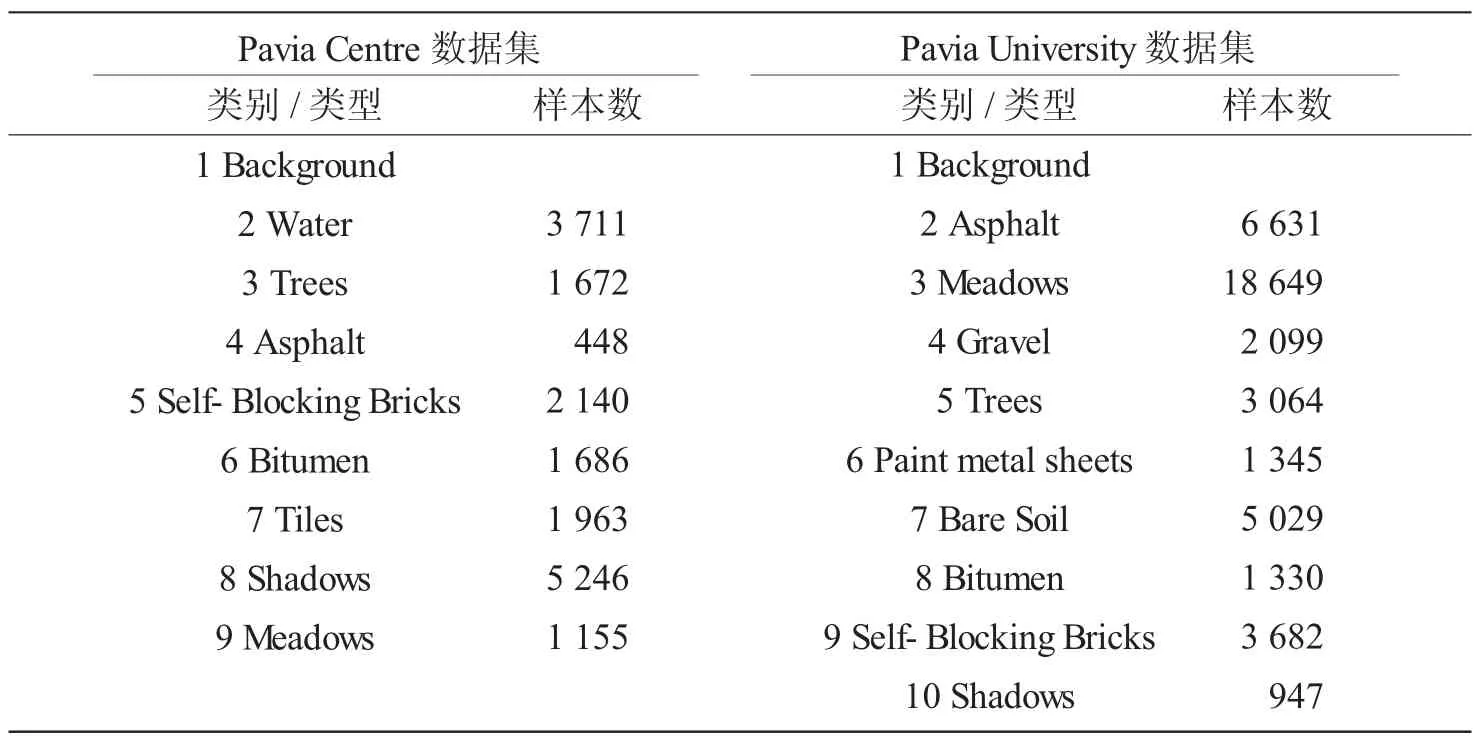
表1 Pavia Centre和Pavia University每个类别的样本数量

3.2 评价指标

利用 kappa系数（KC）、总体精度（OA）、用户精度（UA）、制图精度（PA）、平均聚类精度（AA）［13］来评价本文方法聚类高光谱图像的性能，并和传统的聚类方法K-means、FCM［12］、SSC［10］以及最近提出的CE与CEDW［4］进行比较。SSC方法的代码可以通过网址（http://vision.jhu.edu/code/）查询。

3.3 实验结果分析

3.3.1 Pavia Centre影像的实验结果分析

首先，我们的算法用于Pavia Centre影像，实验运行的结果与K-means、稀疏子空间聚类（SSC）、模糊聚类（FCM）、CE和CEDW这些算法进行比较分析。从图2可以看到这些方法对Pavia Centre影像的聚类效果，可以清晰地看到我们的算法PGKC的可视图要比这5种算法的聚类效果要更好、更具体，在类别 Water、Self-Blocking Bricks、Bitumen、Tiles、Shadows、Meadows上的可视图要更接近地面真值。本文提出的算法和其他算法的聚类性能评价分析如表2所示，我们利用总体精度与平均精度、kappa系数来评价算法的聚类性能；从表2中我们可以看到本文算法应用在Pavia Centre影像上聚类精度kappa系数、总体精度与平均精度达到最大值，它的总体分类精度（OA）达到了最高为87.33%，对应的Kappa系数分别为0.846 8。相比算法CE和CEDW分别增长了38.66%和26.35%，KC分别增长了0.443 5和0.317 8。

图2 5种算法与PGKC算法在Pavia Centre影像上实现的聚类结果图

表2 Pavia Centre scene数据集的总体精度和平均精度、Kappa系数

更细节的，从表3可以看到每个类别的聚类精度分布情况，其中类别Water、Self-Blocking Bricks、Bitumen、Tiles、Shadows、Meadows应用我们算法的制图精度较其他5种算法的在相应类别的聚类精度相对要高，有的类别达到了 100%。其中类别 Water、Self-Blocking Bricks、Bitumen、Tiles、Shadows、Meadows根据我们提出的算法PGKC获得的制图精度与地面参考图是几乎相符合的。

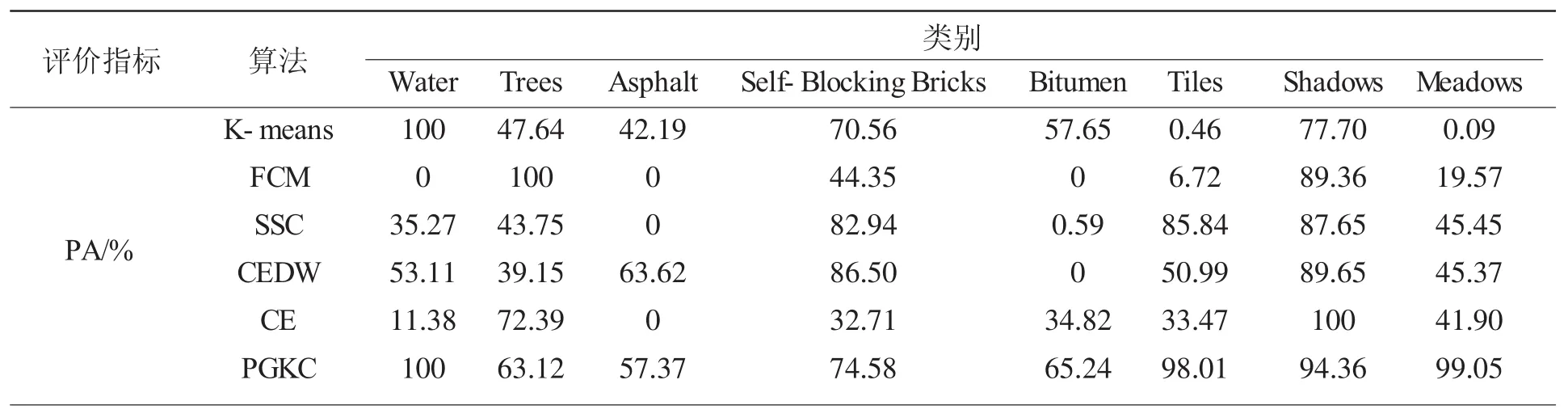
表3 Pavia centre数据集中每个类别的用户精度与制图精度

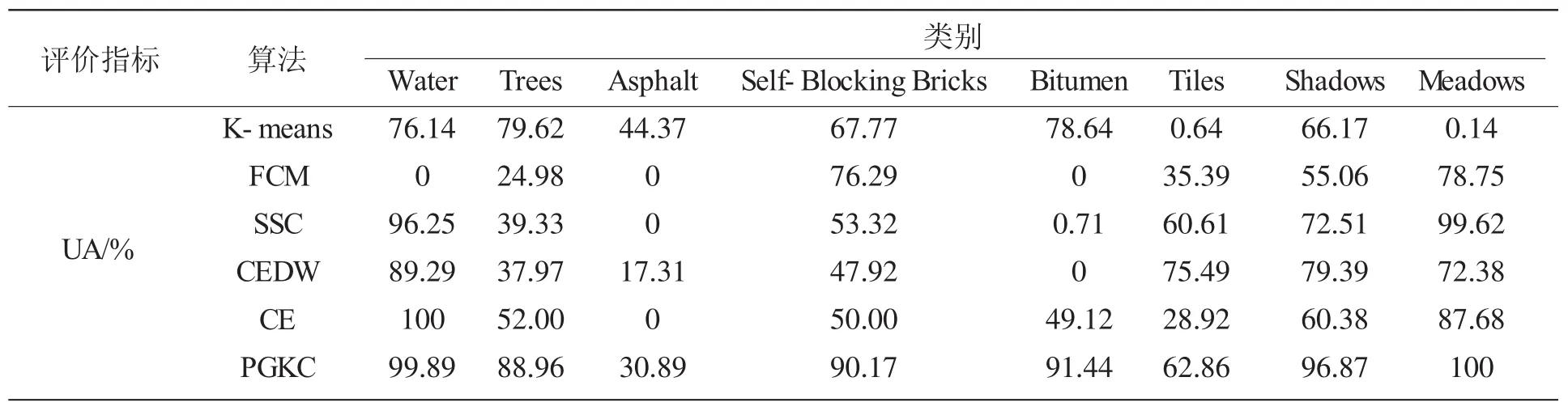
续表

我们提出的算法相对5种聚类算法的聚类精度是最高的，增加的精度也是显著的。聚类效果比5种算法优越的原因主要是由于我们的算法在最开始就对HSI像素数据进行了特征提取，删除了冗余的信息，同时在接下来的实验当中选择的稀疏模型可以避免异常像素的干扰，使得用于后面的实验计算中不仅可以利用稀疏表示向量的余弦值度量像素的光谱相似性，而且可以利用高斯核函数度量像素的空间相似行，所以我们的算法充分利用到了HSI像素丰富的光谱信息与空间信息。

3.3.2 Pavia University影像的实验结果分析

紧接着，将我们的算法应用在Pavia University影像上。我们的算法PGKC与5种算法聚类的Pavia University影像的视觉效果图可以从图3看到。我们可以清晰地从表4看到，本文PGKC算法在Self-Blocking Bricks上的制图精度（PA）是最高的，在Shadows的用户精度达到100%。最后，从表5看到，我们提出的算法总的聚类精度OA和Kappa系数是最高的，分别为62.30%、0.510 6，而算法K-means、CE和SSC的OA是最低的，分别为48.60%和51.15%、51.24%。我们提出的算法是提高了在算法SSC和CE的精度，这是由于SSC算法只考虑了HSI像素的光谱信息却没有考虑到它们的空间信息，而CE算法虽然光谱信息与空间信息都考虑到了，但是CE算法包含的空间信息较弱。

相对的，PGKC算法较CE和CEDW算法OA增长了11.92%和11.05%，KC增长了0.193 9和0.104 8。这说明我们的算法比算法CE和CEKW要优秀，明显减少了算法CE和CEDW的错误率。我们的算法得到了最好的视觉效果图和更高的聚类。特别的Pavia University影像中类别Self-Blocking Bricks精度相对其他方法得到大幅度提高，如表4所示。因此，KC、AA和OA值证实我们提出的算法聚类性能比其他算法要更好。

图3 5种算法与PGKC算法在Pavia University影像上实现的聚类结果图

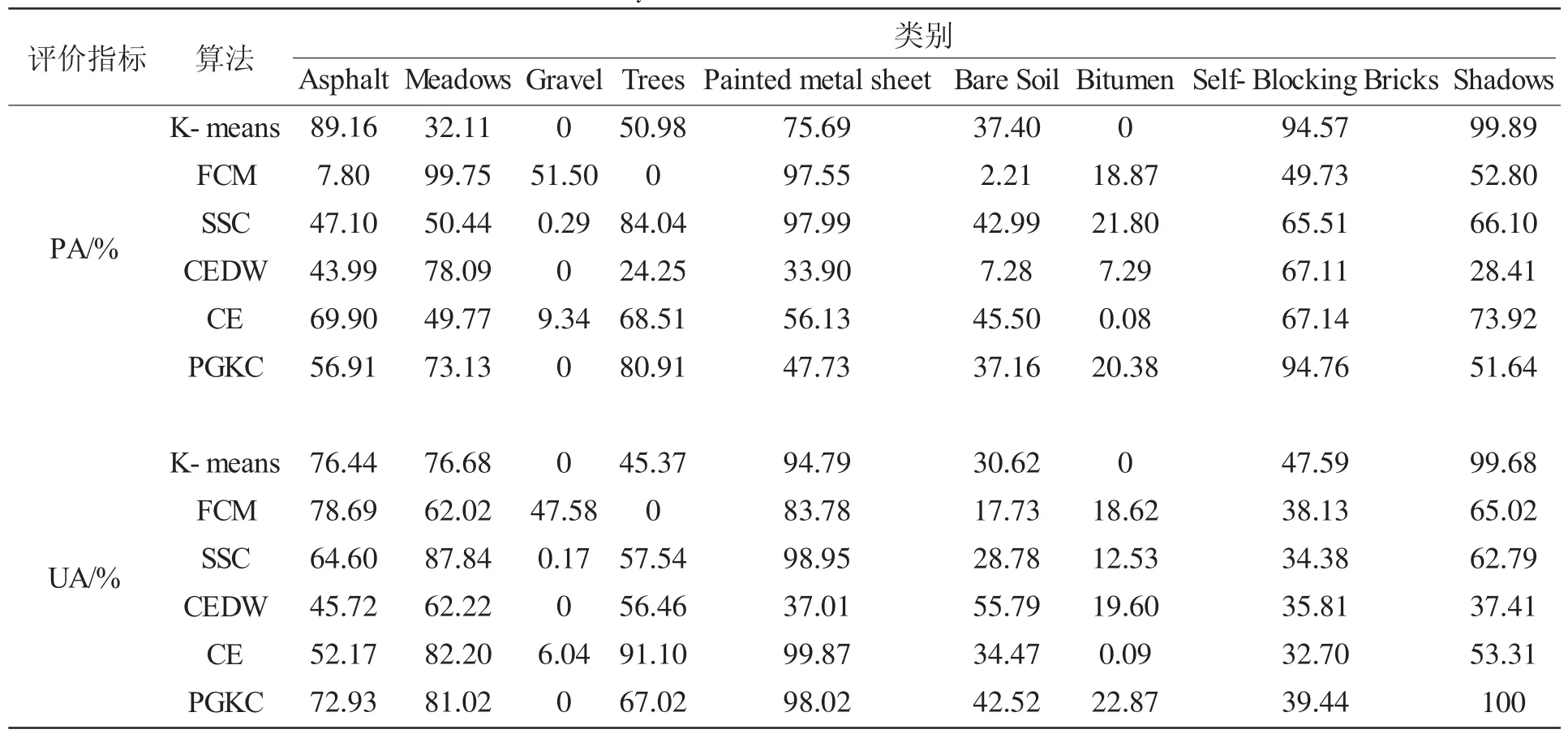
表4 Pavia University数据集的每个类别的用户精度与制图精度

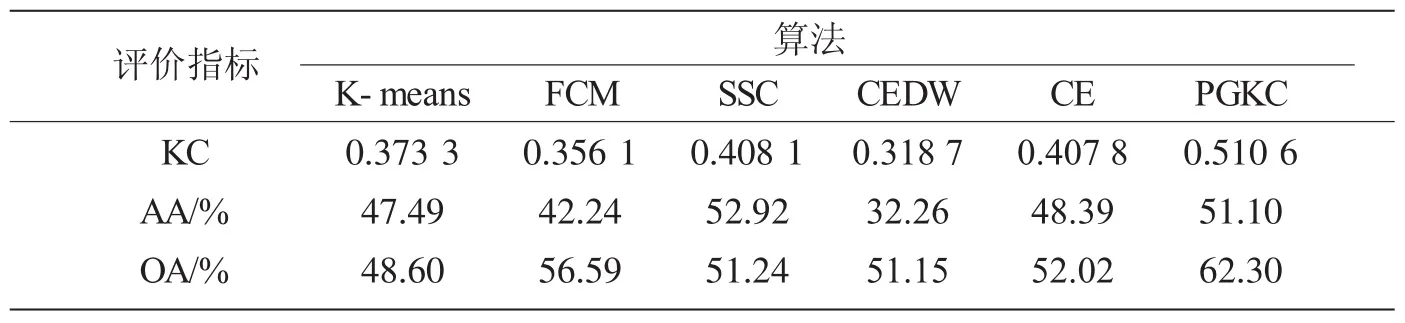
表5 Pavia University数据集的总体精度和平均精度、Kappa系数

4 结语

本文在文献［4］的基础上做了一个提升，在SSC模型和利用HSI的空间信息两个方面做的提升之后，选择可以避免异常像素干扰的稀疏模型求得的稀疏表示向量度量像素的光谱相似性，减少了错误分类率；然后利用特征提取后像素的高斯核函数度量空间相似性。在此基础上，提出一种构造相似度矩阵的方法，这种方法充分利用到了高光谱像素的光谱相似性和空间相似性，克服了算法CE和CEDW中异常像素干扰造成分类错误偏高的问题和利用空间信息的不足，增强了图的邻接矩阵的连通性，从而提高了分类精度。经过大量实验证明，相比其他先进的算法，本文提出的算法应用在Pavia Centre和Pavia University两个影像上，实现了更好的性能。