矩形顶管施工参数对变形的影响研究
2020-11-19贾远航朱正国
贾远航, 朱正国,2, 丁 祥
(1.石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室,河北 石家庄 050043;2.河北省金属矿山安全高效开采技术创新中心,河北 石家庄 050043;3.中铁第五勘察设计院集团有限公司,北京 102600)
顶管法是继盾构法之后一种重要的非开挖施工方法,其特殊的施工工艺可以达到对地表少开挖、小开挖的效果,对城市的环境起到很好的保护作用。与盾构法相比,顶管法具有节省材料、缩短工期、占地面积小、公害少、造价低等优点[1]。目前研究主要集中在通过理论分析、现场监测、数值模拟等手段分析顶管施工对周围土体的影响,未见针对矩形顶管施工中的工作参数进行的相关论述。本文在查阅大量顶管工程相关资料的基础上,以河北南部电网某电力隧道为背景,通过FLAC3D有限差分软件建立矩形顶管隧道的数值仿真模型,研究矩形顶管施工参数对变形的影响。
1 仿真模型的建立
1.1 建立模型
本文建立的数值仿真模型见图1。矩形顶管隧道的截面尺寸取为6.0 m×4.8 m,为消除边界效应的影响,垂直隧道轴线方向、隧道底部至模型底部取开挖轮廓的3~5倍,隧道埋深按照实际埋深取为4.5 m,隧道轴线方向取60 m,模型在x、y和z三个方向的整体尺寸为66 m×60 m×28 m。模型中的顶管机外壳、顶管管节厚度分别取为0.1 m、0.5 m,顶管机、管节长度分别取为3.0 m、1.5 m。
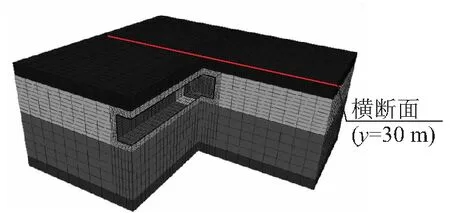
图1 整体模型
顶管隧道施工过程中主要的结构物有顶管机、管节及注浆层。为模拟大刚度顶管机对土层的支撑作用,顶管机的弹性模量取210 GPa,密度取7 850 kg/m3,泊松比取为0.3。顶管管节采用C50钢筋混凝土,由于管节之间的连接会造成一定的刚度折减,因此本文是按照0.8的折减系数进行取值,取弹性模量为27.6 GPa,泊松比取为0.2。
1.2 顶管过程模拟
顶管顶进过程中主要通过空单元及刚度迁移法来实现土体开挖及管节顶进的全过程,具体的施工过程如下:
(1)按照表1中给定的土层分布情况对各土层赋予相应的参数,然后进行计算以生成矩形顶管隧道的初始应力场、初始位移场,然后将模型产生的初始位移值清零。
(2)采用null单元将一个开挖步(1.5 m)要挖去的土体、顶管机外壳、矩形管节钝化。
(3)将顶管机外壳单元激活,模拟大刚度顶管机外壳对土层的强支护作用,在掌子面施加土仓压力,完成一个开挖步的施工。
(4)在第3个开挖步时给顶管机后方一个开挖步的土体施加注浆压力(由于顶管机长度按3 m考虑,此时0~1.5 m范围内将顶管机外壳部分钝化,认为此时顶管机通过该部分土体),按此步骤继续计算3个开挖步。
(5)第6个开挖步时,激活顶管管节、注浆层单元,此时,第1个顶管管节施工完毕。下一个开挖步时采用位移控制的方法,采用fish语言进行编程,将第1个顶管管节推进1.5 m并激活第2个顶管管节、注浆层。按以上步骤工进行45个循环直至所有管节顶进完毕。图2为施工全过程的示意图。
1.3 模型验证
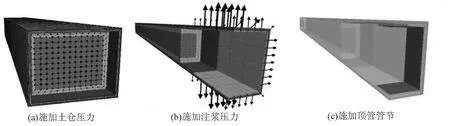
图2 施工过程示意图
Peck[2]教授通过大量分析地表沉降数据,于1969年提出地表沉降槽基本符合正态分布曲线的概念。在隧道周围土体不排水、体积不可压缩的前提下,认为隧道开挖引起的土体沉降主要是由土体损失引起的,即土体损失体积与地表沉降槽体积相等,据此得出了如下公式用于计算横向地表沉降:
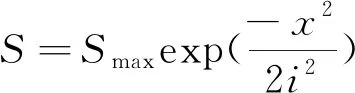
(1)
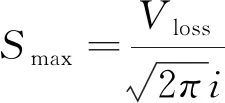
(2)
对公式(2)进行变换得到:
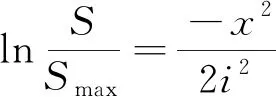
(3)
式中:S为任意点x处地表沉降值(mm);Smax为地表最大沉降值,一般为隧道轴线处地表沉降(mm);Vloss为隧道单位长度的土体损失量(m3/m);x为计算点距隧道轴线距离(m);i为沉降槽宽度(m)。
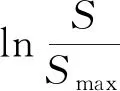
由图3可知,数值模拟计算所得数据均匀分布在拟合所得的直线周围,二者的线性相关系数R2=0.989 1。由此可知,本次数值模拟所得到的数据基本符合Peck公式,与其线性相关性较好。通过对数值模拟得出的土体沉降值与Peck公式的线性相关性分析验证了文中数值模拟方法的正确性。
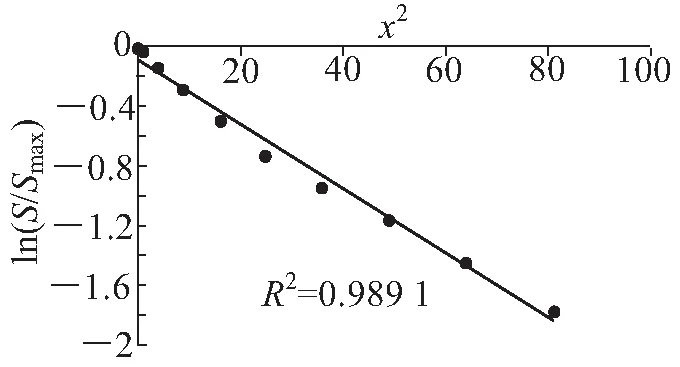
图3 y=30 m断面沉降拟合曲线
2 施工参数对地表变形的影响
2.1 顶管受力模式
顶管工程中土体受力模式如图4所示,顶管施工过程中土体受到的力主要有开挖面上的迎面阻力、顶管机外壳与土体间的摩阻力、注浆压力以及顶管顶进过程中管道与土体之间的摩擦阻力。
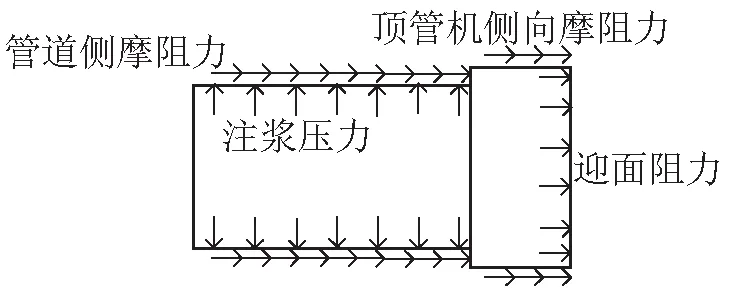
图4 矩形顶管工程土体受力模式示意图
由于矩形顶管施工过程中会持续注入触变泥浆,当注入的泥浆套饱满完整时可大幅减小管土间的摩阻力,为此本文进行相关分析时只考虑注浆压力与土仓压力,忽略摩阻力对变形的影响。
2.2 土仓压力对变形的影响
2.2.1 对掌子面变形的影响
由于土仓压力是直接作用于掌子面上的,当土仓压力发生变化时首先受到影响的就是掌子面。顶管隧道施工过程中土仓压力需要与顶管机刀盘前部的土体压力和地下水压力保持平衡,此时可以将掌子面变形控制在最合理的范围内。
由图5可知,当土仓压力小于0.1 MPa时,掌子面位移值为负值即由于开挖卸荷导致掌子面土体向开挖方向发生挤出变形。当土仓压力为0 MPa时,挤出变形最大值为29.61 mm,通过对掌子面的土体位移分析可知,该点位于掌子面中下部且掌子面后方6 m内土体损失量较大,该部分土体在卸荷作用下挤向隧道内部。当土仓压力为0.1 MPa时,掌子面最大位移值为1.68 mm,变形最大处位于掌子面上方,掌子面与未开挖时基本一致,位移值很小。此时土仓压力与掌子面前方土体侧向土压力值基本一致。当土仓压力大于0.1 MPa时,此时掌子面位移为正值即此时由于土仓压力的作用导致掌子面土体发生沿开挖方向的变形,挤压隧道正前方未开挖部分土体。土仓压力在0.1~0.3 MPa时变形曲线基本为直线,当土仓压力提升至0.4 MPa时掌子面变形值明显增加。随土仓压力的提高掌子面位移相比于上一工况变化值分别为31.27 mm、8.91 mm、9.97 mm、20.25 mm,变化量先减小后增加。
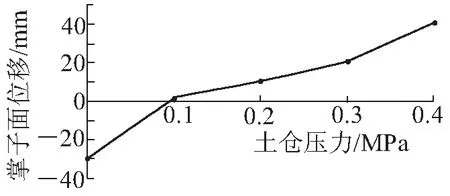
图5 不同土仓压力下掌子面纵向变形曲线
由图6可知,在掌子面上各点水平应力值随土仓压力增加而增加。当土仓压力为0 MPa时由于开挖造成的卸荷作用使得土体水平应力值迅速减小。当土仓压力为0.1 MPa时土体应力值先减小而后保持不变且始终小于等于未开挖时的土体应力值,在距离掌子面3 m距离处土体的水平应力值与未开挖时基本保持一致,其应力改变量为由于卸荷造成的土体应力值减小。当土仓压力大于0.1 MPa时土体水平应力值先增加后减小,即掌子面前方0~3 m土体应力值增加,距掌子面距离大于3 m后土体应力值开始逐渐减小,结合上文中掌子面上的位移情况,这主要是由于土仓压力对掌子面的挤压作用使得水平应力值增加。
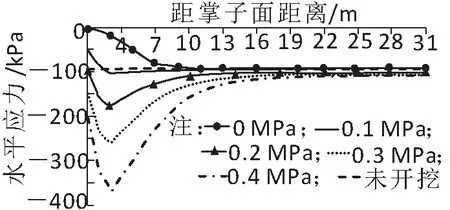
图6 不同土仓压力下掌子面前方土体水平应力曲线
土仓压力对掌子面前方的直接影响范围为0~3 m,该部分土体属于剪切扰动区,施工过程中受到开挖卸荷与施工应力的双重影响,当二者大小相当时土体应力值基本与未开挖时保持一致。距掌子面距离大于3 m处属于挤压扰动区,主要承受挤压应力而产生挤压变形,顶管机推进时挤压应力也随之增加,土体水平应力会有所增加。
2.2.2 对地表变形的影响
由图7可知,沉降槽基本符合正态分布形式,土仓压力越小沉降槽越深、曲线曲率越大。各工况地表处沉降最大值均发生在隧道中心处,顶管隧道的开挖对该点影响最大,随距离隧道中心距离的增加沉降值逐渐减小,当土仓压力增加时最大沉降量减小。土仓压力由0 MPa变化至0.1 MPa及由0.3 MPa变化至0.4 MPa时土体沉降值变化量较大,最大沉降值变化量分别为4.51 mm和3.06 mm,当土仓压力在0.1~0.3 MPa范围内沉降槽曲线基本未发生变化,土体最大沉降值变化量仅为1 mm。
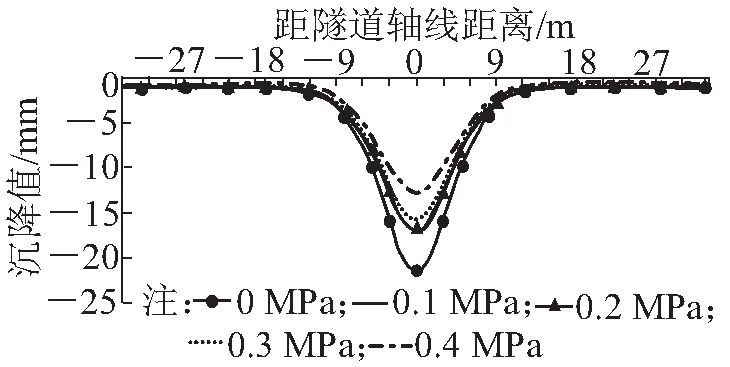
图7 不同土仓压力下地表横向沉降槽曲线
当土仓压力为0.1~0.3 MPa时地表处土体沉降量相对值虽不是最小的,但土仓压力增加相同数值的情况下地表处土体最大沉降值变化量相对较小,其最大变化量仅为1 mm;当土仓压力为0 MPa及0.4 MPa时地表沉降变化量相对较大,地表处沉降值对于土仓压力的敏感性较强。
由图8可知,各工况下沉降槽反弯点值分别为4.05 m、4.20 m、4.19 m、4.17 m、4.26 m,在土仓压力为0 MPa工况下沉降槽更深、更窄得到的沉降槽反弯点数值最小。当土仓压力为0.1 MPa时沉降槽宽度增加;0.1~0.3 MPa时随土仓压力增加沉降槽反弯点数值逐渐减小;当土仓压力为0.4 MPa工况时,沉降槽反弯点数值反而继续增加。
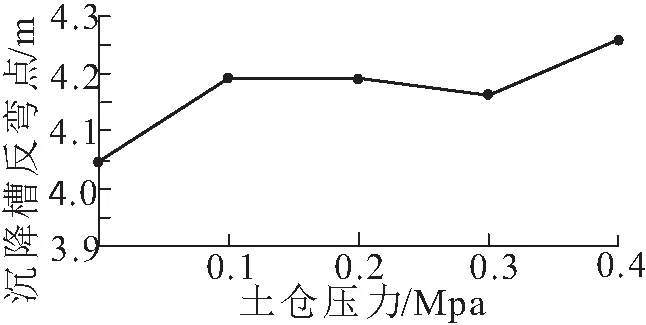
图8 不同土仓压力下沉降槽反弯点变化曲线
结合前述分析可知,本工程顶管隧道埋深较浅,在土仓压力作用下地表处发生隆起变形的可能性较大。地表隆起与地表沉降发生部位与原因有本质区别但二者又相互关联,顶管施工全程中由土体损失引起的沉降量应为地表隆起完成后发生的总沉降量,为实测沉降与隆起的总和[3]。
表1给出了不同土仓压力工况下的总沉降值,由该表可知,随土仓压力值增加地表沉降逐渐减小、隆起值逐渐增加,总沉降值先减小后增加。在顶管工程施工中应合理控制土仓压力值,保持土体总沉降值较小。
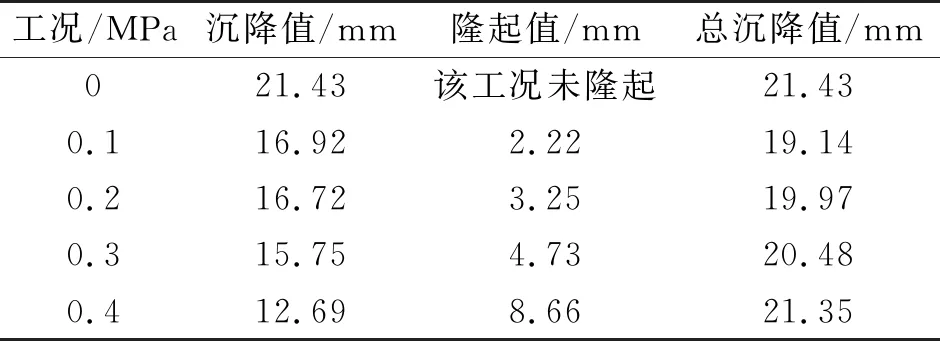
表1 不同土仓压力下土体总沉降
2.3 注浆压力对地表变形的影响
由图9可知,不同注浆压力工况下沉降槽曲线变化趋势基本一致,隧道轴线上方地表处沉降最大,随距隧道轴线距离的增加地表沉降值逐渐减小,沉降槽曲线基本符合正态分布。随注浆压力的提高土体最大沉降量不断减小,曲线变化趋势越来越平缓。
由图10可知,随注浆压力提高曲线沉降槽反弯点数值不断减小,各工况下沉降槽反弯点数值分别为4.32 m、4.22 m、4.10 m、3.82 m、3.50 m,相较于上一工况沉降槽反弯点数值分别减小了0.10 m、0.12 m、0.28 m、0.32 m。结合曲线斜率,当注浆压力小于0.11 MPa时沉降槽反弯点基本均匀变化,当注浆压力大于0.11 MPa时沉降槽反弯点减小速率明显加快。说明当注浆压力提高时能有效减小土体的横向影响范围,但是当注浆压力大于0.11 MPa后地表处开始出现隆起,开挖完成后的沉降槽反弯点数值虽然较小但是施工过程中隆起值较大。
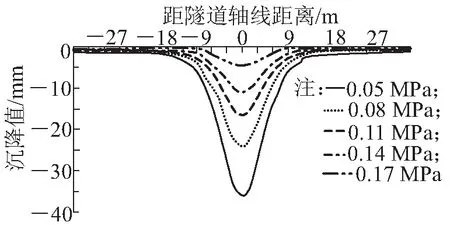
图9 不同注浆压力下地表横向沉降槽曲线
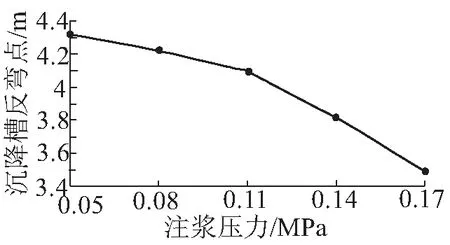
图10 不同注浆压力下沉降槽反弯点变化曲线
表2给出了不同注浆压力工况下总沉降值,注浆压力增加时沉降值减小、隆起值增加,土体总沉降值不断减小。因此,在施工中可以通过控制注浆压力值调整沉降值、隆起值使得土体总沉降值达到最小值以达到对顶管工程周围土体的保护作用。
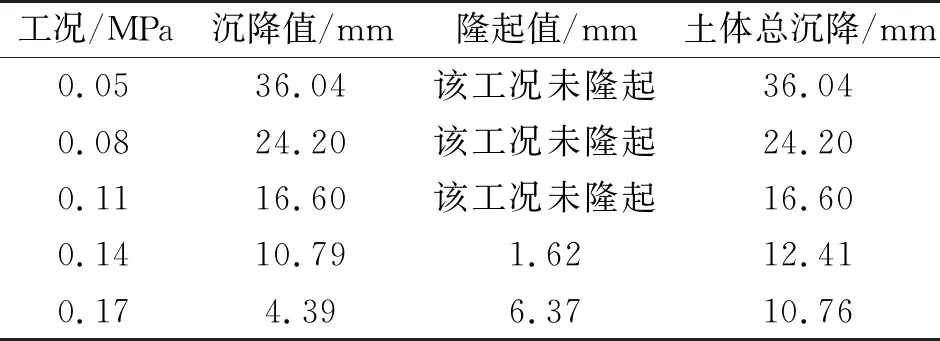
表2 不同注浆压力下土体总沉降
3 结论
(1)土仓压力对掌子面前方的直接影响范围为0~3 m,该部分土体属于剪切扰动区,受到开挖卸荷与施工应力的影响,当二者大小在数值上相当时土体应力值基本与未开挖时保持一致。
(2)土仓压力越小沉降槽越深、曲线曲率越大。随土仓压力值增加地表沉降逐渐减小、隆起值逐渐增加,土体总沉降值先减小后增加。在顶管工程施工中应合理控制土仓压力值,保持土体损失值较小。
(3)不同注浆压力工况下沉降槽曲线变化趋势基本一致,随注浆压力的提高沉降槽整体上浮,曲线变化趋势越来越平缓。注浆压力增加时沉降值减小、隆起值增加,土体总沉降值不断减小。
