基于模态分析的对称结构损伤识别法

李国庆 张 丽

(1.绍兴文理学院 土木工程学院，浙江 绍兴 312000；2.南昌大学共青学院 土木工程系，江西 共青 332020)

0 引言

结构在服役过程中因受到自然环境、荷载等诸多因素的影响，结构损伤在所难免，这就使得对早期的结构损伤识别尤为重要.在结构损伤识别方面国内外学者做了大量的研究，Cawley和Adams最早研究频率变化与结构损伤的关系[1].Pandey最早证明了损伤前后曲率模态可以用于损伤识别，即曲率模态法[2].Pandy和Biswas提出了基于柔度矩阵改变的结构损伤识别方法并应用到了多损伤状况[3]等.基于频率指纹发展起来的损伤识别方法只能对特定位置损伤识别，不能实现对整体对称结构的损伤识别[4-6],而柔度曲率矩阵变化率对对称结构的部分位置损伤识别结果不明显.本文将这两种方法的识别结果进行匹配，从而解决了各自的局限性，也实现了对整体对称结构的损伤识别，通过实例分析验证了此方法的可行性.

1 损伤识别的理论基础

1.1 正则化频率变化率

正则化频率变化率在整个区间上具有良好的单调性，有利于损伤的定位，最大的局限性在于此类方法不能实现对整体对称结构的损伤识别，在本文的算例中和文献[7]都体现了这一点.但是可以运用正则化频率变化率法对结构可能发生的损伤单元缩小范围，为下一步具体准确确定损伤单元提供了依据.

由文献[8]可知频率变化率与损伤的位置和程度有关，故频率变化率可表示为：

(1)

式(1)中：wui为损伤前的频率；wdi为损伤后的频率；r为损伤位置向量；ΔK为结构刚度变化量；ΔM为结构质量变化量；将fi在ΔK=0,ΔM=0处级数展开，并忽略高阶项，可得：

(2)

当式(2)中fi(0,0)=0时，结构处于无损状态，故可以表示为：

(3)

已知函数fi在ΔM=0和ΔK=0处偏微分为常数，因而式(3)可以表示为：

FFCi=ΔKmi(r)+ΔMni(r)

(4)

由于结构损伤对质量产生的影响很小可以忽略不计，即ΔM=0,所以式(4)进一步表示为：

FFCi=ΔKmi(r)

(5)

由文献[9]可知，正则化频率变化率(NRF,Normalized Change Ratio of Frequency)表示为:

(6)

从式(6)可以看出正则化频率变化率(NRF)只与损伤位置有关，所以可以运用正则化频率变化率对结构进行损伤定位.使用此方法对对称结构的损伤识别结果如图3所示，从图3中可以看出在只假设17号单元损伤的情况下，识别结果却显示出两个对称单元17和25都发生了损伤，出现了误判情况，故仅仅使用这一种方法不能实现对整体对称结构的损伤识别.接下来引入基于模态柔度矩阵推导出的损伤指标(RMDIAG)对这两个对称的疑似损伤单元进行进一步确认.

1.2 模态柔度曲率变化率矩阵

1.2.1 柔度矩阵

由模态分析可知，模态参数可以得到柔度矩阵表达式：

(7)

1.2.2 柔度曲率矩阵

将结构损伤前和损伤后的柔度矩阵分别表示为[Fu]和[Fd]，通过对柔度矩阵中的行元素使用式(8)和式(9)进行中心差分处理可以得到相应的损伤前和损伤后柔度曲率矩阵Cun×(n-2)、Cdn×(n-2).

(8)

(9)

1.2.3 柔度曲率矩阵差

基于文献[10]的思想，提出柔度曲率矩阵差的新表达形式为：

ΔC=Cd-Cu

(10)

式(10)中ΔC为柔度曲率矩阵的差；Cu为损伤前曲率矩阵；Cd为损伤后曲率矩阵.

1.2.4 模态柔度曲率变化率矩阵

基于文献[11]的思想，提出模态柔度曲率变化率矩阵(RM,Rate of change matrix of Modal flexibility curvature)的表达式：

RM=ΔC./Cu

(11)

式(11)中RM为模态柔度曲率变化率矩阵，(注意：式子中是点除，ΔC中的每个元素和Cu中每个元素对应相除).模态柔度曲率变化率矩阵(RM)进一步写成：

(12)

式(12)中hi,j为模态柔度曲率变化率矩阵(RM)第i行第j列元素，取RM对角线元素的绝对值，作为本文提出的损伤识别指标RMDIAG，即：RMDIAG=|diag(RM)|=[|h1,1|，|h2,2|，…，|h(n-2),(n-2)|]；

最后可以通过对比由正则化频率变化率识别出的两个疑似损伤单元的损伤识别指标值(RMDIAG)来确定最终真实的损伤单元，损伤识别指标值(RMDIAG)大的单元，即为真实损伤单元.下面通过算例验证了本文所提方法的可行性.

2 算例分析

以两端固定的单跨矩形截面梁为分析对象，梁长为6 m，截面尺寸为300 mm×500 mm，弹性模量为E=3.2×1 010 Pa，密度为ρ=2 500 kg/m3，泊松比0.3，使用ANSYS进行数值模拟分析，将整根划分为41个单元，单元结点编号1-42，单元编号1-41.单元的损伤通过调整弹性模量的大小来模拟，在使用正则化频率变化率进行损伤识别时，选取模态分析的前5阶频率.由式(7)可知，仅仅需要较少的模态参数就能得到理想的结构模态柔度矩阵，所以在使用柔度矩阵变化率曲率进行损伤识别时，选取模态分析的第1阶频率.两端固定的对称梁的模型如图1所示：

图1 单跨梁

2.1 正则化频率变化率对两端固定单跨梁的分析

依次令两端固定单跨梁的每个单元的刚度损伤10%、30%、60%，然后计算出每个单元在每种损伤情况下的前5阶频率，并代入(6)式中计算出各损伤情况下各阶频率下的正则化频率变化率NRFi，为了降低随机误差对损伤识别结果的影响，根据统计平均思想，取三种损伤情况下各阶的正则化频率变化率的平均值作为损伤定位指纹数据库，以单元编号为横坐标，以梁损伤时对应的平均之后的正则化频率变化率为纵坐标，做出曲线图，如图2所示.

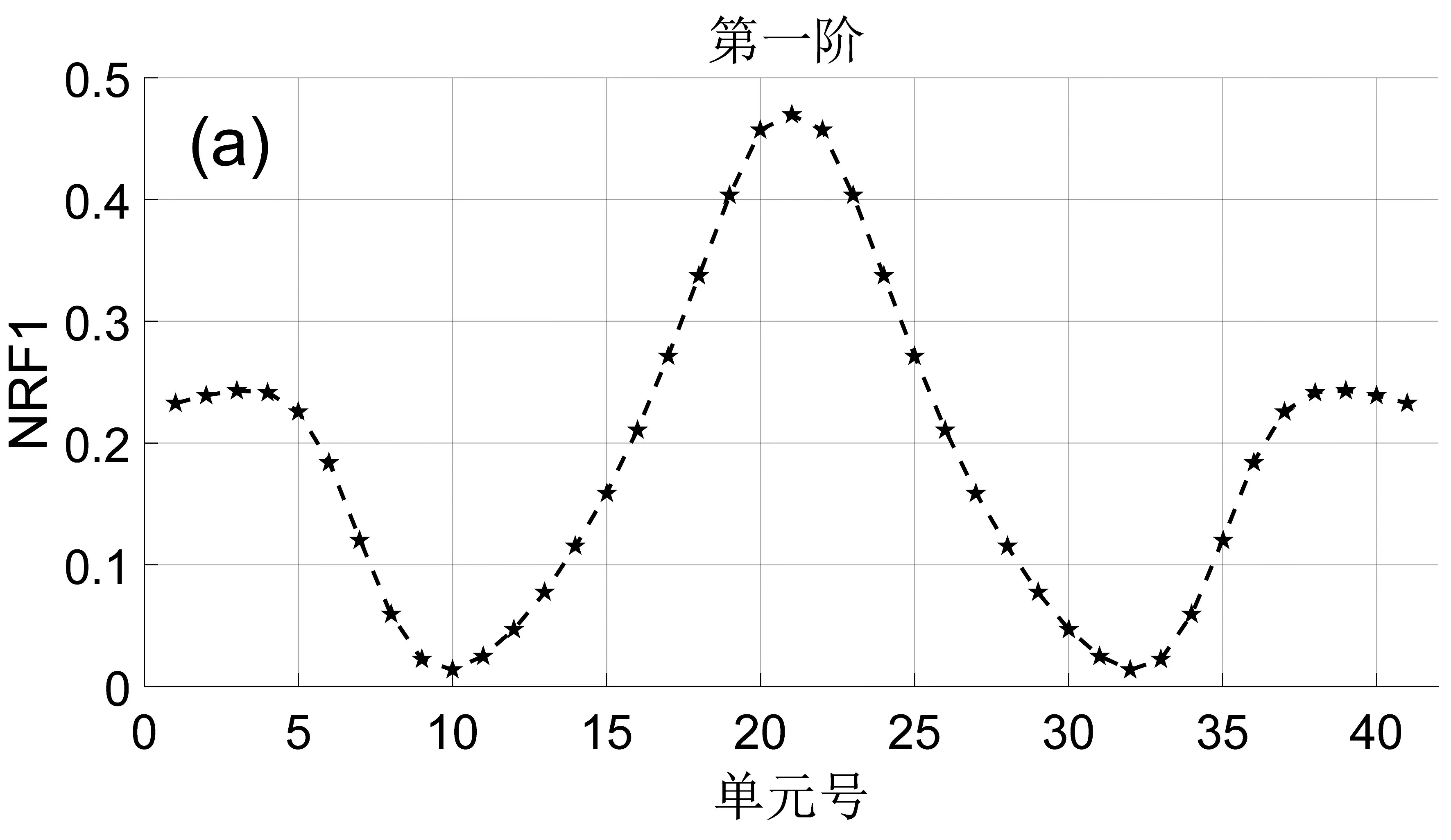
图2 不同损伤单元下梁的前5阶正则化的频率变化率

为了验证正则化频率变化率对两端固定对称梁损伤识别的局限性，假设17号单元刚度损伤30%，经过有限元软件ANSYS模态分析得到前5阶的模态参数.然后代入(6)式求出前5阶的正则化频率变化率为：NRF1=0.270 0;NRF2=0.258 5;NRF3=0.216 9;NRF4=0.209 6;NRF5=0.045 0;以这前5阶NRFi为纵坐标的值在各阶的频率指纹图上画一条水平直线，水平直线与曲线交点所对应的横坐标值为损伤单元的位置.损伤识别结果如图3所示.

从图3的各阶损伤定位图中可以看出17号单元和25号单元是损伤单元，在只假设17号单元发生损伤的情况下，但损伤识别结果却显示出两个对称的损伤位置，25号单元在没有损伤的情况下结果却显示发生了损伤，这就体现出了正则化频率变化率对结构对称梁损伤识别的局限性，只仅仅使用正则化频率变化率这一种方法不能够实现对整根结构对称梁的损伤识别.

图3 正则化频率变化率损伤定位结果

2.2 柔度矩阵曲率变化率对两端固定单跨梁的分析

梁单元损伤用其刚度系数降低来模拟，梁的单损伤分为三种工况为：工况1为第10号单元损伤30%、工况2和3为第17号单元分别损伤20%和60%.

以损伤指标值(RMDIAG)突变来表示损伤单元，由图4(b)和(c)损伤识别结果可以看出，对于两端固定单跨梁的同一单元在不同损伤识别工况下其损伤识别结果不同，从图4(b)可以看出17号单元刚度减低20%的情况下，损伤指标RMDIAG可以识别出损伤单元位置，但从图4(c)可以看出在17号单元刚度降低60%的情况下，损伤指标RMDIAG的识别结果看不出损伤单元的位置，在这种损伤情况下，需要根据图3正则化频率变化率损伤定位结果进行匹配，从图3正则化频率变化率损伤定位结果可以得到疑似损伤单元的位置有两个，分别是17号单元和25号单元，根据此识别结果就可以为下一步确定准确损伤单元位置缩小了范围，接下来只需要从图4(c)中对比17号单元和25号单元的损伤指标值RMDIAG，从图4(c)可以明显看出17号单元的损伤指标值RMDIAG明显大于25号单元的损伤指标值RMDIAG，说明17号单元是损伤单元，这与假设损伤工况相同，证明了此损伤结识别果非常理想.在识别不出损伤单元的情况下将两种损伤识别的方法的损伤识别结果相匹配，这样可以大大减少损伤识别的误差，从而提高了损伤识别的精度.也验证了本文所提出的将两种损伤识别结果进行匹配的方法是可行的.

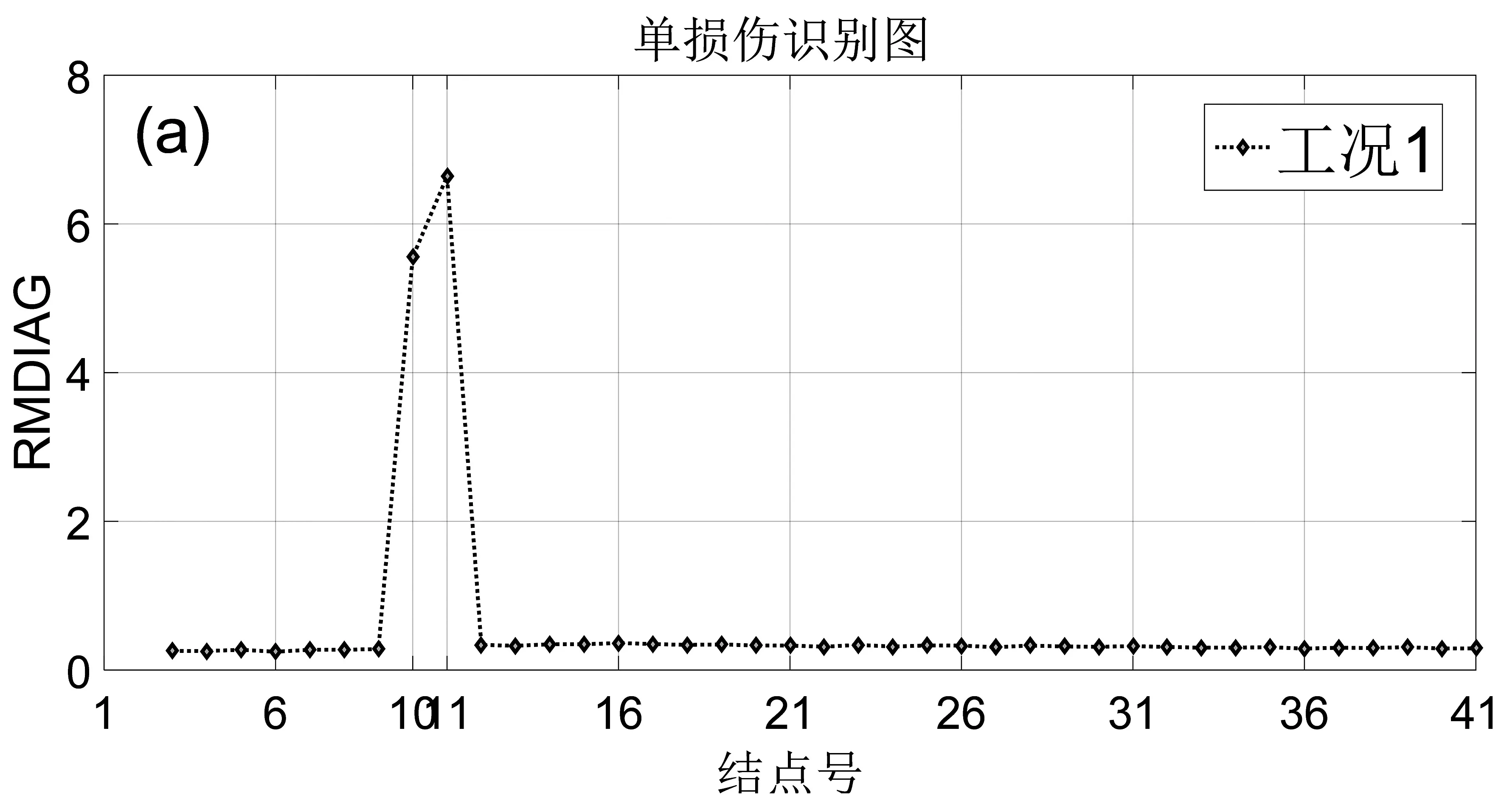
图4 单损伤识别结果

3 总结

(1)正则化频率变化率在整个区间上具有良好的单调性，有利于损伤的定位，缺点在于识别结果为两个对称的损伤单元，不能实现对整体对称结构的损伤识别.

(2)本文通过对柔度矩阵中元素进行中心差分处理，推导出了新损伤指标(RMDIAG)，并应用于算例分析，结果表明，该指标对部分单元损伤识别结果可以，但对个别单元在不同损伤情况下损伤识别结果不明显.

(3)通过上述的算例分析验证了本文所提方法的可行性，针对对称结构损伤识别的原理大致分为两步：第一步，首先通过正则化频率变化率对对称结构进行损伤定位分析，识别的结果为两个对称的疑似损伤位置，为下一步准确识别真实损伤单元缩小了范围.第二步，使用本文基于柔度矩阵推导出的新损伤指标值(RMDIAG)对两个对称损伤单元进行比较，损伤指标值(RMDIAG)较大的单元，即为真实损伤单元.本文所提的方法可以使损伤定位更加精确，同时也解决了各自对损伤识别的局限性，此方法为对称结构的单损伤识别提供了新思路.