奇异值分解在遥感图像数据压缩中的应用
2020-11-19陈文青
陈文青 范 恩 胡 波
(1.绍兴职业技术学院 信息工程学院, 浙江 绍兴 312000;2.绍兴文理学院 计算机科学与技术系, 浙江 绍兴 312000;3.宁波气象局, 浙江 宁波 315012)
0 引言
随着互联网普及和社会数字化转型,数据规模向PB级(PB指petabyte,PB是数据存储容量的单位,1PB=1024TB,1TB=1024GB,1GB=1024MB)发展,数据种类繁多,有各种结构化、半结构化、非结构化数据,数据处理需要快速,这对大数据的存储、挖掘和分析带来极大的挑战.Hadoop是分布式大数据处理平台,Spark是一个开源并行云计算平台,是一个流行的计算框架,拥有Hadoop MapReduce具备的优点[1].Matlab是一款可开发算法、进行数据分析及数据可视化的优秀软件,可用Matlab进行大数据分析与挖掘,南开大学博士马文辉把Hadoop/Spark与Matlab进行集成,实现大数据的处理与挖掘.
遥感大数据处理是典型的大数据应用方向之一[2].随着传感器技术的发展以及信息化的广泛应用,遥感图像已经成为信息产业的主要数据来源之一[3-6].高分辨率的遥感图像不仅能够直观反映地理资源的分布情况,而且可以为地理信息产品提供诸多信息[7-9].然而,由于遥感图像数据时空分辨率、光谱分辨率等不断提高,数据类型不断增加以及基于多平台的传感器组网系统的广泛应用,遥感数据具有典型的大数据特征.这给数据传输和数据存储都带来极大的压力[10-11].
图像压缩技术为解决上述问题提供了一种有效的策略[12-13].遥感图像经过灰度处理后,可以看作元素为灰度值的二维矩阵.因为遥感图像分辨率高,相邻像元间的相关性较强,所以与遥感图像对应的数据矩阵一般具有较大的冗余度[14].一般地,遥感图像的冗余可以通过矩阵的秩来衡量:秩较高的图像矩阵各列元素彼此的相关程度低,秩较低的图像矩阵各列元素彼此的相关程度高.因此,针对遥感图像进行数据压缩,不仅有利于节省通信信道的带宽,还能够提高数据的传输速率以及系统的可靠性.
在图像压缩技术中,矩阵分解是重要的理论组成部分.它通过将原始矩阵拆分成具有不同性质的矩阵的乘积,来描述矩阵隐藏的属性及彼此间的联系,从而实现各种高效的压缩算法.其中,奇异值分解(Singular Value Decomposition, SVD)是典型的矩阵分解方法[15].为此,本文采用SVD方法,针对遥感图像进行数据压缩,并采用实测遥感图像数据验证提出算法的性能.
1 SVD的基本理论

λi≥λi+1,且λn≥0
(1)

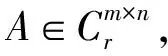
A=UΣVH
(2)
那么,酉矩阵U的每一列称为矩阵A的左奇异向量,酉矩阵V的每一列称为矩阵A的右奇异向量.其中,Σ是由矩阵A的r个奇异值构成的广义对角矩阵.
2 基于SVD的遥感图像压缩
经过灰度处理后,遥感图像可以看作元素为灰度值的二维矩阵.因为遥感图像数据分辨率高、数据量大,像素间的相关性较强,所以遥感图像对应的数据矩阵一般具有较大的冗余度[14].遥感图像的冗余度可以通过矩阵的秩来衡量.如果图像矩阵的秩越高,那么矩阵各列元素的相关程度越低.相反,如果图像矩阵的秩越低,那么矩阵各列元素的相关程度越高.考虑到SVD的优点,这里将SVD用于遥感图像压缩.
针对(2)式,将SVD改写为外积的形式:
A=UΣVH=(u1,u2,…,um)
(3)
经过非零奇异值的外积展开后,很容易发现其他外积项(乘积为零)实际上是冗余数据,对矩阵A没有任何贡献.为此,可以采用SVD处理遥感图像,剔除零奇异值对应的奇异向量,从而实现遥感图像的数据压缩.
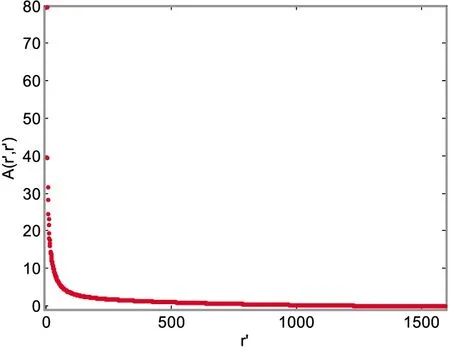
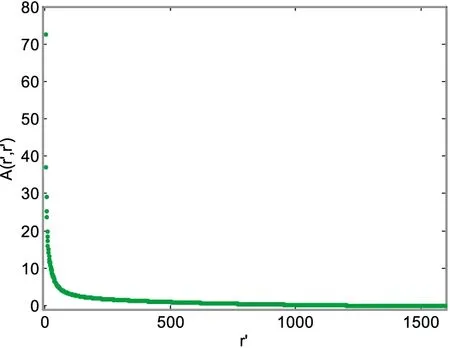
考虑到噪声对遥感图像的影响以及遥感图像内容的复杂性,在实际中图像矩阵可能是满秩的.即非零奇异值的个数等于矩阵的行数或列数.此时,简单地剔除多余的奇异向量并不能实现遥感图像的数据压缩.理论上,图像中相似度较强的区域一般是线性无关的,但是它们可以被近似看作线性相关的.尽管这将产生很小的奇异值,但是这种由像素间微小差异所导致的线性无关对于图像整体表征的影响可以忽略不计.因此,可以剔除SVD外积展开式中奇异值λk较小的外积项(0 (4) 奇异值压缩方法主要步骤如下: (1)获取原始遥感图像的矩阵A,并提取R、G、B三个通道的遥感图像数据AR、AG和AB. 此外,如果选取r′个奇异值以及这些奇异值对应的左、右奇异向量重构原始遥感图像,可以进一步定义图像的压缩比率为: (5) 实验采用的遥感图像为jpg格式的MODIS遥感图像数据.实验平台参数为:Intel(R)Core(TM)i3-9100 CPU @ 3.6 GHz,内存8.00 GB,运行环境Matlab r2009b.在实验中,首先调用Matlab自带函数读取图像数据,并提取R、G、B三个通道的图像数据AR、AG和AB,分别用3个1596*1974阶的图像矩阵,如图1所示. 图1 原始图像和分量图像 针对任一通道的分量图像,分别将分量图像读入Matlab中,存储为数据矩阵Ai,并将其转换为double型,以适应SVD函数的要求;然后运用函数[U,Σ,V]=svd(Ai)进行奇异值分解,可以分别得到1596*1974的对角奇异矩阵Σ,1596*1596的左奇异矩阵为U,1974*1974的右奇异矩阵为V. 提取遥感图像矩阵的奇异值作为行向量,可以分别得到对应三个通道分量图像的奇异值曲线,如图2-4所示.利用分解后的分量图像矩阵可以重构图像,即r′=10,40,80,100,200,400,800,1200,1596,如图5-7所示.此外,利用三通道的分量图像可以进一步合成RGB图像,如图8所示. 图2 R通道图像奇异值曲线 图3 G通道图像奇异值曲线 图4 B通道图像奇异值曲线 图5 R通道图像重构 图6 G通道图像重构 图7 B通道图像重构 图8 重构图像 从图2-4可以看出,奇异值衰减很快.从图5-7可以发现数值越大的奇异值对图像的贡献率越大,数值越小的奇异值对图像的贡献率越小.取前40个奇异值,就可以基本重构清晰的原始图像,且不会带来较大的失真.如果压缩数r′越小,那么需要保存的数据就越少,重构后的图像与原始图像相差越大.此时,重构后的遥感图像会非常模糊.相反,如果压缩数越大,那么需要保存的数据越多,重构后的图像与原图像相差越小.此时,重构后的图像会比较清晰.当压缩数r′等于原始图像的维数时,重构图像与原始遥感图像基本一致.此外,表1进一步给出不同压缩数r′下的压缩比例值. 表1 遥感图像的压缩比率值 本文首先分析遥感图像的特点和存在的问题,并提出一种基于奇异值分解(SVD)的遥感图像压缩方法.该算法主要通过SVD分解方法获取遥感图像的压缩矩阵,然后选取局部压缩矩阵重构原始遥感图像的近似图像.同时在分解过程中,通过压缩矩阵的奇异值曲线可以获取奇异值的衰减规律以及与奇异值对遥感图像的贡献程度.此外,通过选取不同的压缩值可以实现不同压缩效果.实验结果表明,基于奇异值分解的遥感图像压缩方法能够有效地实现遥感图像的压缩,具有良好的压缩效果.





3 实验结果与分析







4 结束语
