微观经济学中消费者最优决策的补偿变化与等价变化

杨卫涛，秦建辉

（1.开封大学 财政经济学院，河南 开封 475004；2.河南理工大学 党委组织部，河南 焦作 454003）

一、引言

西方经济学在有关消费者理论中创造出“效用”这一测量主观感受的方法，以此来研究消费者行为。效用是指消费者在消费过程中所获得的满足感，它是可以量化满足程度的一种测量方法，通过它可以看出满足程度的高低。这里所说的效用又分为基数效用和序数效用。基数效用侧重于微积分代数形式，而序数效用侧重于几何图形方法，二者搭配使用，能更好地反映出在市场经济环境下，消费者是如何决策的［1］P38－42。

效用这一方法是用来测量主观感受的，然而，用基数效用和序数效用测量出来的主观满足程度并不直观。现实中，利用货币（金钱）来测量消费者的主观满足程度比较直接也很方便。补偿变化和等价变化就是，利用货币去测量消费者在面对商品价格和收入等市场经济环境因素变化时自身的利益变化以及所做出的最优决策选择。关于消费者最优决策的分析方法，大致分为两类：几何图形方法和微积分代数形式。初级微观经济学主要利用无差异曲线＆预算约束线几何形式和拉格朗日最优化方法来静态分析；中级微观经济学在两类方法上进行了深化，比如：对几何图形进一步细化，将拉格朗日解法分为角点解和内解；高级微观经济学则运用动态分析方法和博弈论等理论来研究。

国内主流教材中对补偿变化和等价变化的讲解，要么偏重于数理推倒（一般来说，要求对微积分学得较为扎实，这样才容易理解），要么含糊其辞，一带而过。学生不理解，只能死记硬背，这造成了初学者的阅读障碍，学生不知道为什么学，学了有什么用，从中得不到学习的乐趣。比如，平新乔《微观经济学十八讲》中，大部分都是数学公式推导［2］P23－28；范里安《微观经济学：现代观点》中，虽数学公式推导不多，但没有充分利用几何图形工具［3］P120－135。本文针对目前补偿变化和等价变化教学中存在的这些问题，在已有研究成果的基础上，利用几何图形，提出“平行线三点法”，以此来计算和反映这两种变化。

二、问题的提出

从国内对微观经济学教材讲授阶段的划分来看，初级微观经济学部分没有涉及补偿变化和等价变化，中级微观经济学部分仅涉及两个商品的等价变化和补偿变化。本文以中级微观经济学中的两个商品为例，引出等价变化和补偿变化的测量问题。

消费者在市场上消费两种商品X和Y，其初始价格分别是PX和PY，初始预算收入为M，初始预算线为AB，初始的最优消费决策是无差异曲线U1与预算约束线AB的切点E0。此时，消费者在这个“静止”的市场环境下，沿着最优消费决策路径走，以使自己的效用最大化或利益最大化。市场环境是多变的。在我们设置的简单市场模型中，只有三个变化的量：商品X的价格、商品Y的价格和消费者的预算收入M。而且，三个变量的变化有正负两个方向，所以在静态分析中，共有6种变化情况。

现在我们只分析商品X的涨价情况①其他变化情况，同理可得。，分析涨价对消费者决策的影响。当商品X的价格上升时，其预算约束线AB变化为AC②为了配合分析等价变化和补偿变化，尽可能使图形简单，未考虑消费者的初始禀赋情况。，最优消费决策是预算线AC与无差异曲线U2的切点E1。如图1所示。

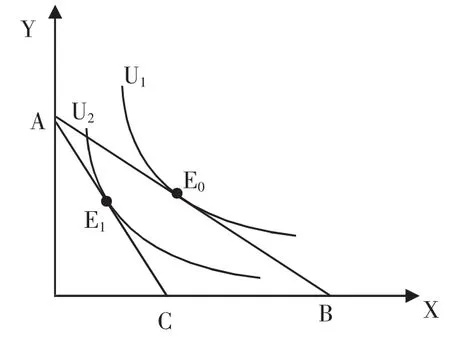
图1 消费者最优决策

可以看出，在商品X涨价前后，消费者的最优消费决策状态E0和E1是不一样的，它发生了变化。现在，只有商品X的价格上涨了。价格上涨，生活成本高了，消费者肯定会遭受损失。那么，我们能不能将商品X涨价后的价格差作为变化或损失呢？显然不能，因为消费者处在一个系统的市场环境中，商品与其价格之间，以及商品价格与收入之间互相“牵制”，它们处在一个互动的环境中。那么，究竟如何用货币来衡量这种变化或损失呢？

三、补偿变化

市场环境不断发生变化。商品X的价格上涨后，消费者的处境与之前相比，显然变得糟了。那么，我们应该给消费者多少货币补偿，才能使其处境与涨价前保持一样呢？再直白点说，就是：商品涨价，造成消费者的购买力下降了。那么，要补给消费者多少钱才能使其生活水平不受影响呢？给消费者的货币补偿就是其因商品涨价而遭受的损失，这样才能达到使其生活水平不受影响的目的。这就是“补偿变化”这一名词的来历。只不过当价格下降时，它是一种“负补偿”。

现在，我们根据补偿变化的定义和无差异曲线的含义，用图形来表示补偿变化。西方经济学常用无差异曲线来衡量消费者的处境［4］。若消费者的处境在涨价前和涨价后一样好，那么，涨价前后的消费者最优决策应该处在同一条无差异曲线上。而由预算约束线可知，其斜率代表的就是两个商品价格之比。预算约束线AB的斜率代表两个商品初始价格比，预算约束线AC的斜率则代表商品X涨价后两个商品的价格比。

图2反映了补偿变化。“消费者在商品X涨价后的处境和涨价前一样好”，图2中的那条虚线表示这种情况。这条虚线有两个特征：第一，它和AC平行，表示商品X涨价后两个商品的价格比，说明消费者面临涨价后新的市场环境；第二，它和初始无差异曲线U1相切于点E2，表示在新的市场环境中，消费者的处境保持不变。

图2中有两条平行线：虚线和AC；还有三个点：E0、E1和E2。此即为“平行线三点法”。AB为初始市场环境下消费者的预算约束线，AC为市场环境发生变化后消费者的预算约束线；E0表示初始市场环境中消费者的最优决策点，E1表示市场环境变化后消费者的最优决策点，E2表示市场环境变化后消费者的处境与初始市场环境中的处境一样时的最优决策点。

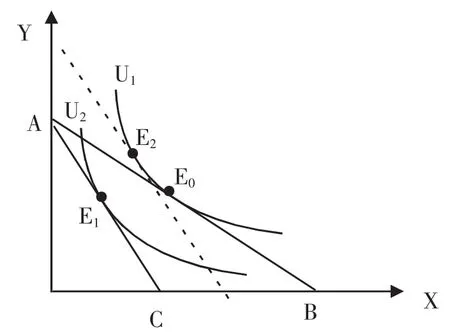
图2 补偿变化

用货币测量补偿变化，就是计算E2点的消费者收入与初始收入之间的差额。结合几何图示，配合使用消费者最优决策代数方法，能够很容易地计算出补偿变化。

四、等价变化

等价变化是用货币测量消费者面临市场环境变化而受到的影响程度的另一种方法［5］。沿用前边分析的市场环境变化情况，当商品价格上涨时，消费者的处境发生了变化。要想保持消费者处境不变，就需要给其补偿一定的货币。现在换一个思路：假如商品X不涨价，那么需要从消费者那里取走多少货币，才能使其涨价前后的处境一样呢？这种变化叫做等价变化。之所以叫“等价”，是因为如果消费者的处境变坏，那么使商品价格上涨与从其手中取走货币，效果是等价的。等价变化就是用货币去测量这种变化。

我们依然用预算约束线和无差异曲线来分析等价变化。让商品X涨价和从消费者手中取走货币，对消费者处境的损害程度一样。就是说，两种情况下，消费者的处境一样。因此，在这两种情况下，消费者的最优决策点在同一条无差异曲线上。

图3反映了等价变化。“让商品X涨价和从消费者手中取走一定数量的货币，消费者在这两种情况下的处境一样好”，图3中的那条虚线表示这种情况。这条虚线有两个特征：第一，它和AB平行，表示在商品X没有涨价情况下两个商品的价格比，说明消费者面临商品没有涨价但收入被取走一部分的新的市场环境；第二，它和初始无差异曲线U2相切于点E2，表示在商品价格不变但收入被取走一部分后消费者的处境和商品涨价情况下的处境一样（等价）。

图3中也有两条平行线：虚线和AB；还有三个点：E0、E1和E2。此即为“平行线三点法”。AB为初始市场环境下消费者的预算约束线，AC为市场环境发生变化后消费者的预算约束线；E0表示初始市场环境中消费者的最优决策点，E1表示商品X涨价后消费者的最优决策点；E2表示商品X不涨价而从消费者手中取走一部分货币后消费者的最优决策点。

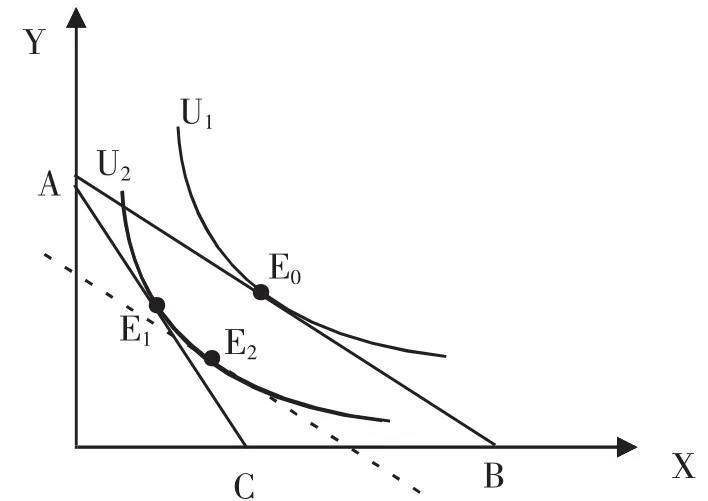
图3 等价变化

用货币测量等价变化，就是计算E2点时消费者的收入与初始收入之间的差额。结合几何图示，配合使用消费者最优决策代数方法，能够很容易地计算出等价变化。

五、实例分析

某消费者的效用函数为U（X，Y）＝X0.5Y0.5，在初始市场环境下，两个商品的价格PX和PY分别是（1，1），收入M为100。那么，当商品X的价格上升到2时，补偿变化和等价变化各是多少？此案例被众多中级微观经济学教材收录，解法雷同。下面，利用“平行线三点法”来分析该案例。

第一步：套用公式，列出最优决策的代数表达式。

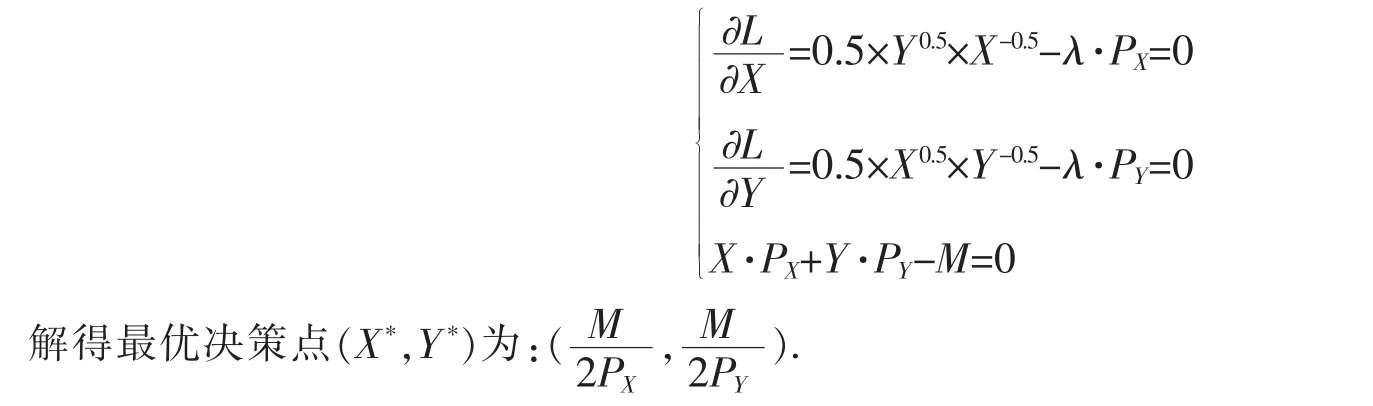
第二步：依照图2来分析，计算补偿变化，直接瞄准两个最优决策点。

E0表示初始市场环境中消费者的最优决策点。此时，M＝100，PX＝1，PY＝1.代入最优决策点（X*，Y*）公式，得到最优决策点为（50，50），此时的效用为 50。

E2表示市场环境变化后消费者的处境和初始市场环境下的处境一样的最优决策点。此时，M未知，PX＝2，PY＝1，代入最优决策点（X*，Y*）公式，得到最优决策点为。

因为E0和E2两点的效用一样，所以

计算E2点时消费者的未知收入，得到

比较E0和E2两点，消费者收入的差额就是补偿变化：

第三步：依照图3来分析，计算等价变化。

E1表示商品 X 涨价后消费者的最优决策点。此时，M＝100，PX＝2，PY＝1.代入最优决策点（X*，Y*）公式，得到最优决策点为（25，50），此时的效用为。

E2表示商品X不涨价而从消费者手中取走一部分货币后消费者的最优决策点。此时，M未知，PX＝1，PY＝1.代入最优决策点（X*，Y*）公式，得到最优决策点为。

因为E1和E2两点的效用一样，所以

计算E2点时消费者的未知收入，得到

比较E1和E2两点，消费者收入的差额就是等价变化：

六、总结

补偿变化和等价变化衡量的是市场环境发生变化时消费者处境的变化程度，处境是指消费者购买商品后的主观感受，它用货币去测量［6］。从几何图形上可以更加直观地看到，计算补偿变化和等价变化就是测量两条无差异曲线间的距离。我们根据情况，添加了平行线，用计算两条平行线之间距离的方法，来近似计算两条无差异曲线之间的距离。在计算中，只需要列出最优解的一般表达式，然后结合两个最优点的状态，代入各个变量的具体数值，就可以计算出补偿变化和等价变化。分析问题时，我们用到了两条平行线和三个均衡点。计算时，只用两个均衡点就得到了结果。

补偿变化和等价变化是中级微观经济学的两个重要知识点，是理解和研究消费者决策行为的重要工具［7］。帮助学生理解和掌握它们，对提高学生分析经济问题的能力以及他们的后续学习都有很大帮助。

（注：本研究得到开封大学区域经济研究所资助）