大规模图顶点覆盖的增量算法研究

乔 龙，陈德刚

(华北电力大学 数理学院，北京 102206)

0 引言

顶点覆盖问题[1]在图论中是一个著名的NP完全问题，在现实生活中应用非常广泛。例如，博物馆展览柜设计、大型网络监控节点的布置、大型交通运输线路网络设计、集成电路设计等等。在人工智能大数据时代背景下，在实际问题中涉及的往往是动态图，针对于这种具有增量变化的动态图设计出一种智能化的求解顶点覆盖算法无疑具有重要的应用价值。

近年来，国内外学者设计出了一系列求解极小顶点覆盖集合的算法，但就其增量问题的相关研究却很少。求解图的极小顶点覆盖集合，其传统的思想是利用布尔变量的运算[1-2]，这是最基本的求解方法。但是其运算复杂度，尤其是面对大规模的图结构模型问题时，达不到高效性的要求。吴春等[3]基于顶点覆盖问题的理论研究，发现最小点覆盖问题、最大独立集问题与最大团问题三者事实上是等价的。对于网络监测点部署，陶星宇[4]针对原有网络中布置的监测点不易变动的问题，提出了一种增量网络监测点的增量选取算法。丁三军等[5]和Zhou T等[6]基于贪婪算法的思想研究了极小顶点覆盖的求解与更新问题。占善华等[7]提出了一种更新最小顶点覆盖的增量式属性约简算法。苗董晶等[8]研究了冲突图中的极小顶点覆盖算法。Wang L等[9]设计出的分支定界算法解决了大量图的极小权重覆盖问题。对于加权顶点覆盖，Fukunaga T等[10]求解出了加权的无向图的最小权重的Steiner树。Tang C等[11]利用博弈论的思想把加权顶点覆盖问题建模为不对称的博弈。寇磊等[12]基于Dijkstra 算法,以最短路长的最大值为标准,按照一定原则筛选出点覆盖集合的顶点。王丽丽等[13]利用线性规划松弛的方法实现对计算复杂度进行预测，在求一个图论模型的点覆盖集合上取得了不错的效果。聂晓燕等[14]和高琳等[15]研究了DNA计算标签的最小顶点覆盖问题。郑少萍[16]和袁启杰等[17]研究了Petersen图的极小顶点覆盖集合的求解问题。这些研究进一步丰富了极小顶点覆盖的理论。

在上述研究中，这些算法所面对的大部分是静态图。在面对动态图的时候没有包含快速的更新顶点覆盖的理论机制，因而在图的规模扩张时需要重新计算顶点覆盖，会占用大量的计算和存储资源。本文旨在针对大规模图的增量变化问题，找到可以高效更新顶点覆盖的增量算法。为了研究出一种智能化更新极小顶点覆盖的算法，并且就其时间复杂度而言满足其高效性，我们从图的极小顶点覆盖集合的定义出发，对大规模图顶点数目增加、边数目增加和顶点与边数目均增加3种动态过程分析了顶点覆盖的增量机理。在此基础上通过对图的存储矩阵、邻接矩阵和关联矩阵进行更新，设计顶点覆盖的更新迭代算法，使得更新后的极小顶点覆盖集合能够覆盖到更新后图中的所有的边，并且能够剔除图中的冗余顶点，能够较快地得出较优的解。

1 图的预备知识

图G由一个有序的二元组G=组成，其中V为图G的点集，E为图G的边集。对于∀v∈V，e∈E，用V(v)表示顶点v所邻接的顶点，用V(e)表示边e连接的一组顶点。对于图G中的边集E={ei|ei∈E,i=1,2,…}中的ei一般可以分为有向边和无向边。基于此特征把图分为两类：其边没有方向的图称为无向图，否则称为有向图。本文仅考虑无向图的增量问题。对于一个传统的图，它的边集满足E⊆V×V，否则该图就被定义为超图。对于图中的2个顶点vp、vq，如果存在一条边同时与vp、vq相连，那么称顶点vp、vq是相邻接的，若2条边ep、eq同时关联于同一个顶点，称此2条边ep、eq是相邻的。没有边关联的顶点被称为孤立点。若一条边关联的2个顶点是相同的，那称此边为环。

为了把一个图结构存储于计算机中，其所具有的特性一般会通过图的邻接矩阵和关联矩阵的形式来进行计算机操作与处理。这两种表示方法在表示相同图时具有唯一性，并且同一个图的邻接矩阵与关联矩阵之间可以进行转化。

设G=是简单无向图，S为一个集合，S⊆V且S≠φ，若E中的每条边都和S中的某个顶点相关联，则S是G的顶点覆盖集。对于上述的点覆盖集合S，若对∀vi∈S⊆V，有S-{vi}都不是点覆盖集合，那么S就是G的极小顶点覆盖集合。

对于求解顶点覆盖问题需要引出独立集这个概念：集合I是V的非空子集，若I中任意两个顶点都不相邻，则I是图G的独立集。

2 极小顶点覆盖问题的增量算法

2.1 顶点覆盖的增量问题

当给定图的顶点或者边数目发生增量变化时，原图的极小顶点覆盖集合是新图点覆盖集合的一个局部最优解，因而需要将这个局部最优解扩展成为全图的一个全局最优解。考虑到以下两种情况：1)顶点的增加：当新增加的顶点只与原顶点覆盖集合中的顶点相连时，则更新后的顶点覆盖集合保持不变；当新增加的顶点只与非原点覆盖集合中的顶点相连时，那么此时顶点覆盖集合也要随之发生变化，此时便需要在原点覆盖集合的基础上增加或者删除若干个顶点；当新增加的顶点既与原点覆盖集合中的元素又与非原点覆盖集合中的元素相连，那么可以不考虑新增加的点与原点覆盖集中的点相连的边。2)边的增加：当边新加到原始图中时，可以分为两种情况，其一是该边与原点覆盖集合中的点相连，这种情况易知新图的点覆盖集合保持不变；其二是该边只与非原点覆盖集合中的点相连，这种情况下，则更新后的点覆盖集合便需要考虑增加必要的顶点和删除冗余的顶点，冗余的顶点即为不必要的顶点。

定理1设图G=，顶点集为V={v1,v2,…,vi}，边集为E，极小顶点覆盖集合为N0，新加入顶点vi+1，若对∀em∈E(vi+1)，都存在vm∈N0，使得em与vm相关联，则N0不发生变化。

证明由题意可知，加入顶点vi+1，对∀em∈E(vi+1)，都存在vm∈N0，使得em与vm相关联，那么则有：当m=1时，e1与顶点vi+1相关联，即为新加入的边，因为存在v1∈N0，使得e1与v1相关联。根据顶点覆盖的定义可知，边e1已经被顶点v1所覆盖，而v1是N0中的顶点，那么可得N0已经覆盖了与vi+1关联的一条边e1。同理当m=2时，可证N0已经覆盖了与vi+1关联的一条边e2。假设当m=1，2，…，m时，N0已经覆盖了与vi+1关联的一条边em，下证当m=m+1时成立。当m=m+1时，em+1和顶点vi+1相关联，em+1仍为新加入的边，因为存在vm+1∈N0，使得em+1与顶点vm+1相关联，且vm+1∈N0，那么可得N0已经覆盖了与vi+1关联的边em+1。综上所述，加入顶点vi+1而导致增加的边em此时均被原极小顶点覆盖集合N0所覆盖，所以更新后的图结构模型极小顶点覆盖集合不发生变化。定理得证。

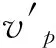
例1如图1所示，已知图G=，且它的其中一个极小顶点覆盖集合为N0={v1,v4,v5}，如果新加入顶点为vi+1，利用上述定理求解更新后的极小顶点覆盖集合Nnew。

由图可以看出，新加入的顶点vi+1与非顶点覆盖集合N0中的元素v2、v5相邻接，求解步骤如下：

第一步先在原点覆盖集合N0中分别加入顶点v2、v5；

第二步分别判断与v2、v5相连的原N0中的顶点中是否存在冗余的顶点。对于和v2相邻接的顶点有v1、v3，在比较过程中优先删去N0中度数较少的顶点。对于v1，与v1相连的所有的顶点是v2、v3，它们都属于N0中的顶点，根据定理2，此时v1可以删去。对于v3，与v3相连的所有的顶点为v1、v2、v4、v5，它们都属于N0中的顶点，而删去v1后，v3便不能再被删去。对于v4，与v4相连的所有的顶点为v3、v5，它们都属于N0中的顶点，因此根据定理2可以删去顶点v4。则有Nnew1=N0+{v2}-{v1}+{v5}-{v4}={v2,v3,v5}；

第三步求得顶点覆盖集合Nnew2=N0+{vi+1}={v1,v3,v4,vi+1}；

第四步计算并比较Nnew1与Nnew2集合中元素的个数，选取元素个数较少的集合为更新后的Nnew，更新后的极小顶点覆盖集合为：Nnew=Nnew1={v2,v3,v5}。

定理3设图G=，顶点集是V，边集为E={e1,e2,…,ei}，极小顶点覆盖集合是N0，新加入边为ei+m，若对∀ei+m都有∃vm∈N0，使得ei+m与vm相关联，则原极小顶点覆盖集合N0不变化。

证明由题意知，当加入边ei+m时，都有∃vm∈N0，使得ei+m与vm是相关联的，那么则有：当m=1时，ei+1作为新加入的边与v1相关联，而v1∈N0，根据顶点覆盖的定义可知，边ei+1已经被顶点v1所覆盖，而v1是N0中的顶点，那么可得N0已经覆盖了边ei+1。同理当m=2时，可证N0已经覆盖了边ei+2。假设当m=1,2,…,m时，N0已经覆盖了边ei+m，下证当m=m+1时成立。当m=m+1时，边ei+m+1仍为新加入的边，已经被顶点vm+1所覆盖，且vm+1∈N0，因此原顶点覆盖集合N0已经覆盖了图G中新加入的边ei+m+1。综上所述，新加入的边ei+m均已被原顶点覆盖集合N0所覆盖，即更新后的图结构模型的极小顶点覆盖集合N0不发生变化。定理得证。

定理4设图G=，顶点集是V，边集为E={e1,e2,…,ei}，极小顶点覆盖集合是N0，新加入边为ei+1，若∃vp,vq∈V-N0，使得ei+1与vp、vq同时相关联，令V(ei+1)={vp,vq}，则有如下结论：

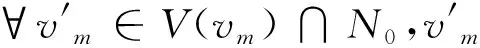
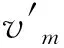
例2如图2所示，G=，而且利用属性约简的方法求出它的其中一个点覆盖集合为N0={v1,v4,v5}，新加入边ei+1，与顶点v3、v6相关联，利用定理4求解更新后的顶点覆盖集合Nnew。

由图可以看出，新增加的点ei+1与顶点v3、v6建立了新的邻接关系，求解步骤如下：

第一步依据定理4，把v3或者v6分别添加到点覆盖集合N0中，然后分别考察与v3和v6相连的顶点；

第二步如果考虑把v3加入到点覆盖集合中，那么与v3相连的顶点是v1、v4。对于v1，与v1关联的所有顶点为v2、v3，其中v2是非N0中的元素，根据定理4，v1不能删去。对于v4，与v4关联的所有的顶点为v1、v2、v5、v6，其中v2、v6为非N0中的元素，因此v4不能删去，可得Nnew1=N0+{v3}={v1,v3,v4,v5}；

第三步如果考虑把v6加入到点覆盖集合中，那么与v3相连的顶点是v4、v5。对于v4，具上所述v4是不能删去的。对于v5，与v5关联的所有的顶点为v4、v6，均是原N0中的元素，因此v5可以删去，可得Nnew2=N0+{v6}-{v5}={v1,v4,v6}；

第四步比较Nnew1与Nnew2集合中元素的个数，选取元素个数较少的集合为更新后的Nnew，更新后的顶点覆盖集合为：Nnew=Nnew2=N0+{v6}-{v5}={v1,v4,v6}。

2.2 求解增量式顶点覆盖的算法

在这一部分，我们设计了一种新型的求解增量式顶点覆盖的算法。给定一个图G=，它的邻接矩阵A(G)是一个|V|×|V|的实对称矩阵，由邻接矩阵相应的能求出图的关联矩阵。它的极小顶点覆盖集合是N0，从关联矩阵中可以发现N0中的所有顶点已经覆盖了E中的所有元素。当图结构发生增量变化时，它的极小顶点覆盖集合变化情况分为以下3种情况：原顶点覆盖集合不发生变化；原顶点覆盖集合加入若干个必要的顶点；原顶点覆盖集合添加若干个必要的顶点同时删除属于原顶点覆盖集合中冗余的顶点。

算法1求解顶点增量变化极小顶点覆盖集合

输入：图G=，极小顶点覆盖集合为N0，其邻接矩阵为A(G)；

输出：新的图结构的极小顶点覆盖集合Nnew。

对于j=1,2,…,m，新加顶点vi+j，令Vj={vi+j|j=1,2,…,m}；

步骤1判断vi+j是否与N0中的顶点邻接。如果与N0中的顶点邻接或者没有顶点与vi+j相邻接，则Nnew1=N0。否则转步骤2；

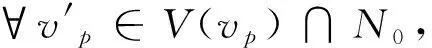
步骤3取Nnew=min{Nnew1,Nnew2,Nnew3,Nnew4|点覆盖数最小}。

算法2求解边的增量变化极小顶点覆盖集合

输入：图G=，极小顶点覆盖集合为N0，其邻接矩阵为A(G)；

输出：新的图结构的极小顶点覆盖集合Nnew。

对于j=1,2,…,n，新加边为ei+j；令Ej={ei+j|j=1,2,…,n}；

步骤1判断ei+j是否与N0中的顶点关联。若∃vm∈N0，使得ei+1与vm是相关联的，则Nnew1=N0；

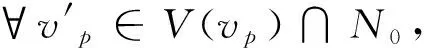
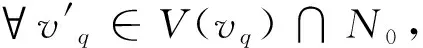
步骤4取Nnew=min{Nnew1,Nnew2,Nnew3|点覆盖数最小}。

上述两个算法分别展示了与顶点的增量变化和边的增量变化相对应的算法。当图发生增量变化时，要明确区分是顶点的还是边的增量变化或者两者均有，以便调用相对应的算法。算法1适用于图结构模型中顶点发生增量变化时的情况，算法2适用于图结构模型中边发生增量变化时的情况。当同时发生顶点和边的增量变化时，把两种情况拆分开来，先考虑顶点的增量变化，调用算法1，再考虑边的增量变化，调用算法2。本文算法1的时间复杂度为o(|Vj|)，算法2的时间复杂度为o(|Ej|)，算法的运行时间的变化取决于新加入顶点与边的数目，且随顶点与边的数目的增长呈线性增长。

3 实验对比

算法的仿真分析过程在Windows 10系统下进行。计算机硬件配置是Radeon R52.40 GHz，4GRAM，用到的计算机处理程序是Matlab 2018a与python3.0。数据来源为计算机编码生成的随机无向图。实验比对结果如表1、表2所示。

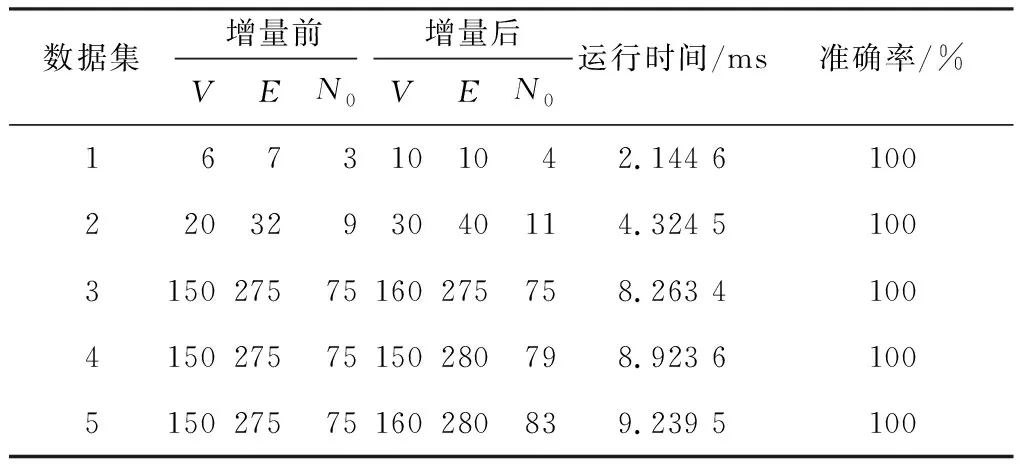
表1 图的增量实验比对

表2 算法时间复杂度实验比对

表1中数据类型分为增量前的极小顶点覆盖数和增量后的极小顶点覆盖数，算法运行时间是在对各个数据运行10次后取的平均运行时间。利用python运行算法时，第一次运行会出现运行时间较长，故第一次运行时间不取值，之后的运行时间两者差值基本上在0.5 ms内。这里的准确率代表算法运行后所得到的极小顶点覆盖集合是否有意义，如果所得到的极小顶点覆盖集合能满足其定义，可以覆盖更新后图结构中的所有的边，那么所得到的极小顶点覆盖集合是准确的。

另外我们通过实验数据检验该算法相比非增量的算法是否更具有高效性，实验结果如表2所示。对其算法的时间复杂度分析发现，文献[3]算法运行时间在顶点数较少时会出现运行时间为0的情况，但是随着顶点数目的增加，算法运行时间是明显增加的，而本文算法运行时间增加的速度更慢，因此本文算法相比文献[3]算法更具有高效性。

算法首次模拟是对文章中例子的模拟，然后对顶点数和边数进行递增实验，在表1中第3、4、5条数据集中采用了控制变量的方法，分别对只增加顶点、只增加边、顶点和边同时增加的情况进行了研究。得到：只增加顶点而边集不发生变化对极小顶点覆盖集合没有影响，只增加边直接调用算法2进行求解，顶点和边同时增加需要调用算法1和算法2。本节的实验验证了本文算法的准确性是较高的，算法求出的极小顶点覆盖集合能够满足大规模图发生增量变化时快速求解极小顶点覆盖集合的需求。

4 结束语

本文针对于极小顶点覆盖问题的增量情况，从极小顶点覆盖集合的定义出发，设计了求解顶点增量变化极小顶点覆盖集合的算法以及求解边的增量变化极小顶点覆盖集合的算法。有效地解决了对于图结构发生增量变化的极小顶点覆盖集合的更新问题。随着大数据时代的到来，数据的存储量将是大规模的，该算法对于大型网络监控节点的动态布置与重新确定图结构来求解出点覆盖集合相比更具有高效性。