基于聚类的变邻域模拟退火算法求解VRPTW

蔚 帅，蒋洪伟

(北京信息科技大学 信息管理学院，北京 100192)

0 引言

车辆路径问题(vehicle routing problem,VRP)是一个NP难题。VRPTW(vehicle routing problem with time window)是在VRP的基础上增加了时间窗约束条件，主要优化目标为最小化车辆数目、最小化总行驶距离、最小化总成本等。国内外大量学者对此提出了解决方案。Sim等[1]提出了生成性和选择性相结合的超启发算法，相比同类的超启发算法具有较优的求解效果；Crainic[2]提出了VRP的精确解和元启发式解并行求解的方法，可以有效地解决车辆路径问题等大型复杂组合优化方案；Baldacci等[3]对多类型车辆路径问题提出了基于改进启发式算法的解决方案；Bartolini等[4]提出了一个求解VRP的精确解框架，该框架可以被建模为具有附加约束的集合划分问题；葛斌等[5]针对传统蚁群遗传混合算法中参数静态设置、冗余迭代及收敛速度慢等缺点，提出了动态混合蚁群优化算法；苏红畏等[6]采用了两个最大最小蚁群系统分别对配送车辆和行驶距离进行优化；李小川等[7]提出了基于文化基因的狼群算法，求解效果更好；殷亚等[8]提出了多种改进蝙蝠算法，并通过仿真实验验证了各个算法的寻优能力；段砚等[9]提出改进的人工蜂群算法，通过实例验证了算法可以有效地降低物流成本。在车辆路径问题的研究过程中，工作重心大都集中在算法的结合与优化，而忽视了对数据处理的研究。同时，对算法陷入局部最优解而导致解质量不高的问题优化不够。针对这些问题，本文提出了DBSCAN/SAVN来求解VRPTW。

1 问题描述及数学模型

1.1 问题描述

VRPTW可描述为已知一批顾客的位置坐标、货物需求量和待收货物的时间等信息，由k辆规格相同的车为n个顾客配送货物，在满足载重约束和时间窗约束的条件下，每辆车从配送中心出发，完成配送任务后返回配送中心。通过合理规划车辆的配送任务及运输路径，使配送车辆数和总距离的综合成本达到最小。

1.2 参数定义

为了能够清楚地描述VRPTW的数学模型，对模型中所用到的参数做如下定义：

N={1,2,...,n}：所有顾客点的集合；

K={1,2,...,k}：所有配送车辆的集合；

dij：顾客i与顾客j之间的距离；

Wk：车辆j的最大载重量；

ri：顾客i的货物需求量；

Pk：车辆k服务的顾客点集合；

[Tei,Tli]：顾客i的时间窗约束；

Tai：车辆到达顾客点i处的时间点；

Twi：车辆在顾客点i处的等待时间；

Tsi：顾客i处的服务时间。

1.3 数学模型

根据VRPTW的问题描述与参数定义，得到如下数学模型：

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

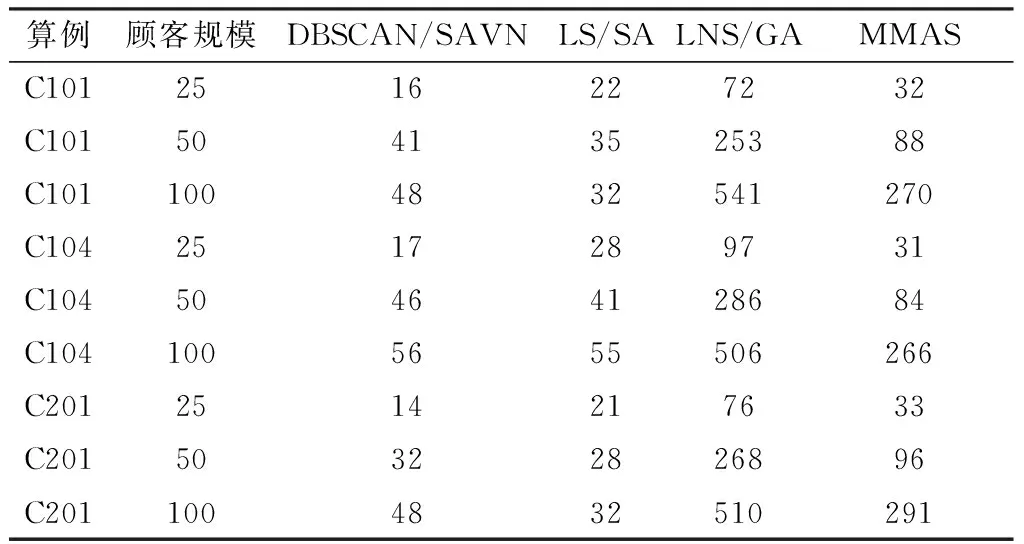
Tei

(11)

Twi=max{0,Tei-Tai}i∈N

(12)

式(1)和式(2)为决策变量；式(3)为最少车辆使用数的目标函数；式(4)为最小配送距离的目标函数；式(5)表示每辆车每次只能服务一个顾客；式(6)表示车辆的货物载重不能超过最大载重量；式(7)表示每个顾客只能被一辆车服务；式(8)表示每辆车的起点和终点都是配送中心；式(9)表示车辆k配送过程的连续性；式(10)表示每辆车只能形成一条配送路径；式(11)表示车辆只能在顾客要求的服务时间窗内完成配送服务；式(12)为车辆的等待服务时间。

2 DBSCAN/SAVN算法设计

2.1 DBSCAN聚类算法

在求解VRPTW中，聚类可以有效地缩小数据规模，可以提高后续启发式算法的求解速度与解的质量。聚类方法包括划分聚类、层次聚类、密度聚类、网格聚类和基于模型的聚类等。其中，基于密度的聚类方法(density-based spatial clustering of application with noise，DBSCAN)不需要提前确定簇类的个数，且聚类的方式能够克服基于距离的算法只能发现“类圆形”簇类的缺点，可以得到任意形状的区域簇类。因此使用DBSCAN对VRPTW中的顾客点进行区域划分，DBCSAN求解结果的正确性可以通过已知的Solomon标准测试集中的最优解来进行验证。

DBSCAN聚类求解步骤如下：

①扫描已知的顾客点坐标数据集，随机寻找一个核心点，然后找到从该核心点出发的所有密度相连的数据点，对该核心点进行扩充；

②遍历该核心点的ε邻域内的所有核心点，寻找与这些数据点密度相连的点，直到没有可以扩充的数据点为止；

③重新扫描顾客坐标数据集，寻找没有被聚类到的核心点并扩充，再重复步骤①和步骤②。没有包含在任何簇中的数据点就构成噪音点；

④对噪音点进行二次聚类，通过计算簇与簇中心间的距离，将剩余的噪音点归入离它最近的簇中。

2.2 变邻域模拟退火算法

模拟退火算法(simulated annealing，SA)是由Metropolis等提出的一种模拟物理中固体的物理退火过程的算法。作为一种经典的元启发式算法，具有计算过程简单、鲁棒性强的优点，用来求解多目标组合优化的问题。SA中的Metropolis准则能够在一定程度上克服算法陷入局部最优解的问题，让算法可以在一定概率下接受坏解，扩大局部搜索的范围。

变邻域搜索算法(variable neighborhood search,VNS)是一种改进型的局部搜索算法，利用不同的扰动算子构成不同的邻域结构，再对邻域结构进行交替搜索，直到VNS达到算法终止条件，当前状态下的最优解即全局最优解，邻域结构集合可表示为Ns={s′|对当前解s应用扰动算子生成s′}。变邻域模拟退火算法(simulated annealing with variable neighborhood，SAVN)即引入变邻域搜索算法的思想，结合Metropolis准则的双向随机搜索策略，保证SAVN在不同的邻域结构中找到高质量解，提高SA跳出局部最优解的能力，通过SAVN每次的迭代来降低温度，直到满足SAVN的终止准则。

2.3 SAVN的邻域结构设计

不同的扰动算子决定了不同的邻域结构，SAVN选择exchange算子、insertion算子和2-opt算子3种扰动算子来构造邻域结构，在迭代的过程中依次选择一种算子来扰动解的空间。

本文采用自然数编码的方式来解释3种扰动算子如何在VRPTW中构造不同的解。例如路径矩阵(0,r11,r12,…,r1n;0,r21,r22,…,r2n;0,rm1,rm2,…,rmn,0)，其中，0代表配送中心，第m行代表第m辆车服务的顾客点为rm1,rm2,…,rmn。假设现有2辆车为7个顾客点提供配送服务，则编码为0123405670时，代表第1辆车的配送路线为0-1-2-3-4-0，第2辆车的配送路线为0-5-6-7-0。

第1种扰动算子为exchange算子，类似于3-opt算子，但与其不同的是，exchange算子将两点交换。以编码0123405670为例，通过交换位置1的元素2与位置2的元素6得到候选编码0163405270如图1所示，通过exchange扰动算子得到的所有候选编码组成了SAVN的第1个邻域结构。

第2种扰动算子为insertion算子，是or-opt算子的一种特殊情况，即只对1个元素进行插入操作，而不是若干元素组成的片段在路径中重新插入。仍以编码0123405670为例，选择两个位置得到元素3和元素5，将元素5插入到元素3的位置后，得到候选编码0123540670如图2所示。通过insertion扰动算子得到的所有候选编码组成了SAVN的第2个邻域结构。

第3种扰动算子为2-opt算子，将两个位置之间的元素顺序进行翻转。仍以编码0123405670为例，选择两个位置得到元素1和元素4，将两个元素以及之间的元素交换位置，得到候选编码0432105670，如图3所示，通过2-opt扰动算子得到的所有候选编码组成了SAVN的第3个邻域结构。

2.4 DBSCAN/SAVN算法流程

本文采用DBSCAN/SAVN求解VRPTW的具体算法流程如图4所示。整个算法流程包括3个部分：第一部分是选择由DBSCAN算法产生的簇，对每个簇中的数据进行初始化参数设置；第二部分是在Metropolis准则和邻域结构的共同作用下，通过不断地迭代来寻找各个簇的高质量解；第三部分是将所有簇类迭代产生的解进行整合，形成VRPTW的完整解。

3 实验与结果分析

3.1 仿真环境设置

为了验证本文所提DBSCAN/SAVN求解VRPTW的效能，利用Matlab R2019b软件完成仿真实验，仿真环境为处理器Intel(R)Core(TM)i7-8700 CPU 4.3GHz，RAM 32GB，Win10操作系统的PC机。

3.2 算例及对比算法选择

本文采用Solomon标准测试数据集中的算例进行算法测试。为了验证DBSCAN/SAVN在不同顾客规模中的求解效果，采用3个顾客规模为25的算例，分别由C101、C104、C201的前25条数据产生；3个顾客规模为50的算例，分别由C101、C104、C201的前50条数据产生；3个顾客规模为100的算例，分别由C101、C104、C201的前100条数据产生。

为验证BDSCAN/SAVN的求解性能优于别的启发式算法，将DBSCAN/SAVN与基于局部搜索策略的模拟退火算法(simulated annealing with local search，LS/SA)[11]、基于大规模邻域局部搜索策略的遗传算法(genetic algorithm with large neighborhood search，LNS/GA)[12]，最大最小蚁群算法(max-min ant colony algorithm，MMAS)[13]进行比较。

3.3 算法参数设置

为了确保4种算法的求解结果具有可比性，对各算法的参数设置如下：

DBSCAN/SAVN算法参数设置中外层最大迭代次数Iomax为3000次，里层最大迭代次数Iimax为 300次，初始温度T0为5000，冷却因子α为0.99。

LS/SA算法参数设置与DBSCAN/SAVN相同，其中选择交换算子的概率Pe为0.2，选择2-opt算子的概率P2o为0.5，选择插入算子的概率Pi为0.3。

LNS/GA算法参数设置中最大迭代次数Imax为100，违反容量约束的惩罚函数系数α为10，违反时间窗约束的惩罚函数系数β为100，种群大小N为100，交叉概率Pc为0.9，变异概率Pm为0.1。

MMAS算法参数设置中蚂蚁数量m为20，信息素重要程度因子α为3，启发函数重要程度因子β为4，等待时间重要程度因子γ为3，随机选择概率阈值r为0.5，信息素挥发因子ρ为0.85；信息素浓度常数Q为5，信息素初始浓度τ0为0.1。

3.4 算法有效性检验

用DBSCAN/SAVN、LS/SA、LNS/GA和MMAS四种算法分别对9个算例进行求解，各算法对每个算例独立运行20次得出实验结果，保留20次实验结果中的最优解，结果如表1、表2所示。其中表1为4种算法求解结果的最优值，表2为4种算法的CPU运行时间。

从表1可以看出，DBSCAN/SAVN在不同顾客规模的算例中均得到了较优的解，尤其在顾客规模较大的情况下，求解的车辆数和总距离上均优于其他3种算法。其中，在顾客规模为100的C201算例中，DBSCAN/SAVN、LNS/GA和MMAS均取得了最优解，是由于该算例的顾客点分布较为密集，完成配送任务的车辆使用数少，容易获得高质量解。而LS/SA解质量的好坏依赖于初始解的优劣，且在顾客规模较大的情况下得到优解的概率小，在独立运行的20次实验中均未得到最优解。

表1 四种算法求解结果的最优值

从表2可以看出，DBSCAN/SAVN运行所花费的时间远远少于LNS/GA和MMAS。虽然LS/SA得到高质量解的概率小，但是LS/SA的算法结构较为简单，在求解各算例时花费的时间较少，尤其在顾客规模为100的情况下，LS/SA的CPU运行时间少于DBSCAN/SAVN。这是由于DBSCAN/SAVN在求解问题时，在DBSCAN算法将所有顾客划分为若干个簇类的基础上，又分别对每个簇类执行SAVN算法，加大了程序的整体执行次数，导致算法耗费的时间较多。

表2 四种算法的CPU运行时间 s

为了进一步验证DBSCAN/SAVN的性能，选择LS/SA作为对比算法，选取顾客规模为100的C101算例进行仿真实验。

首先，运用DBSCAN聚类算法对C101中的100个顾客划分簇类，由于C101的顾客点分布集中，每个簇类中顾客的数量较为均匀，在聚类的过程中没有产生噪音点，因此不需要二次聚类，DBSCAN/SAVN求解C101的聚类效果如图5所示。

然后运用SAVN算法分别对每个簇类进行计算，最后将所有簇类的计算结果进行整合，获得DBSCAN/SAVN求解C101的最优解。同时，运用LS/SA对C101算例进行求解，DBSCAN/SAVN与LS/SA求解C101的收敛过程对比如图6所示。

从图6可知，DBSCAN/SAVN的收敛速度优于LS/SA，DBSCAN/SAVN迭代到500～600次时，已获得最优路径，而LS/SA迭代到900～1100次时，才出现收敛趋势，迭代次数达到1500次时，最优路径的长度才趋于稳定，收敛速度较慢。从图上也可以明显看出，DBSCAN/SAVN的最优值优于LS/SA，路径长度值在迭代的过程中没有产生剧烈波动，因此DBSCAN/SAVN求解精度与稳定性优于LS/SA。

整理DBSCAN/SAVN和LS/SA算法在求解C101算例过程中获得的全局最优解，根据最优解绘制出路线图，DBSCAN/SAVN求解C101的最优解路线如图7所示，LS/SA求解C101的最优解路线如图8所示。对比图7与图8，LS/SA的最优路线图中的路径间还存在较多交叉点。根据表1中得到的数据，在数据规模为100的C101算例中，LS/SA的车辆使用数与总距离明显大于DBSCAN/SAVN的求解结果，验证了DBSCAN/SAVN的求解质量较优。

根据DBSCAN/SAVN求解C101获得的全局最优解，生成DBSCAN/SAVN求解C101最优解的配送路线，如表3所示。从每辆车的配送路径可知，车辆在满足车辆载重约束和时间窗约束的同时，所服务的顾客数量相差不大，说明车辆的载货任务分配较为均匀，配送路径规划较优。

表3 DBSCAN/SAVN求解C101最优解的配送路线

4 结束语

本文针对车辆路径问题中的经典问题——带时间窗的车辆路径问题(VRPTW)，提出了一种基于聚类的变邻域模拟退火算法(DBSCAN/SAVN)来实现VRPTW的求解。DBSCAN/SAVN算法通过DBSCAN聚类对顾客数据进行预处理，降低了后续SAVN算法的求解难度，在保证可以获得全局最优解的基础上，提高了SAVN算法的收敛速度。为了提高DBSCAN/SAVN中SA算法跳出局部最优解的能力，使用了exchange、insertion和2-opt三种扰动算子构造SAVN的邻域结构。通过仿真实验发现DBSCAN/SAVN在求解结果与算法运行时间上明显优于LS/SA、LNS/GA与MMAS。DBSCAN/SAVN的算法框架使子算法SAVN的执行次数增多导致运行时间稍长。下一步将通过分布式计算来缩短运行时间。在以后的研究中，可以尝试将机器学习、智能算法与精确算法结合使用，使用机器学习对数据进行分析并降低数据的维度，在此基础上使用智能算法求解得到最优解的集合，最后使用精确算法在集合中找到全局最优解。