挠性航天器动力学建模的非约束模态频率分析
2020-11-19沙建波戈新生
沙建波,戈新生
(北京信息科技大学 机电工程学院,北京 100192)
0 引言
近年来,随着载人航天工程、嫦娥探月工程和空间站计划的稳步推进,我国航天技术取得了长足的进步。航天技术的飞速发展对动力学与控制基础理论研究提出了新的挑战和进一步超前发展的需求。
传统航天器往往具有中心刚体平台,根据任务需要加装天线和太阳帆板等,这种航天器挠性附件的转动惯量和质量占整星的比重较小,一般使用约束模态对挠性航天器进行建模[1]。由于这类航天器具有相互耦合的刚体运动和挠性体弹性振动,是典型的刚柔耦合多体系统。挠性航天器动力学建模方法研究是挠性多体系统动力学的重要分支,20世纪70年代起,航天器的挠性结构振动问题日益引起人们的重视[2]。
Likins[3]利用集中参数模型表示挠性体,使用弹簧和阻尼器来模拟挠性效应,采用多刚体动力学的理论和方法建立了相应的挠性航天器动力学模型。同时期,Modi[4]也进行了相关研究。国内关于挠性多体系统动力学的研究起步于20世纪 80 年代,陆佑方[5]、洪嘉振等[6]通过专著的形式,对挠性多体系统动力学的基础理论和方法及其在航天器和机械臂等工程领域中的应用做了比较系统的介绍。刘莹莹等[7]建立了携带多个挠性附件卫星的动力学方程并分析了挠性附件对卫星姿态的影响。白圣建[8]等利用混合坐标法建立了带有大型挠性附件的卫星的一次近似动力学模型,分析了挠性附件横向和纵向变形的二次耦合项对大范围姿态机动的挠性卫星的刚柔耦合动力学特性的影响。胡庆雷[9]将挠性航天器简化为中心刚体—柔性梁系统,使用悬臂梁模态离散航天器柔性附件变形,采用混合坐标方法描述系统运动,建立了柔性航天器的动力学模型。章仁为[10]采用约束模态法建立了挠性航天器动力学模型,同时考虑了姿态耦合特性和位置耦合特性。随着航天科技的发展,挠性结构尺寸和重量逐渐增加,因此挠性化成为现代航天器的一大特点。Hablani[11]指出非约束模态建模和约束模态建模的刚柔惯量比较小时,约束模态法建立的动力学模型有比较大的误差。而非约束模态方法描述的是中心刚体不固定、挠性附件无阻尼的自由振动过程,体现的是整个航天器的动力学系统频率特性,更接近航天器在轨实际飞行状况,但地面无法提供非约束模态试验环境[12]。为此,本文基于非约束模态建立挠性航天器的动力学方程,通过特征值分析计算系统非约束模态固有频率,并与有限元分析对比,考察中心刚体和太阳帆板的质量比对系统的固有频率的影响。本文的研究结果可为大型挠性航天器动力学特征值问题提供一种理论依据。
1 挠性航天器动力学建模
图1所示为中心刚体带挠性附件的挠性航天器,B0表示航天器中心刚体,B1表示与中心刚体连接的挠性附件,其中点P为挠性附件B1与中心刚体B0的连接点。O-XYZ为轨道坐标系,Ob-XbYbZb为星体坐标系,P-XAYAZA为中心刚体与挠性附件联结的附件坐标系。
设点d为挠性附件上任意一点变形位移后所在位置。则附件上点d在坐标系O-XYZ下的矢径
r1=r0+rb+ra+δ
(1)
式中:r0为轨道坐标系原点到航天器质心Ob的矢径;ra为附件上一点到连接点P的矢径;rb为点P到航天器质心Ob的矢径;δ为附件上某一点的弹性变形。
对式(1)在轨道坐标系求导可得挠性附件上d点在惯性系的速度表达式
(2)
式中ω为星体系相对于轨道坐标系的旋转角速度。
通常情况下,各个量是在不同坐标系下度量的,因此需要将各个量转换到同一坐标系下度量。可以得到挠性附件上d点的速度在附件坐标系P-XAYAZA下的表达式
(3)
中心刚体上任意一点c到O的矢径
rc=r0+rd
(4)
将其转换到轨道坐标系上度量,则中心刚体上一点c的速度表达式为
(5)
挠性航天器的动能T分为两部分:中心刚体的动能Tb和附件的动能Tp,则挠性航天器的动能为
(6)
式中:Mb为中心刚体质量;Jb为中心刚体相对于轨道坐标系的转动惯量。
挠性航天器的势能主要来源于附件的弹性变形,则附件的变形势能
(7)
式中K为附件的刚度矩阵。若用模态坐标来描述附件的弹性变形δ,则δ可表示为
δ=Φη
(8)
式中:Φ为附件的模态函数;η为附件的模态坐标。
将式(8)代入式(6)和(7)中,可得到动能与势能的模态坐标表达式分别为
(9)
(10)
Λ=diag[ω12,ω22,…,ωN2]
(11)
根据拉格朗日方程
(12)
式中L=T-U。将式(9)和(10)代入式(12)中,进行简化整理可得
(13a)
(13b)
(13c)
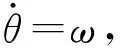
(14a)
(14b)
(14c)
方程(14)可以写成矩阵形式
(15)
式中
求解式(15)可得其特征方程为
(ΛM-K)Φ=0
(16)
通过求解方程(16)可得航天器非约束模态固有频率。
2 模态频率计算分析
2.1 挠性梁质量对固有频率的影响
将挠性航天器模型简化为中心刚体单侧挠性梁模型,分析计算挠性梁质量对固有频率的影响。所采用的中心刚体单侧挠性梁系统参数为:中心刚体边长R=0.5 m,转动惯量[14]Jr=100 kg/m2;挠性梁长度分别为l=4 m、8 m、12 m、16 m和20 m,挠性梁横截面积Af= 1.459 7×10-4m2,挠性梁截面惯性矩If=8.218 9×10-9M4;挠性梁材料密度ρ=2.766 7×103kg/m3,挠性梁杨氏弹性模量[7]Ef=6.895 2×1010Pa。因为挠性梁为等截面且材料密度为常量,因此挠性梁质量与挠性梁长度成正比。分别采用方程(16)所给出的非约束模态频率方程与有限元模型计算进行对比,数值计算结果如表1至表5所示。
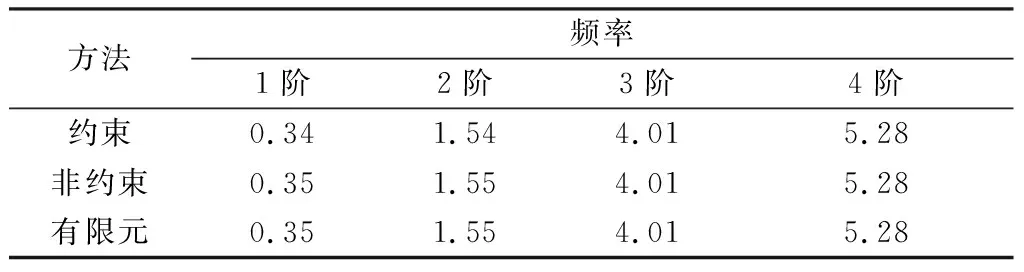
表1 l=4 m时中心刚体-挠性梁前4阶系统频率 rad/s

表2 l=8 m时中心刚体-挠性梁前4阶系统频率 rad/s
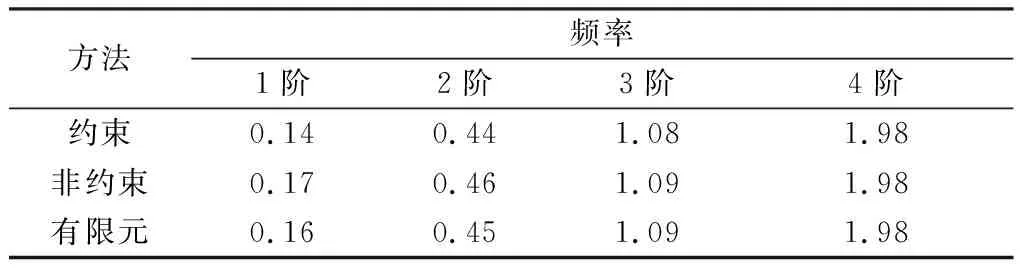
表3 l=12 m时中心刚体-挠性梁前4阶系统频率 rad/s
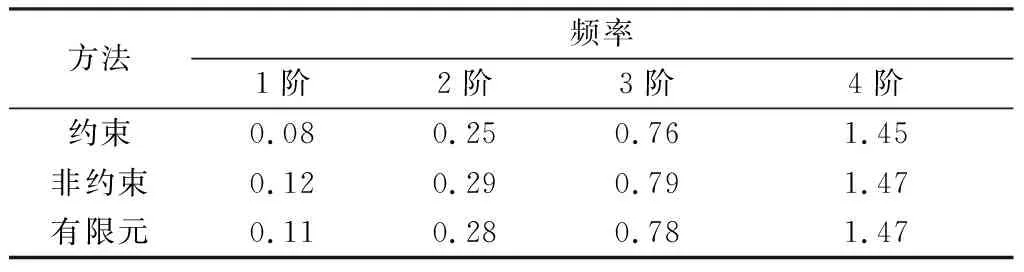
表4 l=16 m时中心刚体-挠性梁前4阶系统频率 rad/s

表5 l=20 m时中心刚体-挠性梁前4阶系统频率 rad/s
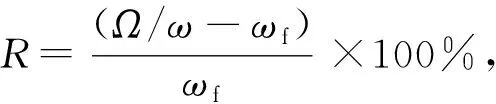
由表1至表5可以看出,当挠性梁长度分别为4 m、8 m、12 m时,约束模态方法和非约束模态方法计算结果与有限元仿真计算结果相近。挠性梁长度增加(对应质量增加)至16 m、20 m时,约束模态法计算结果相较于有限元仿真计算结果误差明显增大,尤其是在第1阶模态出现较大误差,约束模态所求第1阶固有频率的最大相对误差为28.6%。非约束模态法计算结果与有限元仿真结果基本一致,最大相对误差为9.1%。当挠性梁尺寸远大于中心刚体尺寸时,中心刚体质量在整个航天器系统中占比较小,使用约束模态法计算整个系统的固有频率时误差大,计算精度低,已无法反应系统整体的固有频率。而使用非约束模态法所求固有频率计算结果误差较小,计算精度高,与有限元仿真计算结果近似。
2.2 系统质量比对固有频率的影响
以中心刚体和单侧梁组成的系统模型为研究对象,仍采用2.1节中所选系统参数,选取l=20 m,改变中心尺寸大小,即改变其质量,分析中心刚体和挠性梁的质量比对系统固有特性的影响。取中心刚体质量mt与挠性梁质量mf比值分别为15,5,2.5,1,0.5,0.1。利用系统特征方程求解系统的固有频率,以ANSYS有限元仿真分析软件所求计算结果为参考依据,对比分析非约束模态法和约束模态法的适用范围和差异性,如表6至表11所示。
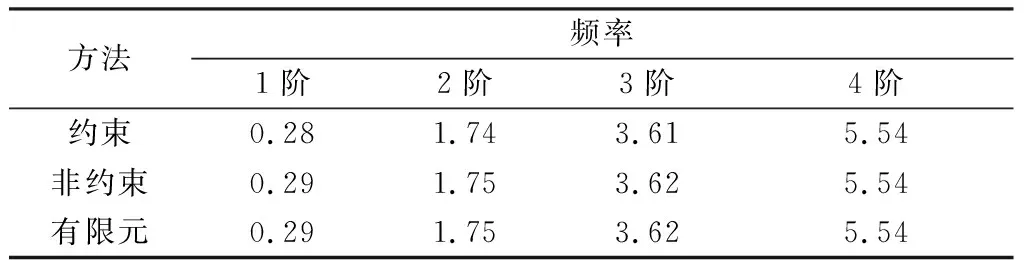
表6 质量比值mt/mf≈15系统频率 rad/s
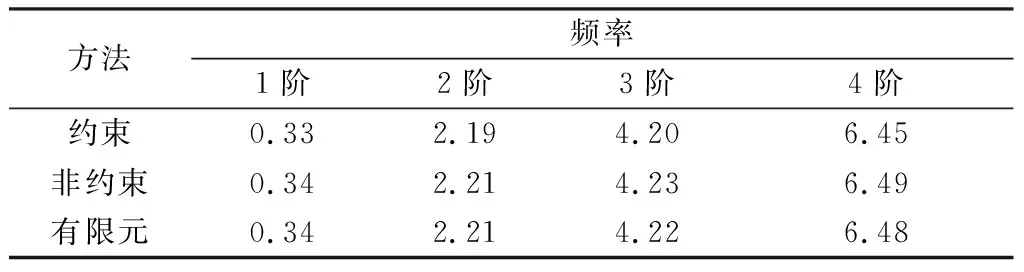
表7 质量比值mt/mf≈5系统频率 rad/s
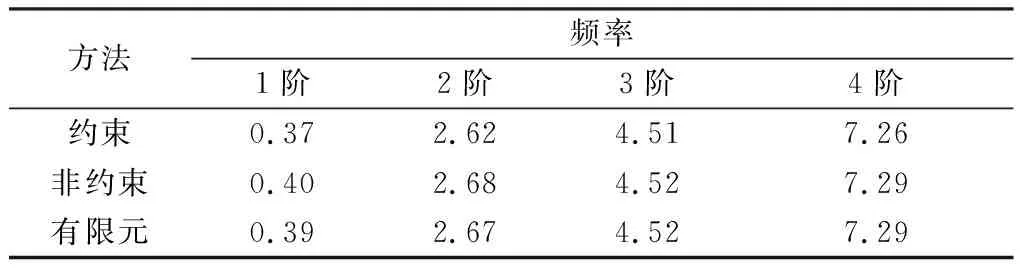
表8 质量比值mt/mf≈2.5系统频率 rad/s

表9 质量比值mt/mf≈1系统频率 rad/s
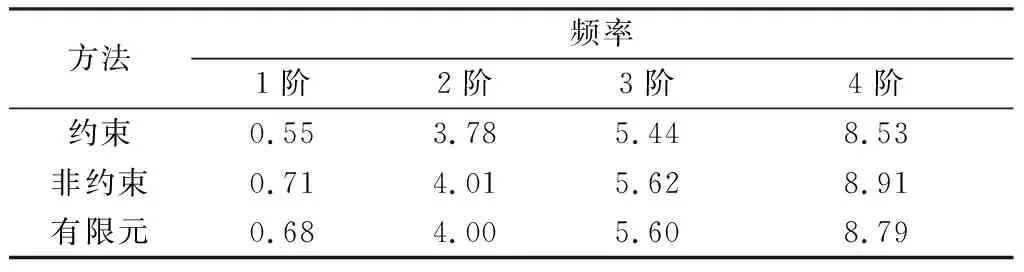
表10 质量比值mt/mf≈0.5系统频率 rad/s
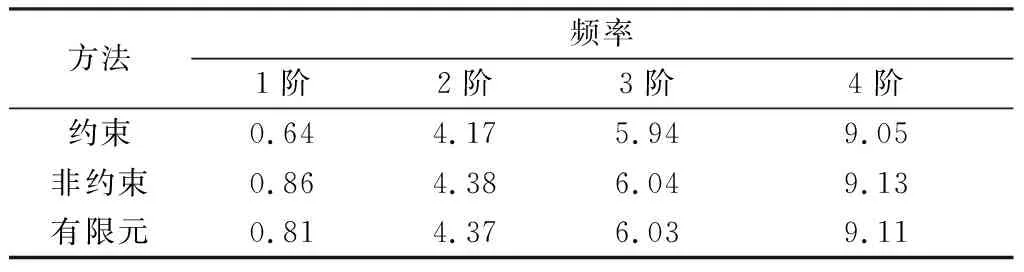
表11 质量比值mt/mf≈0.1系统频率 rad/s
从表6至表11可以看出,当中心刚体质量与挠性梁质量比值mt/mf大于或等于2.5时,约束模态所求固有频率的最大相对误差为7.5%,非约束模态所求固有频率误差较小,最大误差为2.59%。使用约束模态方法及非约束模态方法计算的固有频率均比较精确。若继续改变系统质量比,使中心刚体质量与挠性梁质量比值mt/mf≈1,即刚体质量与挠性梁质量相等,此时利用非约束模态方法计算的固有频率相对误差较小,最大相对误差3.85%,而约束模态所求固有频率,最大相对误差为17.31%。随着挠性附件质量的增加,当中心刚体质量与挠性梁质量比值mt/mf≈0.5时,约束模态方法所求系统频率相对误差较大,最大误差为19.12%,而非约束模态法计算结果与有限元结果基本一致,最大误差为4.41%。当中心刚体质量与挠性梁质量比值mt/mf≈0.1时,此时,中心刚体质量远小于挠性附件质量,约束模态方法计算的固有频率的最大相对误差为20.98%,非约束模态方法计算结果最大误差为6.17%。由此可知,当中心刚体质量远小于挠性附件质量时,使用非约束模态法所求系统固有频率与有限元方法计算结果基本一致,而约束模态方法计算出的固有频率与有限元方法计算结果误差较大。
考虑一种特殊情况,即当中心刚体质量与挠性梁质量比值mt/mf趋于零时,中心刚体质量mt趋向于无穷小,此时,系统模型可以近似简化为挠性梁,易于构建模型。如表12所示,非约束模态法所得固有频率最大误差出现在第1阶固有频率,最大误差为8.9%,误差较小,非约束模态动力学方程计算结果与有限元方法计算结果基本吻合。所以在这种情况下仍可采用非约束模态方法,简化模型,建立挠性航天器动力学方程求得其固有频率。
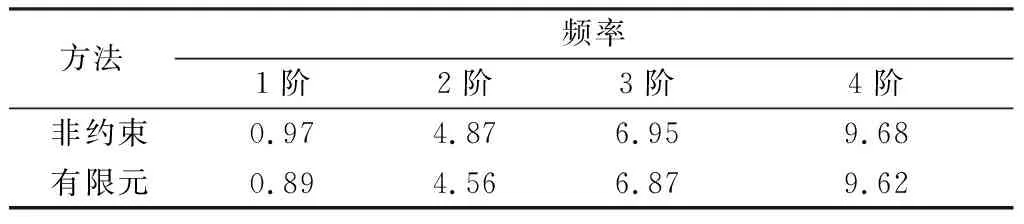
表12 系统简化为挠性梁模型前4阶系统频率比较 rad/s
3 结束语
本文利用拉格朗日法建立了挠性航天器系统的动力学方程,分别从约束模态和非约束模态建立航天器动力学模型。通过改变模型参数,利用非约束模态法所求固有频率与有限元仿真结果比较,验证了该方法的可行性。从挠性梁长度以及中心刚体挠性梁质量比两个方面出发,推导出约束模态和非约束模态的差异性和适用条件,并考虑了一种特殊情况,证明了非约束模态法是可行的。
