两类认知用户及信道聚合的认知无线网络研究

王浩炎，王玉玫

1.中国电子科技集团有限公司 第十五研究所 系统三部，北京100083

2.中国电子科技集团有限公司 第十五研究所 总体部，北京100083

1 引言

随着网络科技的发展，人们对无线互联的要求越来越高，尤其现在5G通信的应用和发展，对频谱的需求以及对动态接入和系统稳定性的需求越来越高。传统无线通信网络在网络信道资源分配上会造成很大的浪费，并且频谱利用率低下，因此认知无线电技术应运而生。

Mitola 等在1999—2000 年提出认知无线电（Cognitive Radio，CR）[1-2]。认知无线电思想的基本点是：无线通信电子设备具有认知功能，并可机会式工作在授权频段，增加频谱资源的利用率。

认知无线网络（Cognitive Radio Networks，CRn）[3]是继承认知无线电知识发展而来。认知网络指网络具有自主感知力，通过感知外界环境变化，自主学习理解，由目前的状况来计划、决定并采取行动，根据实际情况随时调整网络内部配置，自主决策，从而适应系统外部环境改变。其可以将传统静态频谱分配模式转换成动态自适应的模式，切实解决信道资源的不足，实现频谱的高效利用，满足当下通信发展趋势。认知无线网络的工作机理如图1。

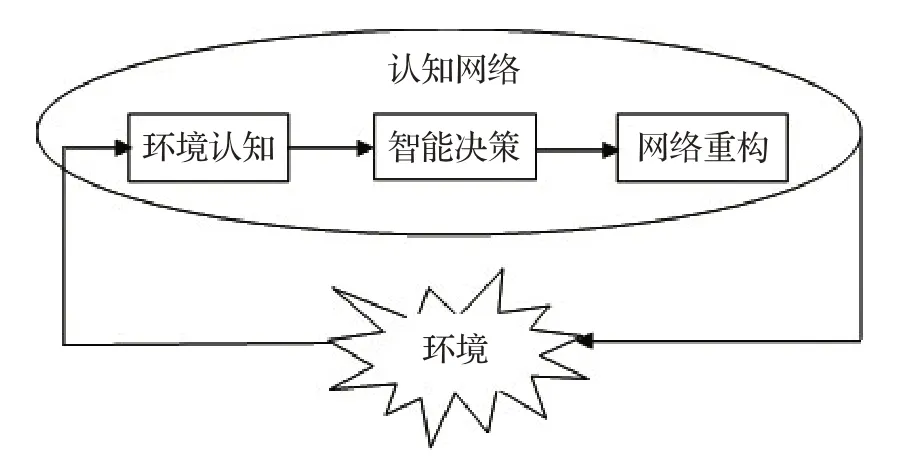
图1 认知网络工作机理

随着对认知无线电的深入研究，Motorola和Virginia Tech等公司提出认知无线网络这个概念。目前，很多研究都已经明确表明动态信道分配技术在多运营商环境下可行[4-5]，全球许多学者提出多种有效提高信道资源利用率的动态信道管理方法。

利用博弈论框架，Ewaisha等[6]提出最优停止规划的自适应信道选择策略，验证了关于信道分配的问题最后能收敛到确定的纳什均衡点。蒋兵霞在文献[7]中在博弈论基础上研究认知无线网络信道分配策略，基于潜在博弈理论框架分析频谱分配优化问题。王晓宇在文献[8]中讲述如何利用博弈论来研究认知无线网络的方法。

静态信道分配的用户无法去占用空闲信道，静态信道分配方式很大程度降低信道的利用效率。因此基于博弈论，又出现了在信道竞价拍卖基础上的动态信道分配算法。Chen 等[9]提出一种在干扰限制基础上的信道拍卖框架，授权用户遭遇到认知用户有限的干扰，结果证明该算法在认知无线网络的分散自适应学习环境中适用。Kasbekar 等[10]在此基础上提出一种信道拍卖框架。Toth 等[11]更多地引入经济学拍卖交易理论来研究信道频谱资源分配。

Akbar 等[12]利用隐马尔可夫模型，分析授权用户在连续多时间段的信道占用情况。Yao等[13]提出在信道感知中错误检测和错误报警条件下的动态信道分配机制。沈高青[14]针对认知无线网络饱和吞吐量构建二维马尔可夫链，达到认知用户的传输性被有效优化的目的。朱江等[15]提出一种基于隐马尔可夫模型的多信道功率博弈机制，从而保证更多用户达到传输速率需求。

分析上述文献可知，认知无线网络拥有传统网络所不具有的优势，在信道竞价拍卖基础上利用博弈论进行动态信道分配策略研究是当下国内外学者研究的热点，在具体模型构建上多采用排队论构建马尔可夫链模型对其进行研究。但是过去的研究往往只有授权用户与单类认知用户的博弈研究，缺少具体的动态信道聚合机制。随着通信的发展，两类以上认知用户及信道聚合机制的频谱分配策略是一个值得研究的方向。

认知无线网络是拥有自主认知功能的网络，通过分析实际具体的状态，规划、决策和响应以辨认当下网络状态。为实现提高端到端性能的目的，认知无线网络在一个自适应过程中学习，并可用于以后的决策。文献[16]对认知网络提供一个更全面的定义。理想型认知网络应具有前瞻性，在问题显示出来前可以自主尝试修改。另一方面，为支持未来网络架构和网络元素的变化，认知无线网络体系架构应具有可扩展性和灵活性。

本文提出一种基于两类认知用户及信道聚合机制的频谱分配策略。首先建立具有多优先级离散时间排队模型，构造三维马尔可夫链，得到马尔可夫链的转移概率矩阵。然后得到系统的稳态分布并进行分析，获得系统性能指标。最后对次级认知用户接入行为博弈优化，得到个人最优接入率和社会最优接入率等。

2 频谱分配策略模型及系统性能指标

2.1 工作机制

基于两类认知用户及动态信道聚合机制的频谱分配策略，即授权用户PU具有最高抢占优先权，高于认知用户，而认知用户有两种类型数据包，分别是高级认知用户SU1 和次级认知用户SU2，SU1 抢占优先权高于SU2。随系统中数据包个数改变，信道个数被中央控制器动态调整聚合。工作机制架构图如图2所示。

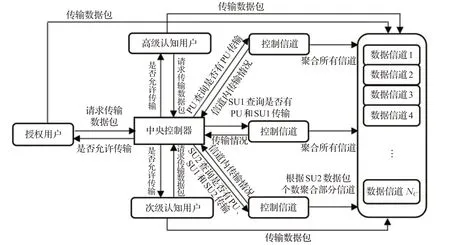
图2 工作机制

2.2 基于两类认知用户及信道聚合机制的频谱分配策略

设认知无线网络中单独一个授权频谱一般是由NC个数据信道和1个控制信道组成。在系统中，授权用户数据包PU有最高优先权，认知用户分两类数据包，分别是高级认知用户数据包SU1 和次级认知用户数据包SU2，SU1对SU2具有抢占优先权。PU数据包的传输可中断SU1和SU2数据包的传输，而SU1数据包的传输则可以抢占中断SU2数据包的传输。

为满足PU和SU1的响应性能，PU和SU1设置零缓存，而SU2 设置有限缓存，从而降低SU2 响应延迟。系统中没有数据传输时，为防止信道资源被浪费，所有信道不被激活。

当PU 对系统发出请求传输信号，而信道中没有其他PU，并且授权用户优先级最高时，全部信道都被中央控制器激活并绑定成一个新的聚合信道，新到达PU 在此聚合信道完成传输。假设信道中已有SU传输，则PU将抢占SU传输信道。

当SU1到达系统时，如系统被PU占据，则SU1离开系统，传输失败。如果系统内是SU1 占据聚合部分信道，则新到达SU1寻找另一个可绑定的新的聚合信道进行传输。如信道被SU2 占据，则中断SU2 传输，SU1 占据信道进行传输。

系统为SU2设置一个缓冲区，将准入门槛设置为一个接入阈值。系统中新到达一个SU2，假设此时SU2个数等于系统缓冲区的接入阈值，则新到达的SU2会阻塞系统。接入阈值也可以控制SU2 中断后的返回行为。当传输中的SU2被中断，如果缓冲区中的SU2个数小于接入阈值，则中断的SU2 会返回缓冲区，否则中断的SU2 就会离开系统，终止数据传输。这里假设中断的SU2对新到达的SU2具有较高优先级。

当系统中仅存在SU2时，部分信道被中央控制器激活绑定用于传输SU2。设系统内SU2 的个数来决定激活的信道个数，次级认知用户缓存量大小为K(K ＞0)，此时系统所能容纳的次级认知用户数据包的最大个数为K+1。当仅存在SU2 在系统传输时，即PU 和SU1的传输请求不存在，假设系统内SU2个数为G，则次级认知用户数据包个数与系统总容量的比率为G/(K+1)。系统内信道总数为NC,NC是整数，因此需被聚合绑定信道的个数用向上取整函数NCG/(K+1)来计算。

综上，一个PU 或一个SU1（相对于SU2）始终在由全部信道激活绑定的聚合信道上传输，在这两类数据包中，绑定聚合信道个数一直不变。相反，对SU2来说，一个次级认知用户数据包在部分信道绑定的聚合信道上传输，随到达系统的SU2 个数的变化，绑定信道个数随之变化。

2.3 基于两类认知用户带有可变服务率的系统模型

2.3.1 带有可变服务率的多优先级排队模型的建立

将时隙作为单位，系统模拟的建立是在离散时间领域中观察用户行为。举例，设时刻t=n，在时隙开始时，(n,n+)这个时间点数据包到达，在时隙结尾(n-,n)这个时间点数据包完成传输，然后从系统离开。

设数据包系统传输所需时间与数据包到达的间隔互不影响。令PU的到达遵循参数SU1、SU2 到达分别遵循参数和Bernoulli 过程。授权用户数据包和两类认知用户数据包在聚合信道上的传输时间的分布是几何分布。设在一个时隙内PU的服务率为μ1，SU1的服务率为μ21，SU2的服务率为μ22。

通过信道聚合机制的频谱分配策略可知，信道内SU2 数量和实际服务率联系密切。当仅有SU2 数据包存在系统内，假定该类数据包的个数为G，SU2的实际服务率为其表达式如式（1）所示：

为保证式（1）中ϑG的取值范围满足0 ＜ϑG＜1，假设SU2数据包在单个信道上的服务率服从0 ＜NCμ22＜1。

把聚合信道看成单服务台，假设次级认知用户为低优先级顾客，而高优先级顾客是授权用户和高级认知用户抽象成的，缓存空间则为次级认知用户的缓存，立足两类认知用户及信道聚合机制的频谱分配策略工作机制，可以构建一个带有可变服务率的具有多优先级和有限等待空间的排队模型。

令Ln=i(i=0,1,…,K+1)表示在时刻t=n+时，系统中数据包的总个数为i（包括授权用户PU、高级认知用户SU1和次级认知用户SU2）。令Pn=k(k=0,1)表示在时刻t=n+时，系统中PU 的个数为k 。令Sn=j(j=0,1)表示在时刻t=n+时，系统中SU1 的个数为j。则{Ln,Sn,Pn}就可以构成一个三维马尔可夫链，该三维马尔可夫链的状态空间Ω 可表示为式（2）。

式中，状态(i,0,0)表示有i 个数据包在系统里，且数据包都是SU2 数据包；(0,0,0)则表示没有任何数据包在系统里；状态(i,0,1)表示系统中有i 个数据包，其中1个数据包是PU的数据包，i-1 个数据包是SU2数据包；状态(i,1,0)表示系统中有i 个数据包，其中有1 个数据包是SU1，SU2个数为i-1。

2.3.2 带有可变服务率的多优先级排队模型的稳态分布

设P 为三维马尔可夫链{Ln,Sn,Pn}的状态转移矩阵，是一个(K+2)×(K+2)的块状矩阵，如式（3）。

对于式（3），矩阵的子块Pu,v是一步转移矩阵，含义是系统从水平u 转移到水平v，这里u=0,1,…,K+1，v=0,1,…,K+1，根据系统的不同水平，对各个子块具体分析如下所示：

（1）当系统处于u=0 水平状态时，在t=n+时刻，无任何种类数据包在系统内。在t=(n+1)+时刻，系统状态转移到水平v(v=0,1,2)。

当v=0 时，在时刻t=(n+1)+无数据包到达，此时P0,0详情见式（4）。

当v=1 时，在时刻t=(n+1)+，系统只含一个PU 或SU1或SU2，此时P0,1如式（5）。

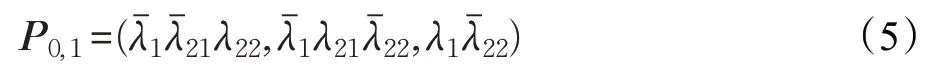
当v=2 时，在时刻t=(n+1)+，系统有一个PU 和SU2或有一个SU1和SU2，此时P0,2如式（6）。

（2）当1 ≤u ≤K-1(K ＞1)时，在时刻t=(n+1)+，系统内有u 个数据包，系统转移到水平v(v=u-1,u,u+1,u+2)。

当v=u-1 ，数据包在系统中的个数在时刻t=(n+1)+减少一个，则子块Pu,u-1的详细情况有两种，如下所示：

若u=1，Pu,u-1如式（7）。

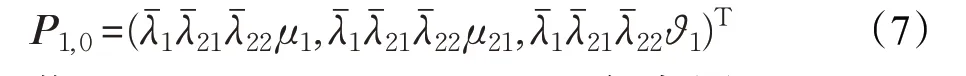
若2 ≤u ≤K-1 且K ＞2，Pu,u-1如式（8）。

在v=u 情况下，数据包在系统中的个数在时刻t=(n+1)+保持不变，子块Pu,u如式（9）。

在v=u+1 情形下，数据包在系统中的个数在时刻t=(n+1)+变多一个，子块Pu,u+1如式（10）。

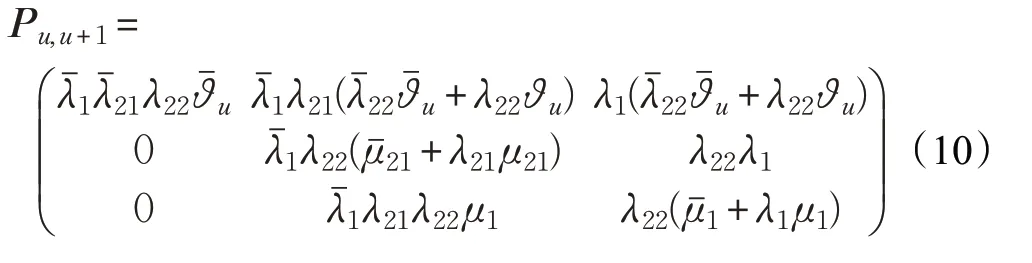
在v=u+2 情况下，数据包在系统中的个数在时刻t=(n+1)+变多两个，子块Pu,u+2如式（11）。

（3）在系统水平u=K 时，在时刻t=n+数据包在系统中的个数为K ，即次级认知用户缓存区仅剩一个空位且聚合信道已被占用，则时刻t=(n+1)+，系统转移到水平v(v=K-1,K,K+1)。

在v=K-1 情况下，数据包在系统中的个数在时刻t=(n+1)+减少一个，此时PK,K-1如式（12）。

在v=K 情况下，数据包在系统中的个数在时刻t=(n+1)+不变，则PK,K如式（13）。

在v=K+1 情况下，数据包在系统中的个数在时刻t=(n+1)+变多一个，此时子块PK,K+1如式（14）。

（4）当系统水平u=K+1 时，在时刻t=n+，数据包在系统中的个数为K ，即系统聚合信道已被占用，次级认知用户缓存区已满，则时刻t=(n+1)+，系统转移到水平v(v=K,K+1)。

在v=K 情况下，数据包在系统中的个数在时刻t=(n+1)+减少一个，则PK+1,K如式（15）。

在v=K+1 情况时，数据包在系统中的个数在时刻t=(n+1)+仍处于满的状态，则PK+1,K+1如式（16）。

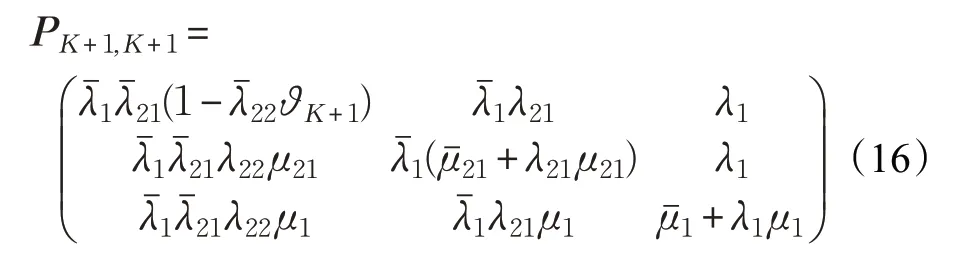
转移概率矩阵中的每个元素都可由式（4）到式（16）运算得出。

分析转移概率矩阵P 的结构，可得出三维马尔可夫链{Ln,Sn,Pn}的特性，即非周期、不可约、正常返。定义三维马尔可夫链的稳态分布πi,j,k如式（17）。

定义Π 为系统的稳态概率向量，Π=(Π0,Π1,…,Πk+1)。由平衡方程和正规化条件可得式（18）。

其中e 为列向量。

定义Πi为系统处在i 水平的概率向量，Πi如式（19）。

通过高斯-赛德尔方法，可得到稳态分布Π。

2.4 系统性能指标

为更好更全面地评价使用以两类认知用户及信道聚合机制为基础的频谱分配策略的系统呈现出的性能优缺点，模拟一个性能指标体系，该指标体系由次级认知用户SU2 的吞吐量θ、阻塞率β、中断丢失率γ 及平均延迟时间δ 等组成。

2.4.1 次级认知用户阻塞率

次级认知用户SU2 的阻塞率β 表示在系统中每个时隙内被阻塞的次级认知用户SU2 数据包个数。新到达次级认知用户数据包因系统缓存区已满，绑定聚合信道正被用户占用传输数据，而占用信道的用户在该时隙内不会离开系统，因此该次级认知用户数据包无法传输，该现象称为次级认知用户的阻塞。β 的表达式如式（20）。

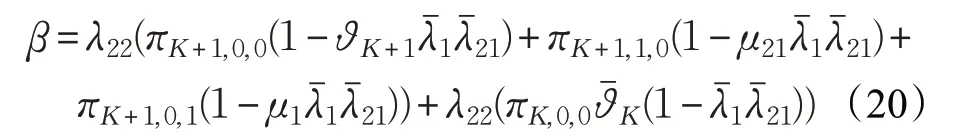
2.4.2 次级认知用户中断丢失率

由于次级认知用户缓存区已被占满，正在绑定聚合信道中传输的次级认知用户数据包，其传输信道被刚到的授权用户或高级认知用户数据包强占，该包被丢弃，称中断丢失。单位时隙内丢失的次级认知用户数据包数量便是次级认知用户丢失率γ，表达式如式（21）。

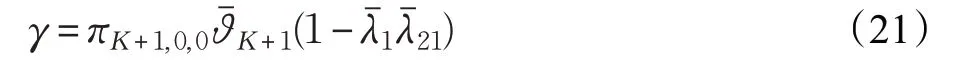
2.4.3 次级认知用户吞吐量

次级认知用户数据包在系统中一个单位时隙内完成传输的个数就是次级认知用户吞吐量θ,表达式如式（22）。

2.4.4 次级认知用户平均延迟时间

次级认知用户从加入系统传输到离开系统经历平均时间长度是次级认知用户平均延迟时间δ，据排队论系统的Little 定理[17]给出次级认知用户平均延迟时间δ表达式，如式（23）。

3 系统性能数值实验分析

数值实验分两次模拟操作：第一次，在聚合信道数量不一样情况时，次级认知用户数据包吞吐量、阻塞率、中断丢失率以及平均延迟时间等随次级认知用户数据包在系统中的个数变化而改变的趋势。第二次，通过设置多组不同参数，分析次级认知用户缓存容量对次级认知用户的中断丢失率、阻塞率、吞吐量以及平均延迟时间的影响。参数公式设置如表1。

表1 公共参数

3.1 次级认知用户阻塞率变化趋势

图3刻画了当授权用户数据包到达率λ1=0.1，高级认知用户数据包到达率λ21=0.2，次级认知用户到达率λ22=0.2 时，随信道个数NC的变化，次级用户阻塞率β的变化。如图所示，在信道聚合机制下，信道个数为NC时，次级认知用户阻塞率β 随次级认知用户缓存容量变大会下降。其他变量固定情况下可看到随信道个数NC增大，次级认知用户阻塞率下降，因刚进入系统的次级认知用户被传输概率随绑定信道个数变多而增加，阻塞率下降。

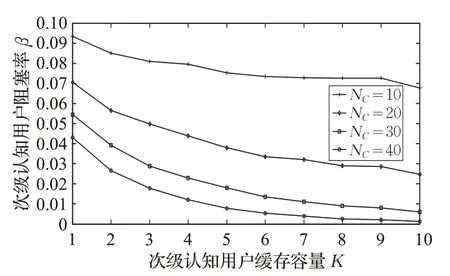
图3 次级认知用户阻塞率变化趋势I

图4 刻画了信道个数NC=40 时，随着用户数据包到达率变化，次级认知用户阻塞率β 的变化。如图所示，当次级认知用户与高级认知用户到达率一定时，次级认知用户阻塞率会随授权用户到达率的增加而增加，当次级认知用户与授权用户到达率一定时，次级认知用户的阻塞率随着高级认知用户的到达率增加而逐渐增加。而当高级认知用户与授权用户到达率一定时，次级认知用户阻塞率会随其到达率的增加而继续增加。

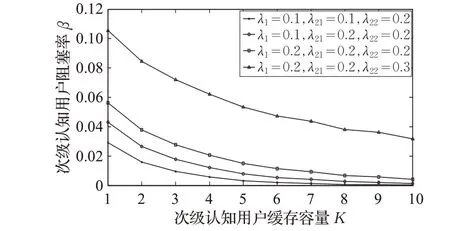
图4 次级认知用户阻塞率变化趋势II

3.2 次级认知用户吞吐量变化趋势

图5 刻画了当授权用户到达率λ1=0.2，高级认知用户到达率λ21=0.2，次级认知用户到达率λ22=0.2 时，随信道个数NC的变化，次级认知用户吞吐量θ 的变化。如图所示，在动态信道聚合机制下，信道个数为NC时，随次级认知用户缓存容量增大，次级认知用户的吞吐量θ 会逐步增加并趋于稳定。也可看到，在其他变量固定情况下，次级认知用户吞吐量会随信道个数NC的逐渐增大而增加。

图5 次级认知用户吞吐量变化趋势I

图6 刻画了当信道个数NC=30 时，随各个用户数据包到达率变化，次级认知用户吞吐量θ 的变化。如图所示，当高级认知用户与次级认知用户到达率一定时，次级认知用户吞吐量会随授权用户到达率增加而减小。当授权认知用户与次级认知用户到达率一定时，随高级认知用户到达率的增加，次级认知用户吞吐量减小。而当高级认知用户与授权用户到达率一定时，次级认知用户吞吐量会随其自身到达率的增加而增加。

3.3 次级认知用户中断丢失率变化趋势

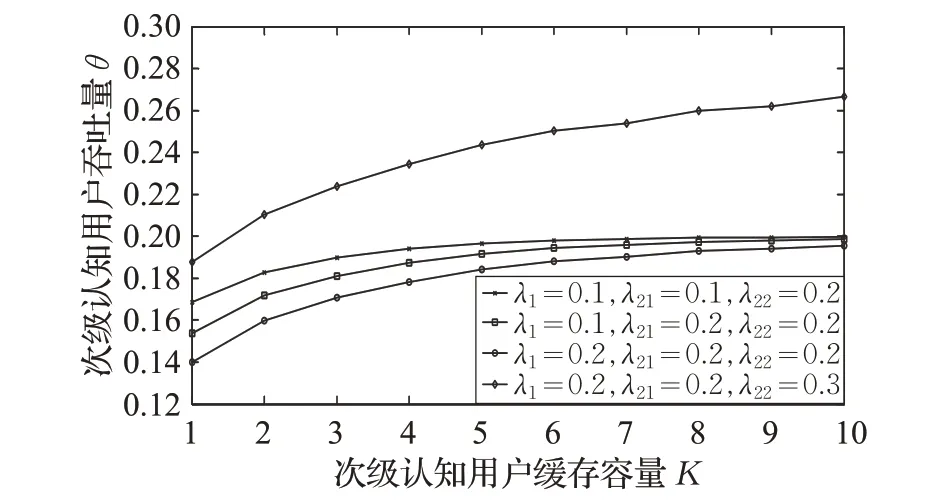
图6 次级认知用户吞吐量变化趋势II

图7 刻画了当授权用户到达率λ1=0.2，高级认知用户到达率λ21=0.2，次级认知用户到达率λ22=0.2 时，随信道个数NC的变化，次级认知用户中断丢失率γ 的变化。如图所示，在动态信道聚合机制下，信道个数为NC时，随次级认知用户缓存容量增大，次级认知用户中断丢失率γ 逐渐减少并下降逐渐趋于平缓。也可看到，在其他变量固定情况下，随信道个数NC减小，次级认知用户中断丢失率增大。

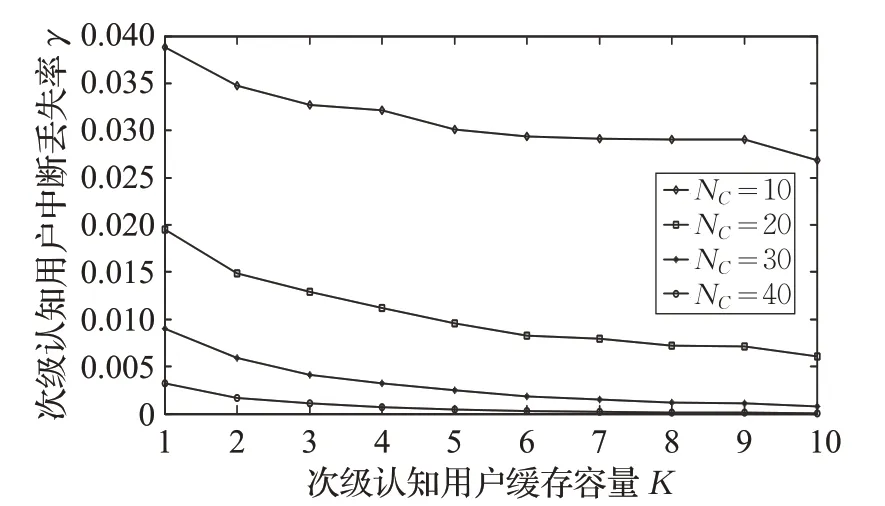
图7 次级认知用户中断丢失率变化趋势I

图8 刻画了在信道个数NC=10 情况下，随各个优先级用户数据包到达率的变化，次级认知用户中断丢失率γ 的变化。如图所示，在动态信道聚合机制下，在信道个数NC=10 情况下，三种优先级别用户数据包到达率的改变都会影响次级认知用户中断丢失率的大小变化。当高级认知用户与次级认知用户到达率一定时，次级认知用户中断丢失率就会随授权用户到达率增加而逐渐增大。而当授权认知用户与高级认知用户到达率一定时，次级认知用户中断丢失率也随次级认知用户到达率增加而逐渐增加。

图8 次级认知用户中断丢失率变化趋势II

3.4 次级认知用户平均延迟时间变化趋势

图9 刻画了在授权用户到达率λ1=0.2，高级认知用户到达率λ21=0.2，次级认知用户到达率λ22=0.2 情况下，随信道个数NC变化，次级认知用户平均延迟时间δ 的变化。如图所示，在动态信道聚合机制下，在同一信道个数NC情况下，随次级认知用户缓存容量增加，意味着排队等待传输的次级认知用户数据包个数变大，每个次级认知用户平均等待时间会增加，其平均延迟时间会增加。也可看到，在其他变量固定情况下，随信道个数NC减小，次级认知用户平均延迟时间增大。

图9 次级认知用户平均延迟时间变化趋势I

图10 刻画了当信道个数为NC时，随各个优先级用户数据包到达率的变化，次级认知用户平均延迟时间δ的变化。如图所示，在高级认知用户与次级认知用户到达率不变情况下，次级认知用户平均延迟时间会随授权用户到达率增加而增大，在次级认知用户与授权用户到达率不变情况下，次级认知用户平均延迟时间会随高级认知用户到达率增加而变大。当高级认知用户与授权用户到达率一定情况下，次级认知用户平均延迟时间基本不会随次级认知用户到达率增加而变化，当次级认知用户缓存量一定时，次级认知用户延迟时间不会被次级认知用户到达率影响而产生变化。

图10 次级认知用户平均延迟时间变化趋势II

4 针对次级认知用户接入率的优化分析

本文采用一系列博弈论来研究次级认知用户的接入行为，为保证自身利益的最大化，研究次级认知用户应该产生什么样的反应。第一步，为得到次级认知用户数据包的均衡接入率，分析次级认知用户数据包的纳什均衡[18]接入行为；第二步，为达到社会最优化目标，使社会收益最大，分析次级认知用户的社会最优接入率；最后，为使次级认知用户遵循社会最优，给出最优定价方案。

4.1 优化假设

给出一些分析中必须使用的优化假设：

（1）在进入系统时，一个次级认知用户数据包可以选择是否接入其中，但是它对系统内部详细情况在做出决定以前并不了解。在这之外，次级认知用户数据包在接入系统以后，不能自己退出系统。

（2）一个次级认知用户可获得收益a1在其接入并在系统传输成功以后。

（3）系统可能在一个次级认知用户数据包进入系统选择接入以后强制其在成功传输之前离开系统或将其阻塞。定义一次尝试是一个次级认知用户数据包进入系统中并做出选择接入这个决定的行为，引入代价a2(a2＜a1)来表示次级认知用户数据包每一次尝试。

（4）假设Λ 表示次级认知用户数据包的潜在到达率。

对于一个次级认知用户数据包来说，要不要做出接入系统这样一个尝试是其核心问题。设一个次级认知用户数据包尝试接入系统的概率q0(0 ＜q0＜1)表示次级认知用户数据包接入策略。

4.2 纳什均衡策略

系统成功传输一个次级认知用户数据包概率表示为ε(λ22)，如式（24）。

式中，β 表示次级认知用户数据包阻塞率，γ 表示次级认知用户数据包中断丢失率，λ22是次级认知用户的到达率。

如式（25）所示，选择接入系统的次级认知用户数据包的定义表示为个人收益函数W1(λ22)。

分析纳什均衡理论，假设均衡接入概率定义为qε，表示次级认知用户数据包接入系统的概率，将均衡接入率使用λε=qεΛ 表示。任何一个次级认知用户数据包在接入系统时都不能违背均衡接入概率qε和纳什接入率λε。

设NC=15,Λ=0.5,a1=3,a2=2，在不同的授权用户服务率μ1和次级认知用户数据包缓存容量K 情况下，分别做出个人收益函数W1(λ22)随次级认知用户数据包到达率λ22改变而改变的变化曲线，如图11所示。

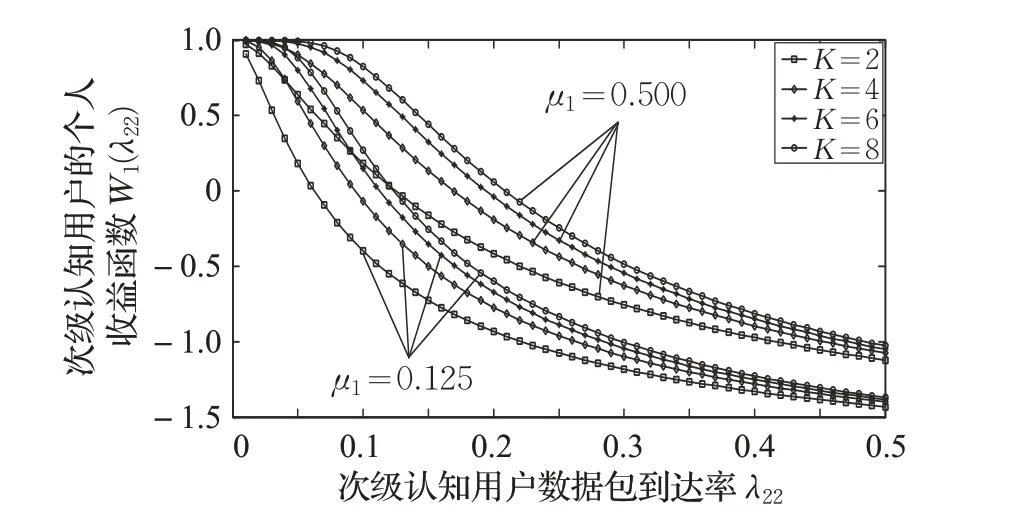
图11 个人收益函数变化趋势

图11 可知，个人收益W1(λ22)随次级认知用户数据包到达率λ22增大而单调下降。分两种情况：

（1）在W1(Λ)≥0 情况下，无论哪种情况此时次级认知用户的收益全部非负。在qε=1 均衡策略下，均衡接入率为λε=qεΛ=Λ。

（2）在W1(Λ)＜0 情况下，次级认知用户的收益总是为负。在所有的次级认知用户数据包选择接入系统时，W1(0+)＞0，一个选择尝试接入系统的次级认知用户数据包获得收益在qε=0 时为正，显然不尝试接入系统的结果没有这个结果好。相反，有一个选择尝试接入系统的次级认知用户数据包获得的收益在qε=1 的情况下为负。纳什均衡在qε=1 与qε=0 这两种情形下都达不到。可通过分析纳什均衡理论，得出一个均衡接入概率，其表达式为qε=λε/Λ ，其中有一均衡点使方程W1(λε)=0 成立，其为均衡接入率λε。

表2 表示个人最优策略下均衡接入率λε与均衡接入概率qε的数值结果。

表2 个人最优策略下的数值结果

如表2所示，当μ1=0.500 和K=2 时，W1(λε)=0 的λε的解在[0.12，0.13]范围内，观察图11可以发现。因此将0.12作为均衡接入率下限值，0.13作为均衡接入率上限值。根据qε=λε/Λ，将标记0.24作为均衡接入概率下限值，标记0.26作为均衡接入概率上限值。

4.3 社会最优策略

根据个人收益函数表达式，通过分析给出社会收益函数W2(λ22)表达式，如式（26）。

其中，ε(λ22)表示一个次级认知用户数据包在系统中被成功传输概率。

设NC=15,Λ=0.5,a1=3,a2=2 ，图12 刻画了在不同的授权用户服务率μ1和次级认知用户数据包缓存容量K 情况下，社会收益函数W2(λ22)随次级认知用户到达率λ22的变化趋势。

图12 可知，社会收益函数W2(λ22)随次级认知用户数据包到达率λ22增加，其变化趋势显示出一个上凸走向。总是会有一个最优次级认知用户数据包到达率可达到最优社会收益函数。

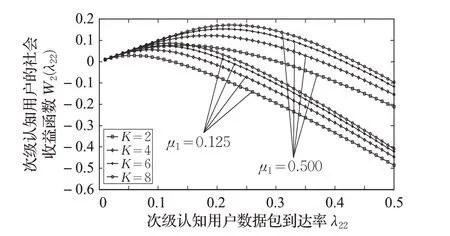
图12 社会收益函数变化趋势

如式（27），存在社会最优接入率λs使得社会收益达到最大值。

推导社会最优均衡接入概率qs，如式（28）。

本文给出了社会最优接入率λs和社会最优接入概率qs的数值结果，如表3。

表3 社会最优策略下的数值结果

通过将表3 中社会最优策略下接入率与接入概率的数值和表2 中纳什均衡策略下接入率与接入概率的下限值观察比较，得出社会最优策略下的社会最优接入概率qs小于纳什策略下的均衡接入概率qε，社会最优接入率λs也小于均衡接入率λε，纳什均衡理论正好和这一现象吻合。系统中将会出现更多的次级认知用户数据包在纳什均衡理论下选择接入，不合人意的是社会收益会因此下降。因此，为降低次级认知用户数据包接入率并保证尽可能最大化社会收益，试着让那些选择接入系统的次级认知用户数据包缴纳一定接入费用。

4.4 定价方案

基于两类认知用户及信道聚合机制的频谱分配策略，假定中央处理器能成为一个收费者形象，可让每个选择接入系统的次级认知用户数据包缴纳一定的费用f 。

在一个尝试接入系统的次级认知用户数据包被中央控制器收取费用f 以后，得到一个表达该次级认知用户数据包收益WP(λ22)的式（29）：

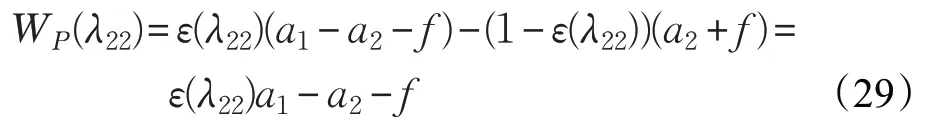
社会最优的目标就是使系统中的次级认知用户与中央控制器总体的一个收益最大化。对社会收益函数（考虑到接入费用f）重新做出定义，记作Ws(λ22)，如式（30）：

发现引入接入费用以后重新定义社会收益函数Ws(λ22)与未引入接入费用时社会收益函数W2(λ22)的表达式一样，说明两者不管收不收取接入费用，社会收益一样。接入费用主要产生自中央控制器之上，不会影响社会最优策略的结果。

在式（30）中，设置λ22=λs，通过计算方程WP(λs)=0可以得到接入费用f 的表达式。

当λs＜Λ 时，接入费用f 表达式如式（31）所示。

观察表4中社会最优接入率λs并分析其数值结果，在不同的参数设置下表4 给出了接入费用f 的数值结果。表4中接入费用“ f ”估计到小数点后4位。

表4 接入费用的数值结果

5 结束语

为了让系统得到更稳定的性能，本文提出一种基于两类认知用户及信道聚合机制的频谱分配策略。与传统静态信道或者单信道以及只有一类认知用户的研究不同，本文考虑两类认知用户及基于系统中数据包的个数动态激活聚合信道。首先根据提出的工作机制，构建三维马尔可夫链，为得到系统转移概率矩阵并进行稳态分析，构建多优先级带有可变服务率的离散时间排队模型。之后通过系统稳态分布进一步分析，得出性能指标。其次主要对性能指标展开分析，构建表达式并进行数值实验，论证所提出的基于两类认知用户及动态聚合机制的频谱分配策略在稳定系统性能和节省网络资源方面的有效性。最后博弈分析次级认知用户的接入行为，分析立足于社会整体优化方面的社会最优策略和以个体优化方面为基础的纳什均衡策略，在此基础上提出一个定价方案，从而实现社会最优。

本文仅考虑两类认知用户，并提出一种基于两类认知用户及动态信道聚合机制的频谱分配策略，但随着网络的发展，尤其是5G 网络的普及，基于N 类认知用户的认知无线网络的研究将是必然趋势。