执行器失效的有限时间输出跟踪控制

王力梅，霍丽芳

(1.天水师范学院 数学与统计学院，甘肃 天水 741000；2.河北建筑工程学院 数理系，河北 张家口 075000)

0 引 言

最近几年，由于切换系统在交通控制、智能机器人、化学控制等实际应用中的重要作用，许多人对切换系统进行了大量的研究[1-5]。切换系统是由有限个连续的或离散的子系统和一个切换率构成，切换率决定在切换时刻哪个子系统被激活。J.LIANG[6-7]将切换系统的有关结果推广到分数阶，研究了分数阶切换系统有限时间稳定性及输入输出有限时间稳定性。在许多理想的情况下，控制器和系统的切换是同步的。但是，在许多情况下，当控制器得到的切换信号延迟于系统的切换时，闭环系统会有一个异步的切换。显然，这种情况更具有真实性和研究的价值。同时，对于有些系统，研究短时间内的性能更具有理论和应用价值，H.LIU等[8]考虑了异步的有限时间H∞性能问题。输出跟踪控制问题也是许多人关注的热门话题，H.LIU等[8]利用平均驻留时间方法，讨论了有时变延迟的正切换系统的指数L1输出跟踪控制。

在真实的控制系统中，由于受到各种环境因素的影响，执行器失效是经常发生的。另外，研究稳定性是控制领域的一个热门话题，许多学者研究了时间趋于无穷时的渐进行为。在实际中，对于有些系统研究有限时间内的系统性能是非常必要的。因此，本文使用李雅普诺夫方法和平均驻留时间方法研究了考虑执行器失效下的有限时间输出反馈问题，得出执行器失效下的有限时间输出反馈控制的充分条件。

1 问题陈述

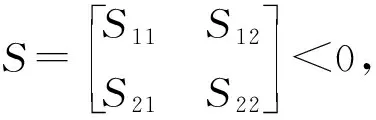
(1)

(2)

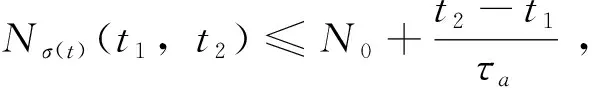
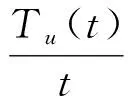
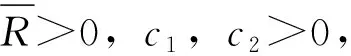
考虑如下系统

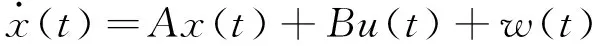
z(t)=Cx(t)

(3)

这里x(t)∈Rn是状态，u(t)∈Rp是控制输入，z(t)∈Rq是测量输出，{w(t)∈Rs|w(t)∈L2[0,∞)}是干扰输入，A、B、C是适当维数的常数矩阵。

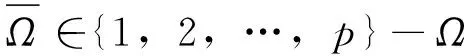
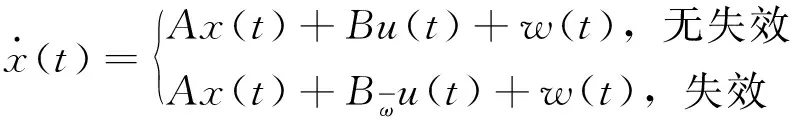
(4)

zr(t)=Grxr(t)

(5)

这里xr(t)∈Rn是参考状态,r(t)∈Rn是有界的参考输入信号，zr(t)∈Rq是参考输出，Ar是Hurwitz矩阵，Gr是适当维数的常数矩阵。

状态反馈控制器设计为

u(t)=Kx(t)+xr(t)

(6)

(7)

则系统(3)简化为如下的切换系统

z(t)=Cx(t)

(8)

其中A1=A2=A,B1=B,B2=Bω。

(9)

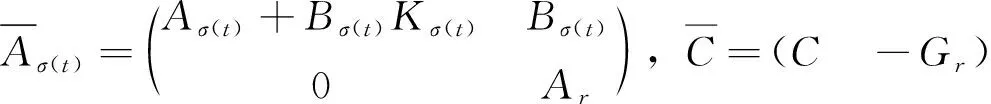
2 有限时间稳定性分析

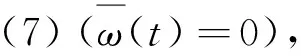
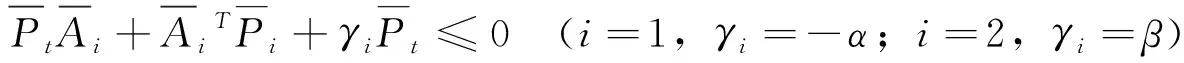
(10)

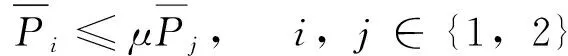
(11)

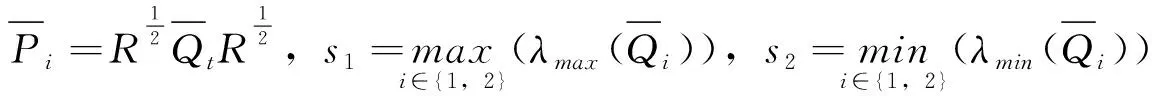
(12)

那么，在以下平均驻留时间机制下

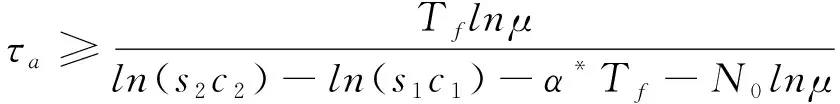
(13)

证明取李雅普诺夫函数

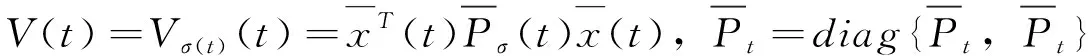
(14)

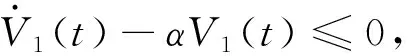
V1(t)≤eα(t-t0)V1(t0)

(15)

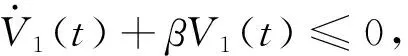
V2(t)≤e-β(t-t0)V2(t0)

(16)

假设执行器在区间[t2j,t2j+1)内工作，V1(t)在区间[t2j,t2j+1)内被激活；执行器在区间[t2j+1,t2j+2]内失效，V2(t)在区间[t2j+1,t2j+2)内被激活，j=1,2,…

(17)

并且由(11)知，V1(t)≤μV2(t),V2(t)≤μV1(t),

当t∈[t2j,t2j+1)时，V(t)≤eα(t-t2k)V(t2k)

≤μeα(t-t2k)V(t2k-)

≤μeα(t-t2k)e-β(t2k-t2k-1)V(t2k-1)

≤…

≤μNσ(0,t)eα(t-Tu(t))e-βTu(t)V(0)

(18)

当t∈[t2j+1,t2j+2)时，类似地有

V(t)≤μNσ(0,t)eα(t-Tu(t))e-βTu(t)V(0)

(19)

因此，对于任意的

由(16),(17)知t∈[t2k,t2k+2)

V(t)≤μNσ(0,t)eα(t-Tu(t))e-βTu(t)V(0)

(20)

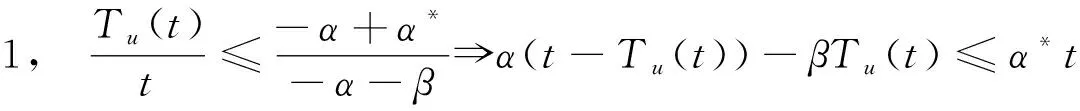
(21)

由(16),(17)得

V(t)≤μNσ(0,Tf)ea*TfV(0)

(22)

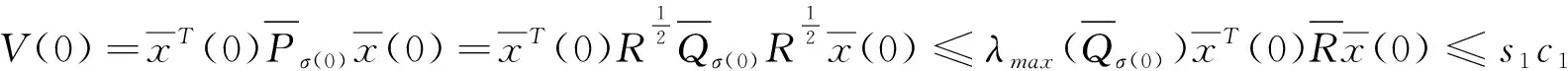
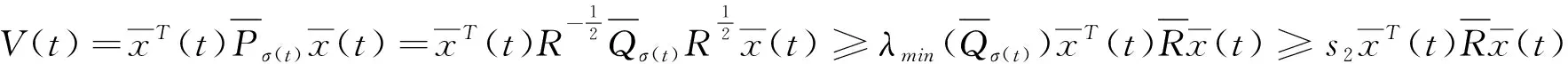
(23)

3 输出跟踪控制其设计

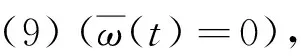
(24)

通过求解矩阵不等式即可得到控制增益，那么存在形式为(6)的状态反馈控制器，使得增广的闭环系统(9)是有限时间稳定的。而且，形式为(6)的控制增益矩阵为

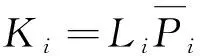
(25)

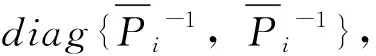
4 结 论

本文讨论了执行器失效的跟踪控制问题，给出等价的系统有限时间稳定的充分条件。利用李雅普诺夫函数和平均驻留时间机制方法分析了系统在有限的时间内的稳定性，并通过使用矩阵不等式方法给出了相应的控制器的设计方法。今后还将进一步考虑不确定的跟踪控制问题。