基于POMDP框架的集群无人机侦察任务可靠性建模

白桦，孙旭朋，黄文铮，阳辉

（北京圣涛平试验工程技术研究院有限责任公司，北京 100089）

引言

无人机智能化程度高、造价相对低廉，但在实际应用中也暴露出严重的安全隐患。在受到热、电、温循、振动等环境应力的影响下，无人机的失效率有可能升高；无人机的维护水平也制约每次任务能够投入的机器的架次。对于某型号无人机，其平均一般故障间隔时间为500 h，平均严重故障间隔时间为1 300 h，故障检测率为93 %[1]。2008年以来的无人机实际飞行公开数据显示，常用国外无人机机型和国内投入运行机型的故障间隔时间在9.1～55.1 h之间，可用度40～98 %[2]。无人机飞行风险可以总结为: 高危害性、不可控性和预测难度大[3]，其中不可控性是对于视距外的故障，地面人员无法针对无人机故障妥善处理。在现代控制方法支撑下，无人机向集群化方向发展，可以实现更多的任务。由于集群无人机的任务变化和功能时变性，给建立集群无人机可靠性与任务成功之间的关系模型带来了挑战。

POMDP是具有有限分立状态和有限行动选择的不可全知Markov系统在取得状态和行动对应回报下的决策问题[4]。POMDP框架可以应用于无人机对抗[5]、无线网络协议[6]、对话系统[7]等应用描述。POMDP的不确定性使得求解依赖于历史，占据庞大的数据空间。使过程期望回报最大的行动序列，称为最优策略。然而传统的POMDP值迭代算法需要在整个信念空间上更新值函数[4]，这种精确解法的时间和空间复杂度极高，只能解决小规模的POMDP问题。基于点的值迭代算法[8]只在少量信念状态上更新值函数，计算效率有所提高。论文[9]提出了一种紧凑的信念状态表示法，对于求解大规模POMDP问题具有良好性能。

本文将在POMDP框架下，考虑集群无人机可靠性对于任务的影响，对集群无人机侦察任务进行建模，通过仿真计算，构建包括战备完好率和单机失效率在内的可靠性指标与侦查任务实现效能的定量关系模型。

1 集群无人机POMDP控制方法

1.1 POMPD框架

POMDP模型用于描述具有隐藏的系统状态且行为效果是不确定的Markov过程。 POMDP模型用六元组{S,A,T,Ω,R,O}表示，其中S是系统所有状态的非空集合，部分状态是不能直接观察到的；A表示行动的有限集合；T表示状态转移函数，用表示观察点在状态S上对应行动A后转移到状态s′的概率；R是回报函数，R(s,a)表示观察点在状态s上对应行动a可提供的回报；O表示观察点被观察到的状态的有限集合；Ω 表示观察函数，用表示观察点对应行动a转移到状态s′后被观察到状态o的概率。

1.2 信念表示

信念状态是系统历史的充分统计量，由状态集合S上的概率分布组成的维向量。一种紧凑的信念状态表示法[9]假定系统的所有Markov过程均独立进行，认为此时可能存在一种维数随独立的系统点个数线性增长的信念表示。对于离散时间t组成的状态历史h，定义条件概率Ψ(t)：

其中(t)为系统点1置于状态的概率。而对于 任意h，可以证明观察到的条件概率分布Ψ(h)为系统点条件概率分布B(h)的一种等价表示[5]。从而系统点彼此独立时，紧凑的信念状态表示法可以使得POMDP状态空间随系统点数量仅线性增长。

1.3 状态更新

对于当前不可观察的系统点n，条件概率会按照Markov矩阵P更新。对于当前可观察的系统点n，系统点状态具有确定值，条件概率wn将会置于对应有限观察状态k的单位向量表示观察值为表示不可观察的部分。

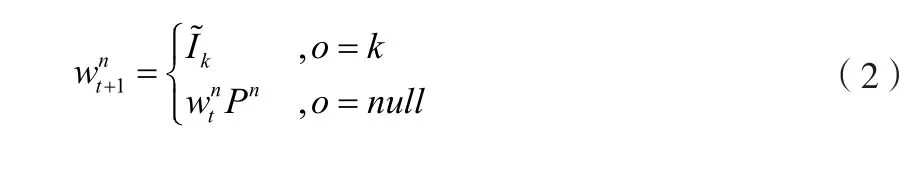
2 仿真计算条件设置

本文考虑的场景是：集群无人机在不确定环境下侦察，例如山火现场。集群无人机根据对环境的部分观察，自主规划获取最大侦察信息的路径，即寻找最大期望回报的行动组合。

地形被考虑成一系列系统点，每个点的环境信息在有限状态间的转换具有单调矩阵的属性。我们可以基于Markov单调矩阵特性，“预测”当前不可观察点的信念状态[9]。

每个系统点可以提供侦察回报，但同时具有对无人机的伤害能力。本文对每个系统点同时具有提供信息和给予伤害的属性，选取单调Markov矩阵进行描述，分别称为信息模型I和威胁模型R。本文把侦察信息和侦察威胁分为4种类型，分别具有5种信息状态和5种威胁状态。本文采用的复杂侦察地形图如图1。

图1 无人机侦察任务信息值地形图和威胁值地形图

格点代表侦察对象，连线代表可飞行路径。格点颜色区分不同的对象，格点对应属性变化规律为Markov矩阵～，～为信念向量。4种Markov矩阵及对应信念向量如下所示：

各状态对应回报值为：

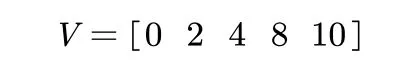
回报值是基于侦察信息状态oI和侦察威胁状态oR的回报值的组合函数。某时刻的侦察回报为：

式中：

本文用蒙特卡洛算法求解侦察回报，并设定集群无人机不在同一时刻巡逻同一系统点。同时减少无人机在侦察一个系统点后，下一个时间步时对其进行重复侦察的可能。具体为：当前时刻被侦察到的点，将在下一时刻按照单调Markov矩阵～首列的概率进行衍变，即有更大概率回报值取序列中的最小值。

3 仿真计算结果分析

3.1 路径搜索深度的影响

通过以上POMDP框架和信念表示求解本文设定地形。考虑每次决策都进行多步搜索，集群无人机依次考虑单机最大回报值路径，排次在后的无人机不到访同一时间步已有无人机侦察的系统点。假设无人机的续航时间为10 h，飞行速度为每0.01 h经过相邻系统点。集群无人机的初始位置为随机分布。仿真20架次无人机在不同路径搜索深度下的侦察回报，搜索深度从1到7步，每个状态的蒙特卡洛事例数100次。结果如图2所示。

可见，平均总回报值在4步搜索深度之后稳定，并基本达到饱和。为提高仿真计算效率，搜索深度将固定在4步。

3.2 无人机数量的影响

仿真计算5～25架无人机同时执行同一地形侦察任务的总回报值（图3），在集群无人机数量达到17时，回报值达到最大。曲线先增后减的走向是由于不同无人机探测同一地点时，信息值不重复计算，而威胁值是累加的，回报值因同时更多架次无人机受到伤害而减小。

3.3 可靠性指标的影响

假设战备完好率以及单架无人机的失效率为常数。本文建立无人机数量N取值范围在10～18架，战备完好率κ在60～100 %，单机失效率λ在1× 10-4- 5× 10-2h-1范围内的集群无人机侦察任务可靠性研究，定量分析侦察回报的影响因素。各条件蒙特卡洛仿真事例数均为400。

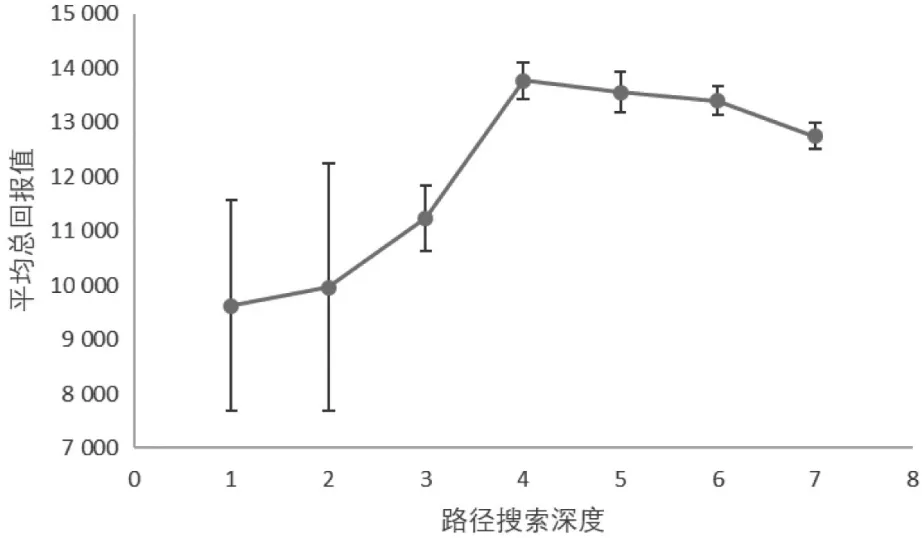
图2 20架无人机搜索深度与平均回报值标准差

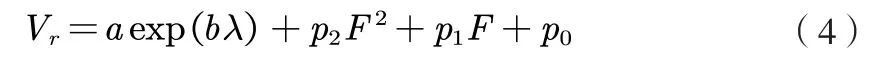
曲面是按曲面（4）对侦察回报值的拟合。用颜色区分任务架次的条件。

表达式（4）对出动架次的影响用二次多项式描述，对失效率影响采用指数形式。从图4可以看到，回报拟合曲面与仿真结果吻合，最大偏差在5 %以内，拟合结果见表1。

图5～6给出拟合回报值对出动架次和失效率的偏差分布。即在特定形和合理的战备完好率、失效率范围内，（4）在预测不同架次和失效率的侦察回报上表现稳定，可以有效评估架次和失效率变化对侦察回报的影响。

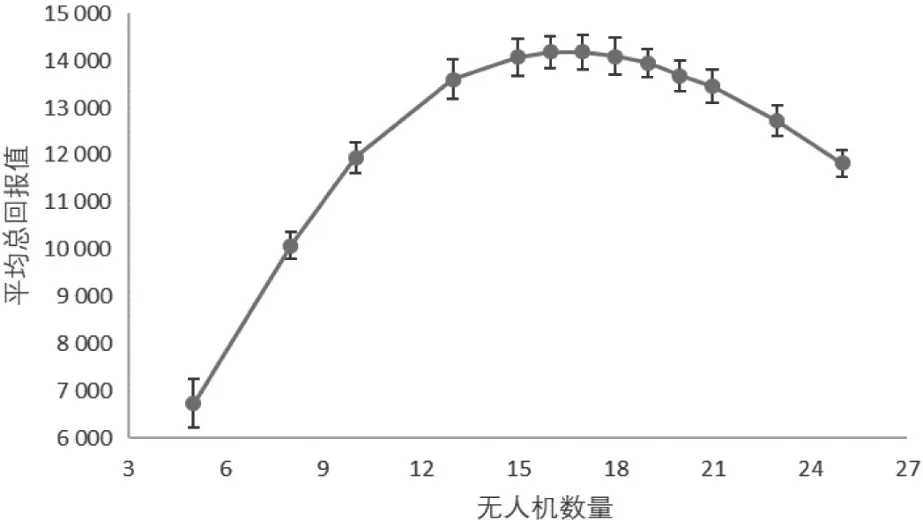
图3 无人机数量与平均回报值标准差

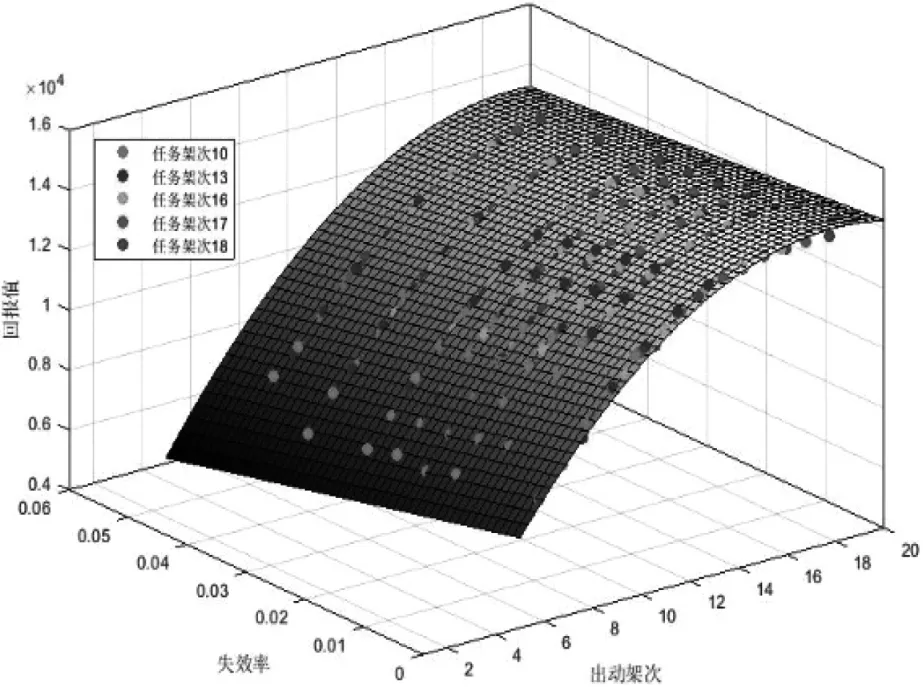
图4 无人机出动架次和失效率组合条件下侦察任务回报值

4 结论

本文对在给定的任务设定下，基于POMDP框架和蒙特卡洛仿真计算方法，对集群无人机侦察任务进行了仿真计算，给出了在有限探索深度下集群无人机自主决策的行动序列，建立了集群无人机总数、单机失效率、战备完好率与任务回报值时间的定量关系模型。该方法可为集群无人机侦查任务的可靠性指标的制定提供定量分析工具。

表1 拟合参数值

图5 不同出动架次下回报值预测误差分布

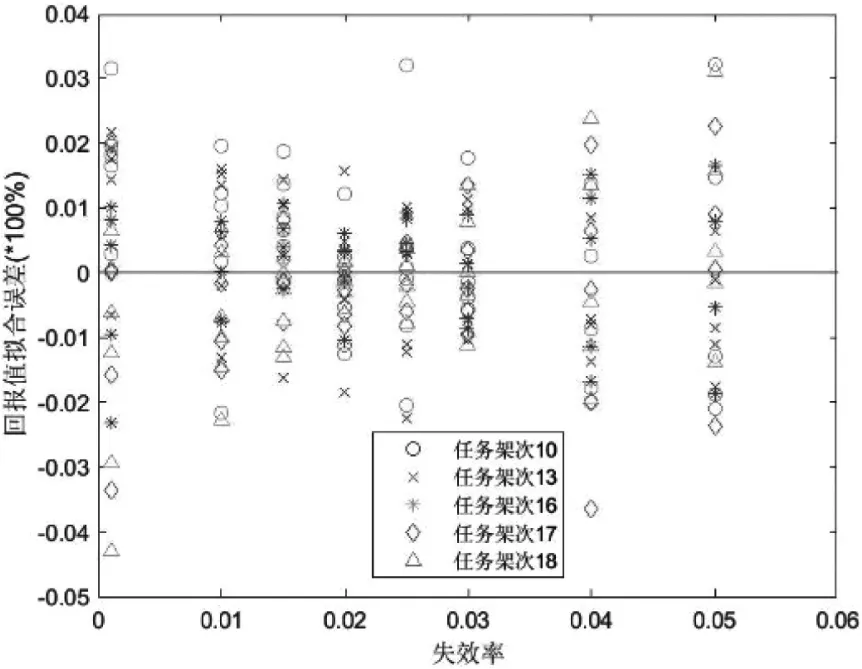
图6 不同失效率下回报值预测误差分布