二维移动网格矢通量分裂法

李彬彬，郑素佩，王 令

(长安大学 理学院 陕西 西安 710064)

0 引言

在对非线性双曲守恒律方程进行数值求解时，即使在初始条件充分光滑的条件下，在某一时刻解也可能存在激波或稀疏波等间断，寻找满足物理意义的唯一弱解成为研究双曲守恒律方程的关键。文献[1-3]对矢通量分裂法进行了研究，并给出了通量如何选择的建议。数值结果的好坏不仅与格式有关，还与网格的分布相关。根据解的性质对网格节点进行合理的分布，对高效、精确地计算非线性双曲守恒律方程具有极其重要的作用，为此文献[4]首次提出了自适应技术。目前，引起学者广泛关注的是拉格朗日法细化后的移动网格法。移动网格法将方程的求解和网格的移动作为两个完全独立的部分，该算法具有易于推广的特点。自20世纪80年代以来，文献[5]开始利用自适应移动网格法提高分辨率。已有的大多数研究都是采用移动网格法来求解一维的动力学方程[6]。2003年，文献[7]提出了求解多维双曲守恒律方程的移动网格算法，能有效地解决激波间断问题。到目前为止，将移动网格法与矢通量格式进行耦合的研究还很少。因此，本文将移动网格与矢通量分裂格式进行耦合来求解二维欧拉方程组，通过构造新的监控函数以及物理量守恒映射提高移动网格的通用性，既保证求解过程中网格合理分布和提高间断处的分辨率，也保证原格式的高精度特点。此外，二维欧拉方程组的数值算例模拟结果表明了新算法具有良好的间断捕捉能力和高分辨率。

1 控制方程

考虑如下二维守恒型欧拉方程[8]：

(1)

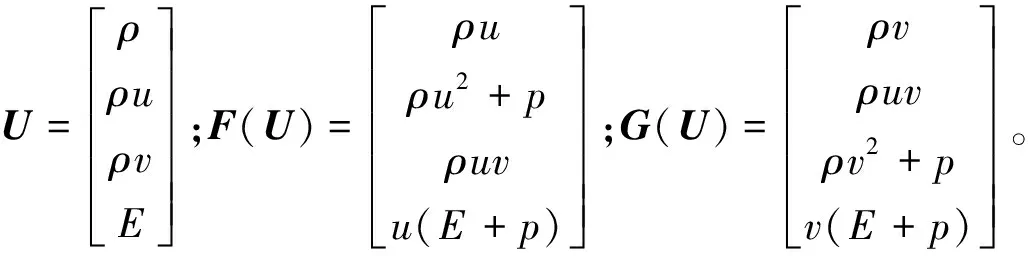
记H=[F,G]·n，则式(1)可简写为

(2)

时间方向上采用文献[9]提出的TVD型龙格-库塔方法进行离散，

式中：L是空间离散算子。

2 网格剖分

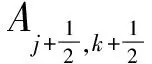
(3)

边界上函数积分为

(4)

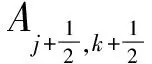
(5)

将式(4)和式(5)代入式(3)，可得

(6)

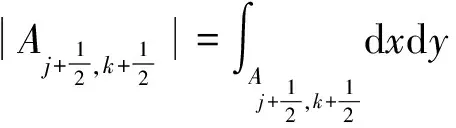
由中值定理，可得式(6)的近似值为

(7)

式中：Δlk是Ik(k=1,…,4)的长度；Hk是Ik(k=1,…,4)中点处的函数值。

3 基于变分原理的移动网格法

对文献[7]中的监测函数和物理量守恒映射方法进行改进，以提高移动网格法的通用性。

3.1 二维移动网格法

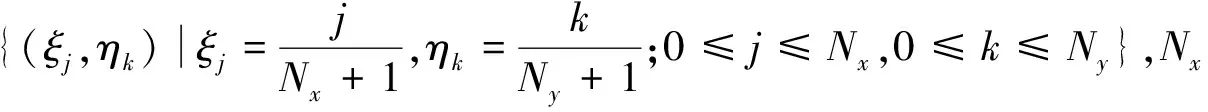
z=z(ζ),ζ∈Ωc。

(8)

在变分法中，网格映射使得在计算区域如下函数达到最小值，具体函数表示式为

(9)

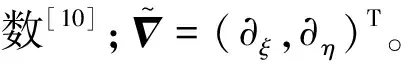
令G=ωI，对应的欧拉-拉格朗日方程为

(ωxξ)ξ+(ωxη)η=0,ζ∈Ωc,

(10)

用中心差分格式离散式(10)，可得

(11)

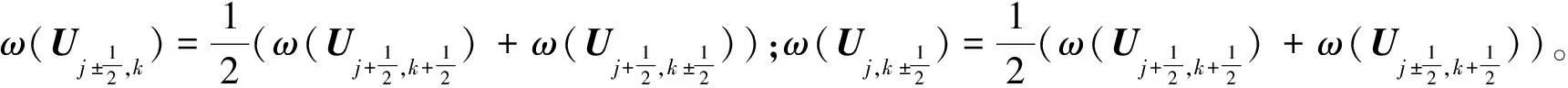
采用高斯赛德尔迭代法求方程(11)的近似解，可得

(12)

为避免数值解产生较大的误差，可用低通滤波器对监控函数进行光滑化[11]，

(13)

3.2 基于迎风格式的物理量守恒映射

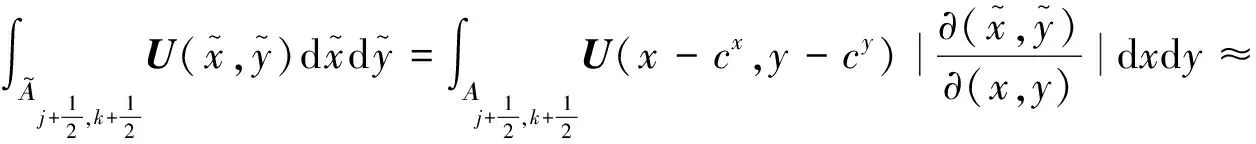
(14)

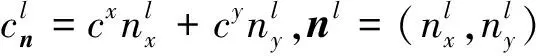
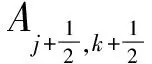
(15)

(16)

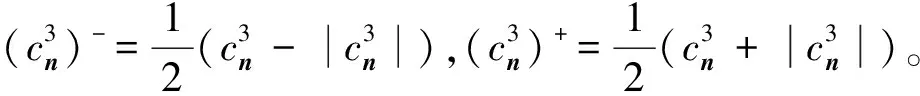
为了提高间断处的分辨率，构造二阶精度的迎风型物理量守恒映射，

(17)

(18)

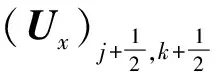
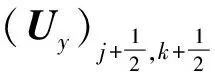
(19)

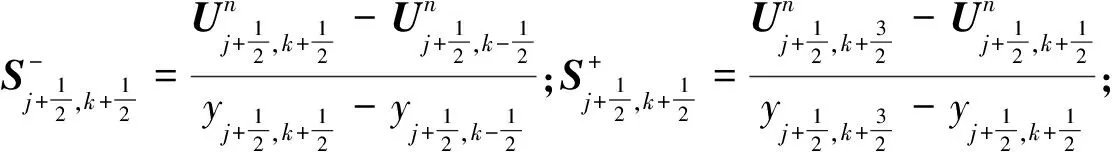
(20)

3.3 基于非结构网格的矢通量分裂法

(21)

式中：zci为Ik界面的中点坐标。旋转不变性的数值通量Hk为

(22)

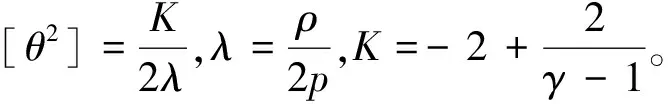
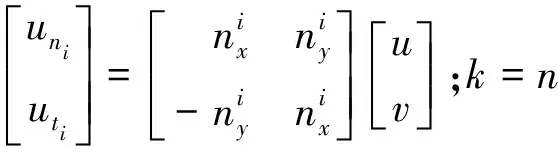
4 数值算例

算例1双马赫反射问题

计算区域为[0,4]×[0,1]，在其底部有一个始于x=1/6的墙。在计算开始时刻，一个马赫数为10的右激波通过点(1/6,0)，并与x轴成60°夹角。则初始解为

其中左状态UL、右状态UR和激波的位置h分别为

左边界和右边界分别设为入流边界和出流边界，需要根据激波运动对上边界进行分类讨论，在x=1/6时对下边界采用无穿透绝热条件。计算网格为160×40，计算时间推进到t=0.2。在数值模拟中，画图区域仅截取[0,3.1]×[0,1.0]。图1为双马赫反射问题的移动网格演化图和密度图。可以看出，移动网格集中分布在点(2.7,0.41)和(2.6,0)附近；网格演化图的间断区域分布较多网格节点，过渡带明显变窄，具有较高的分辨率。

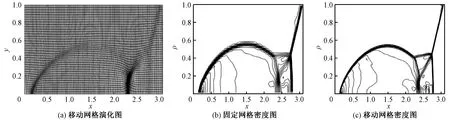
图1 双马赫反射问题的移动网格演化图和密度图Figure 1 Moving grid evolution map and density map of double Mach reflection problem

算例2二维欧拉方程的黎曼问题1

初值为

其解包含两个双马赫反射，计算区域为[0,1]×[0,1]，计算网格为100×100，两侧的边界条件使用出流边界条件，计算时间为t=0.25。图2为黎曼问题1的移动网格演化图和密度图。可以看出，激波两交点(0.92,0.3)和(0.3,0.92)附近网格进行了加密处理；随着网格节点自适应加密，弧形激波过渡区明显变窄。

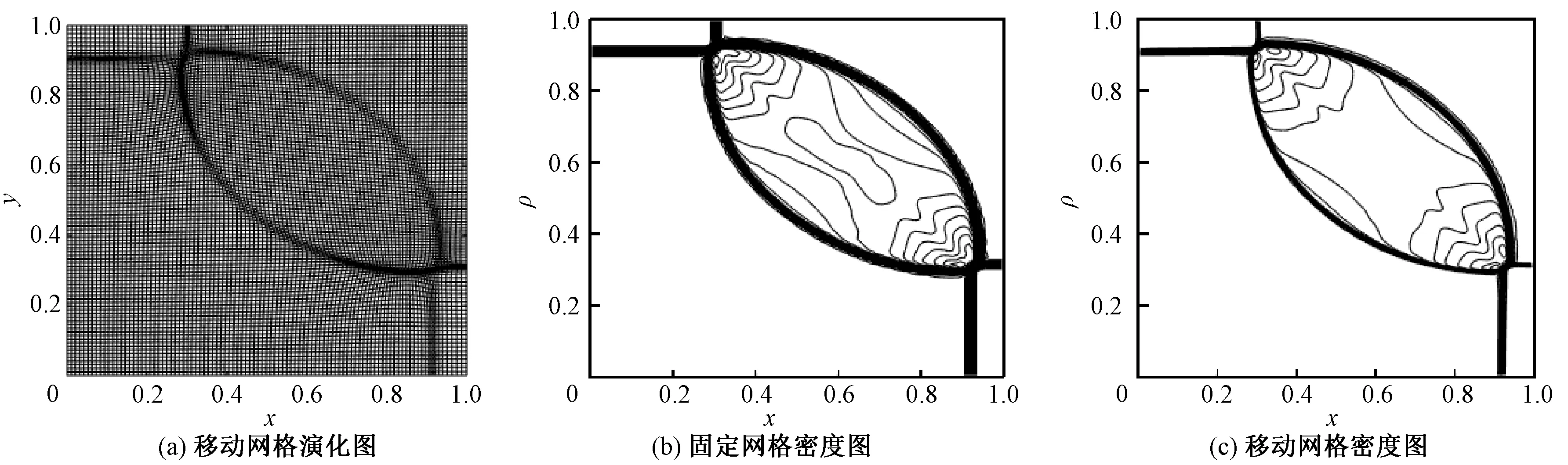
图2 黎曼问题1的移动网格演化图和密度图Figure 2 Moving grid evolution map and density map of Riemann problem 1

算例3二维欧拉方程的黎曼问题2

初值为

计算区域为[0,1]×[0,1]，计算网格为100×100，两侧的边界条件使用出流边界条件，计算时间为t=0.25。图3为黎曼问题2的移动网格演化图和密度图。可以看出，弧形激波和马赫反射等间断区域分布较多的网格节点；移动网格间断处进行了自适应加密，间断处过渡带相对于固定网格更窄，能更准确地捕捉间断。

图3 黎曼问题2的移动网格演化图和密度图Figure 3 Moving grid evolution map and density map of Riemann problem 2

5 结语

本文将移动网格算法与高分辨率矢通量分裂格式耦合，得到了一种求解二维双曲守恒律方程的移动网格矢通量分裂格式法。三个数值算例的模拟结果表明，新算法能有效地捕捉间断和提高间断处的分辨率，且易于编程和向高维问题推广。