多粒度近似空间的模糊粗糙集模型
2020-11-18秦克云
胡 谦,秦克云
(1.西南交通大学 信息科学与技术学院 四川 成都 611756;2.西南交通大学 数学学院 四川 成都 611756)
0 引言
1982年波兰学者Pawlak提出了粗糙集理论[1], 它是一种处理不完备不精确数据的有效数学工具[2]。粗糙集不需要给出额外信息, 算法简单, 实用性强。因此它已经成为一种重要的智能信息处理方法, 并广泛应用在机器学习、模式识别、管理等领域[3-5]。1965年Zadeh教授提出了模糊集的概念[6], 随后模糊数学在理论和应用方面都得到了飞速发展。经典的粗糙集理论所处理的对象属性为离散值。而在现实生活中, 连续属性值和模糊属性值是普遍存在的。因此把模糊集与粗糙集相结合研究实际问题中的不确定性成为粗糙集理论推广的主要方向之一[7-9]。
文献[10]将单粒度粗糙集模型拓展到多粒度情形, 用一簇属性子集的集合来代替一个属性集来对论域进行分类, 即由属性子集的集合确定论域的层次划分, 构造出多粒度空间。近年来多粒度粗糙集理论成为一个研究热点[11-20]。然而原始的多粒度模型上、下近似定义中, 悲观下近似要求对象在所有粒度下的等价类都要包含在目标对象集中, 而乐观下近似要求对象在有一个粒度下等价类包含在目标对象集中。悲观下近似的条件过于严苛,而乐观下近似的条件过于松弛, 同时在广义多粒度粗糙集模型中无法区分不同粒度的重要性。针对这两个问题, 为使多粒度模型更适用于实际数据, 提高模型的适用性, 更好地考虑不同粒度重要性, 本文提出了一种处理多粒度数据的方法, 该方法可以从多粒度近似空间中得到基于对象的不同粒度的重要度, 进而构建论域中对象之间的相似度, 然后基于对象的相似度定义一对模糊上、下近似;最后讨论了在多粒度近似空间中用该方法得到的上、下近似与其他形式的多粒度上、下近似之间的关系。
1 预备知识
在本节中, 我们主要介绍经典粗糙集、模糊粗糙集模型与多粒度粗糙集模型的定义及性质。
1.1 Pawlak粗糙集模型及其推广模型
定义1[1]设I=(U,A,F)是一个信息系统, 其中:U={x1,x2,…,xn}称作论域;A={a1,a2,…,am}是非空属性集合;F={fa|a∈A}为关系集,fa:U→Va,Va为属性a的值域。由A可以得到U上的一个二元等价关系R, 即∀x,y∈U,(x,y)∈R当且仅当fa(x)=fa(y),称(U,R)为一个Pawlak近似空间。对于任意X⊆U,X关于(U,R)的上、下近似分别定义为
其中:[x]R={y∈U|(x,y)∈R}为x关于R的等价类。
为扩展粗糙集的应用范围, 人们提出了多种形式的粗糙集推广模型。
定义2[21]设U为论域, 若R是U上的一个二元关系, 即R⊆U×U, 则称(U,R)为一个广义近似空间。对于任意X⊆U,X关于(U,R)的上、下近似分别定义为
其中:R(x)={y∈U|(x,y)∈R}为x关于R的右邻域。
经典的粗糙集一般处理的是离散型数据, 然而在实际生活中存在着大量连续性数据, 此时经典的粗糙集模型不再适用。因此人们将粗糙集与模糊集结合提出了模糊粗糙集模型。
1.2 多粒度粗糙集模型
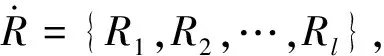


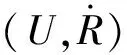

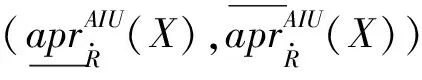
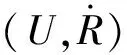

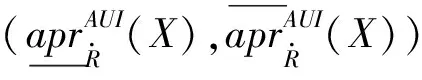
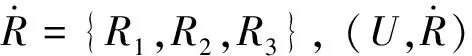
U/R1={{x1},{x2,x3,x4},{x5,x6}},U/R2={{x1,x2,x3},{x4,x5},{x6}},
U/R3={{x1,x2,x3,x4},{x5,x6}},U/∩R={{x1},{x2},{x3},{x4},{x5},{x6}}。

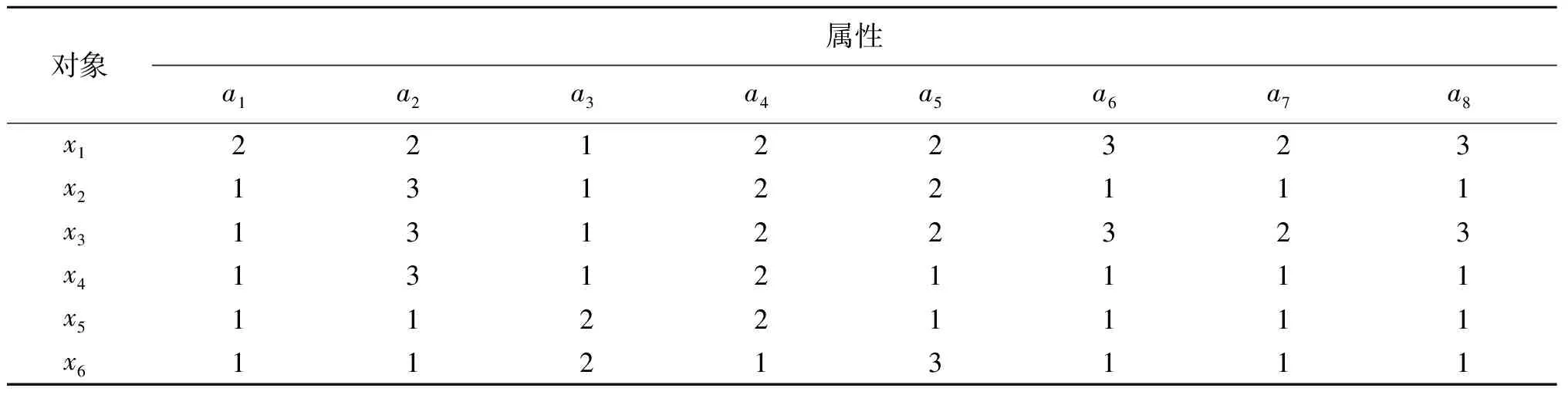
表1 信息系统I=(U,A,F)Table 1 The information system I=(U,A,F)
悲观多粒度粗糙集与乐观多粒度粗糙集均不能由等价关系诱导[14], 下面的引理说明悲观多粒度粗糙集可以由一个自反、对称关系诱导。
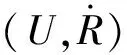

2 基于粒度重要度的多粒度近似算子
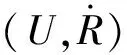
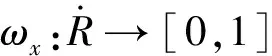
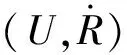
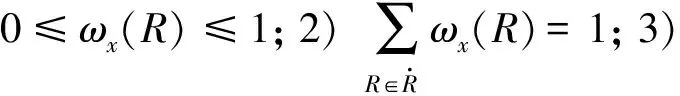
证明1)由定义可知0≤ωx(R)≤1显然成立。
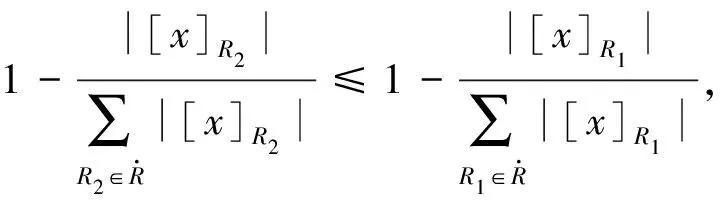
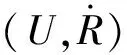
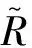
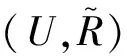
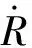
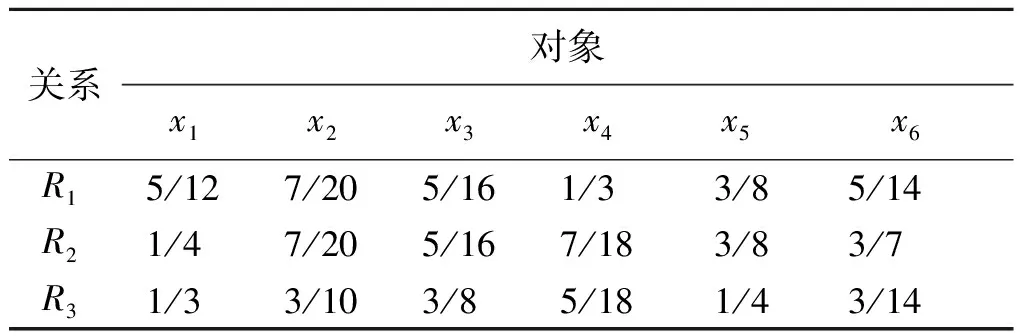
表2 等价关系重要度Table 2 The significance of equivalence relation
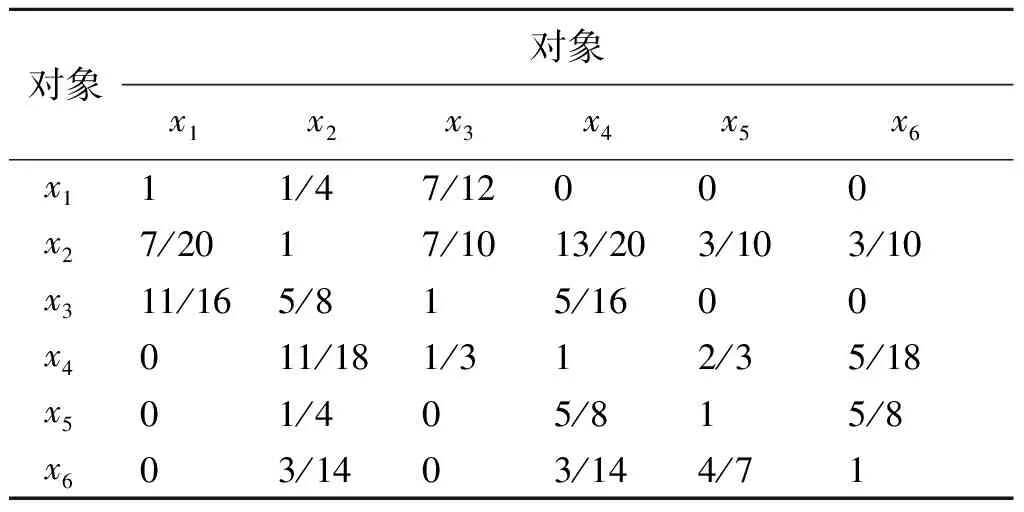
表3 对象相似度Table 3 The similarity degree between objects
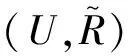

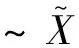
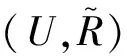
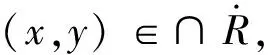
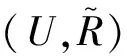
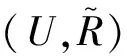
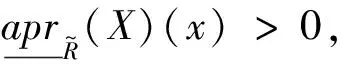
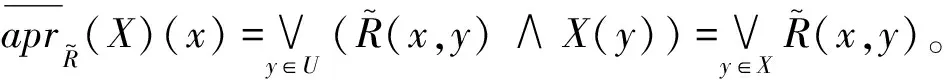
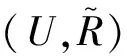
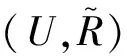
证明由定理3显然可证。
3 结论
本文提出了一种处理数据的方法, 该方法可以从多粒度近似空间中得到基于对象的不同粒度的重要度, 进而构建对象之间的相似度, 然后基于对象的相似度给出模糊上、下近似的定义, 最后讨论了多粒度近似空间中用该方法得到的上、下近似与其他形式的多粒度上、下近似之间的关系。在多源数据或多尺度信息系统下,利用该方法进行信息融合以及如何在实际问题中进行应用是下一步需要解决的问题。
