PCA 降维技术在弯辊力预设定中的研究与应用①
2020-11-18卜赫男叶鹏飞闫注文韩子延
卜赫男, 叶鹏飞, 闫注文, 韩子延
(1.江苏科技大学 机械工程学院,江苏 镇江212003; 2.南京工程学院 智能装备产业技术研究院,江苏 南京211167)
冷连轧板带材是钢材的关键品种之一,板形是衡量冷轧带钢产品质量的主要指标和决定其市场竞争力的重要因素[1]。 板形预设定控制系统是板形控制系统的重要组成部分,在热轧原料带头被轧辊咬入的瞬间直至实现稳定轧制的过程中,板形反馈控制系统无法投入,此时需要采用预先设定的板形调节机构调节量来控制带钢在此期间的板形。 同时,当板形反馈控制系统投入运行时,该调节量又会成为反馈控制的起点与初值。 由此可见,板形预设定控制的精度影响到每一卷带钢的成材率,其设定正确与否对反馈控制作用下板形达到目标值的收敛速度和精度至关重要[2]。
液压弯辊是板形控制的重要手段,实际生产中,可以通过改变弯辊力实现板形在线控制[3]。 针对弯辊力预设定模型,国内外已有相关研究成果[4-6]。 现代化的冷连轧生产线配备有大量传感器,实时采集的信息数据以GB 为单位存储在服务器中,如何科学、高效地处理轧制过程工艺参数,提高控制效率,仍是冷轧生产单位亟待解决的问题[7]。 降维是钢铁大数据建模和计算的解决思路之一,降维处理在减少数据的同时能够保证尽可能少的数据信息丢失,为后续数据分析打下良好基础。 本文采用PCA 降维技术处理轧制过程数据,进而构建弯辊力预设定新形态模型,实现模型收敛速度和计算效率的提升。
1 弯辊力预设定模型
某冷轧厂1 450 mm 酸洗冷连轧生产线的主要原料为普通低碳钢、优质低碳钢等,通过冷连轧机连续轧制为CQ、DQ、DDQ、EDDQ、SEDDQ 等钢种的带钢,最终获得所需厚度和表面粗糙度的各类规格冷轧卷。 该生产线能够批量化稳定生产0.17 mm 薄带钢,最高轧制速度可达1 350 m/min。
该生产线过程自动化控制系统目前采用遗传算法优化的BP 神经网络实现弯辊力的预报。 BP 神经网络采用三层拓扑结构,通过信号的前向传递(输入层→隐含层→输出层)及误差的反向传递(输出层→隐含层→输入层)对神经元间的连接权值和阈值进行修正,直至满足终止条件,完成弯辊力的预设定[8]。 充分考虑弯辊力影响因素,选取轧制力、带钢入口厚度、出口厚度、带钢材质、工作辊凸度、中间辊凸度、带钢宽度、带钢凸度、工作辊直径和中间辊直径10 个特征作为神经网络的输入,工作辊弯辊力和中间辊弯辊力作为神经网络的输出,网络结构如图1 所示。
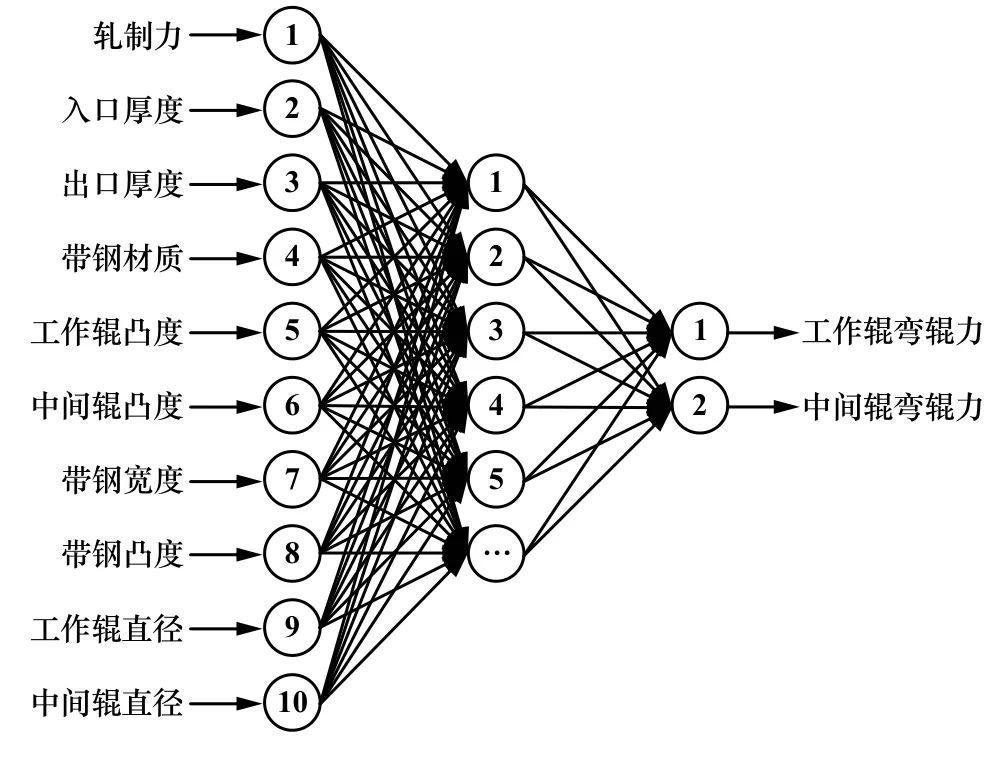
图1 神经网络结构
在神经网络训练过程中,由于初始权值和阈值的随机给定,前向传递时很容易陷入局部最小值,为了提高获得全局最优解的概率,采用遗传算法(GA)对网络初始参数进行优化,计算流程如图2 所示。

图2 GA⁃BP 神经网络计算流程
GA⁃BP 神经网络能够满足预设定阶段板形控制精度的要求,但仍存在训练时间长、收敛速度慢等问题,尤其数据维度的提升将使网络性能迅速下降。 为进一步提高神经网络计算效率,本文通过数据降维技术将大量高维数据投射到低维空间,并将携带了大量数据信息的低维数据作为神经网络的输入,以此实现GA⁃BP 神经网络预测性能的提升。
2 PCA 降维技术的原理与应用
2.1 PCA 原理
主成分分析(Principal Component Analysis,PCA)是采用降维的思想,在力求数据信息丢失很少的前提下,对高维变量空间进行重新组合,把多个指标利用正交旋转转化为少数几个综合指标的多元统计分析方法[9]。 在PCA 中,数据从原来的坐标系转换到了新的坐标系,第一个新坐标轴选择的是原始数据中方差最大的方向,第二个新坐标轴的选择与第一个坐标轴正交且具有最大方差的方向,重复以上过程,重复次数为原始特征数。 执行以上操作后,大部分方差都包含在最前面的几个新坐标轴中,余下的坐标轴则可以被忽略[10]。
采用该方法将错综复杂的变量转化生成的综合指标变为主成分,其中每个主成分都是原始变量的线性组合,以此实现数据的降维处理[11]。
PCA 的原理描述如下:
用涉及事物的p个指标的随机向量X=(X1,X2,X3,…,XP)′来做线性组合,则:

若上述方程中的系数uij满足以下3 个条件,则该系数值就分别称为Y1,Y2,…,YP的第一,第二,…,第P个主成分,选取累积贡献率最大的主成分个数作为最终的输出结果,即:
1)u1i2+u2i2+…+upi2=1 (i=1,2,3,…,p);
2)Yi与Yj不相关(i≠j;i,j=1,2,…,p);
3)Y1是X1,X2,…,Xp满足式(1)的线性组合中方差最大的;Y2是与Y1不相关的X1,X2,…,Xp的所有线性组合中方差最大的;…;YP是与Y1,Y2,…,Yp都不相关的X1,X2,…,Xp的所有线性组合中方差最大的。
2.2 PCA 计算流程
PCA 的求解遵循以下步骤:
1) 原始数据标准化。 采集p维随机向量,构造样本阵。 为消除变量之间的量纲影响并提高模型计算精度,对变量数据进行标准化处理。 采用Z⁃Score 标准化方法基于原始数据的均值和标准差进行数据的标准化,经过处理的数据符合标准正态分布,其均值为0,标准差为1。 转换函数如式(2)所示,标准化处理后计算各变量之间的协方差矩阵。

式中为原始数据的均值;σ为原始数据的标准差。
2) 求协方差矩阵特征值及特征向量。 计算协方差矩阵的特征向量为λ1≥λ2≥…≥λp,相应的单位特征向量为U1,U2,…,Up,其中转换矩阵A=U′,即A的第i行就是协方差矩阵的第i个特征根对应的单位特征向量ui,且第i个主成分Yi的方差就等于协方差矩阵的第i个特征根λi。
3) 计算方差贡献率及累积贡献率。 第k个主成分Yk的方差贡献率如式(3)所示:

若取m(m<p)个主成分,则主成分Y1,Y2,…,Ym的累积贡献率如式(4)所示:

4) 选取主成分个数。 主成分个数的选取一般取决于累积方差贡献率。 通常取m个主成分使得方差的累积贡献率达到90%以上,则对应的前m个主成分的样本信息量包含p个原始变量所能提供的绝大部分信息。
2.3 PCA 应用
选取该1 450 mm 冷连轧生产线多卷带钢轧制数据共2 000 条作为数据样本,其中1 500 条作为训练集,500 条作为测试集,对训练集数据进行PCA 降维操作,在数据标准化处理后,采用前述公式计算特征值及方差贡献率,如表1 所示。

表1 特征值及方差贡献率
由表1 可知,前3 个主成分特征值的累积方差贡献率达到90%,因此选择前3 个成分代替原变量。 采用标准化的正交旋转法得到各个因子对不同主成分的因子载荷,得到的成分矩阵如表2 所示。

表2 成分矩阵
采用PCA 降维技术获得的主成分值为:

式中X1、X2、…、X10分别代表轧制力、出口厚度、工作辊凸度、带钢材质、工作辊直径、中间辊凸度、带钢宽度、带钢凸度、入口厚度和中间辊直径。
3 现场测试与结果分析
冷轧带钢板形良好的条件为实际板形曲线尽可能接近于目标板形曲线,即各个测量段上的板形偏差均方差值最小[12],如式(6)所示:

式中f为板形偏差值;n为测量段总个数(现场测试带钢n=20);i为测量段编号;Ftari为第i个测量段的板形目标值;Fmeai为第i个测量段的板形测量值。
将式(6)作为神经网络的适应度函数,神经网络的输出为5 个机架的工作辊及中间辊弯辊力值,因此以2 种模型构建的神经网络拓扑结构分别为10⁃20⁃10和3⁃20⁃10,即输入层节点数分别为10 和3,隐含层节点数为20,输出层节点数为10。 在训练集上对神经网络进行训练,然后在测试集上验证神经网络的性能,以均方误差计算预报值和实际值之间的偏差来评估模型预测性能,可得到GA⁃BP 神经网络在训练集的均方误差为0.98×10-4,在测试集的均方误差为1.57×10-4,PCA⁃GA⁃BP 神经网络在训练集的均方误差为1.12×10-4,在测试集的均方误差为1.63×10-4,2 种模型均满足预期精度要求,具有较强的泛化能力。
将本文提出的PCA⁃GA⁃BP 神经网络弯辊力预设定模型应用于1 450 mm 五机架冷连轧机组过程控制系统,随机选取一种带钢,分析其控制效果。 带钢相关参数为:钢种Q195;宽度1 250 mm;压下率87%;轧制策略为压下模式。 带钢主数据如表3 所示。 分别采用2 种模型计算的该带钢弯辊力预设定值如表4 所示。

表3 来料主数据
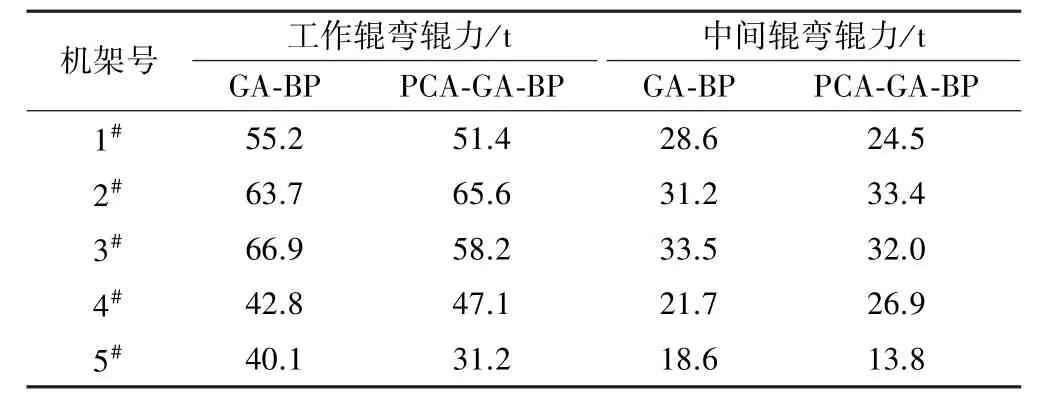
表4 弯辊力预设定值
其中,GA⁃BP 神经网络经过147 次迭代收敛于全局最优解0.996 564×10-3,耗时115 ms;PCA⁃GA⁃BP 神经网络经过61 次迭代收敛于全局最优解0.985 222×10-3,耗时42 ms,如图3 所示。
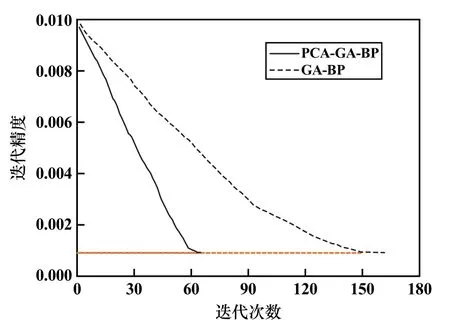
图3 迭代过程比较
图4 为板形闭环控制系统未投入阶段弯辊力预设定值作用下的带钢头部板形偏差对比图。 由图4 可以看出,GA⁃BP 神经网络作用下的带钢头部各测量段最大平均板形偏差为16.12 I,最小平均板形偏差为11.60 I,测量段总体平均板形偏差为12.61 I;PCA⁃GA⁃BP 神经网络作用下的带钢头部各测量段最大平均板形偏差为16.79 I,最小平均板形偏差为12.53 I,测量段总体平均板形偏差为13.47 I,均满足带钢头部板形控制精度要求。 但弯辊力预设定过程中,与GA⁃BP 模型相比,PCA⁃GA⁃BP 模型收敛于最优解时需要较少的迭代次数及较短的计算时间,大幅度提高了模型的计算效率。
4 结 论
1) 提出了一种基于PCA⁃GA⁃BP 神经网络的弯辊力预设定模型,通过PCA 将10 维输入数据降维至3个携带大量数据信息的主成分变量,并以此作为BP神经网络的输入,有效减少了各轧制数据之间的相关性,并简化了弯辊力预设定模型的结构及训练过程。
2) 基于现场实际数据对提出的模型进行训练及测试,结果显示,与原模型相比,新模型迭代速度快、计算效率高,同时能够保证弯辊力预设定值作用下的带钢头部板形精度。
3) 验证了PCA 数据降维技术在实际工程领域应用的可行性,对推动钢铁大数据与轧制过程相融合以及轧钢领域其他控制系统的建模与优化具有重要理论意义及实际应用价值。
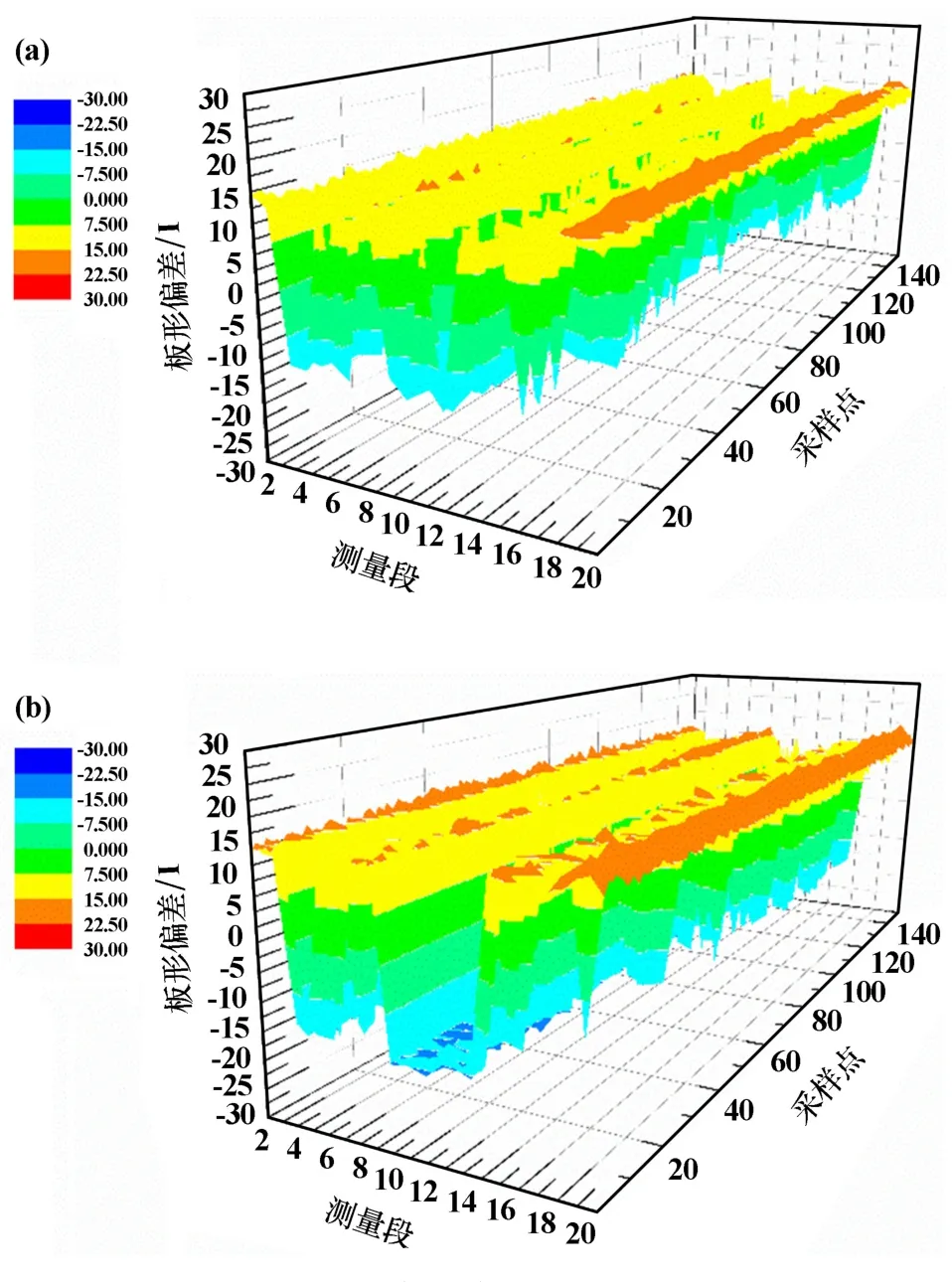
图4 板形偏差对比图
