基于多阶段递进识别的风电机组异常运行数据清洗方法

王一妹， 刘 辉， 宋 鹏， 胡泽春， 邓晓洋， 吴林林

（1.国网冀北电力有限公司 电力科学研究院， 北京 100045； 2.风光储并网运行技术国家电网公司重点实验室，北京 100045； 3.清华大学 电机系， 北京 100084）

0 引言

随着风电场建设的大型化， 风电场内海量数据的收集及处理问题日益突出[1]。 作为风电场单机信息管理的重要依据， 风电机组运行的数据采集与监视控制系统（SCADA）在风电场优化控制和发电功率预测等工程领域有着广泛应用。 SCADA数据的质量在很大程度上决定了风电场优化控制及功率预测的准确性， 进而影响风电场的经济效益[2]。 因此，研究能够有效提升SCADA 数据质量的风电机组运行数据清洗方法， 对于提高风电场运行维护的准确性和经济性具有重要意义[3]。

学者及工程人员针对风电机组的风速-功率（P-V）运行数据清洗开展了大量研究。Yan Jie[4]基于风电机组控制策略判断散点分布的上临界曲线剔除异常数据， 但判断过程须借助机组运行的桨距角信息。 Shen Xiaojun[5]利用变点分组法与四分位法结合的方式清洗异常数据， 但清洗过程存在数据点大量误删的情况。 娄建楼[6]采用最优组内方差法清洗风电机组的P-V 运行数据，但原始数据存在明显的正常与异常点分布，个例特性较强，应用的鲁棒性较差。 胡阳[7]利用置信等效边界法处理异常运行数据，但Copula 函数的差异性选取会导致计算边界对真实边界的覆盖偏差， 从而造成数据漏删或误删。

针对现有的风电机组运行数据清洗方法存在的需要额外信息辅助判断、数据误删量大、清洗后散点分布不光滑、鲁棒性差等问题，本文结合常见的异常数据类型， 提出了基于多阶段递进识别的风电机组运行数据清洗方法。 基于取自SCADA的风电机组P-V 数据，将异常运行数据划分为4类， 并针对不同类型的异常数据分别探索解决方案。 利用DBSCAN 聚类法、核密度估计法、截断法和斜率控制法分别建立异常数据识别模型， 用以识别离散分布的异常点、限功率点、0 功率的故障点以及1 功率的低风速点， 通过异常点剔除实现数据清洗，在保留数据完整性的基础上，提高了风电机组风速-功率运行数据的准确性。

1 风电机组运行数据

基于SCADA 中的风电机组实测P-V 数据，绘制机组标准化的实测P-V 散点图（图1）。由图1可知， 风电机组常见的异常运行数据大致可分为4 类，由下至上依次为①0 功率值堆积点、②恒功率限电点、 ③发电功率离群异常点和④1 功率值低风速点。

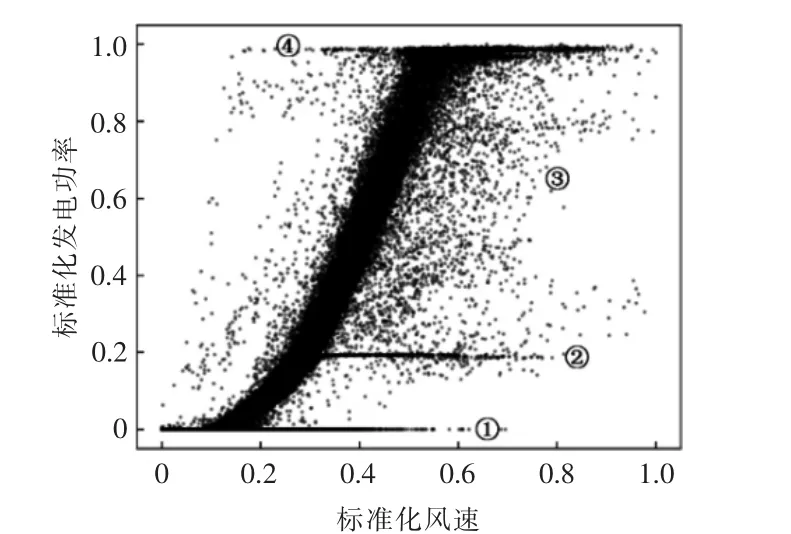
图1 风电机组实测P-V 散点图Fig.1 Measured P-V scatter for wind turbine

0 功率值堆积点常由风电机组故障、 计划外停电检修及通讯设备故障等原因产生； 恒功率限电堆积点多是因风电场跟踪调度计划的要求，而将场内的某些或全部机组控制在给定功率运行而产生；离群异常点常由极端天气、信号传播噪声等较为随机的因素导致；1 功率值低风速点多由通讯错误或传感器故障等非运行因素导致。 在实际运行中，①，③，④类异常数据的出现频率较高，②类异常数据则只针对限电机组。 在数据清洗过程中，4 类数据的处理顺序为③-①-④-②。

2 异常数据识别模型

本节针对③，①，④，②类异常数据的识别方法，依次进行原理解析。

2.1 基于DBSCAN 的密度聚类方法

密度聚类方法假设能够通过样本分布的紧密程度确定聚类结构[8]，并且将具有足够密度的区域划分为簇。 DBSCAN 是一种应用广泛的密度聚类方法[9]，利用邻域参数（Eps，MinPts）刻画样本分布的紧密程度，Eps 和MinPts 分别为半径和最小样本数目。基于邻域参数，DBSCAN 算法将数据点分为核心点、边界点和噪音点，噪音点就是数据清洗时须要识别的离群异常点。在已知邻域参数时，DBSCAN 算法的一般步骤如下：

（1）将数据集D 中的所有对象均标记为未处理状态；

（2）对数据集D 中的每个对象p 进行判断，如果p 已经被归入某个簇或被标记为噪声， 则结束判断，否则，继续执行步骤（3）；

（3）检查对象p 的Eps 邻域NEps（p），如果NEps（p）包含的对象数小于MinPts，则标记对象p为边界点或噪声点， 否则， 则标记对象p 为核心点，建立新簇C，并将p 邻域内的所有点加入C；

（4）对于NEps（p）中尚未被处理的对象q，检查 其Eps 邻 域NEps（q），若NEps（q）包 含 至 少MinPts 个对象，则将NEps（q）中未归入任何一个簇的对象加入C。

2.2 截断法

2.3 斜率控制法

当来流风速高于风电机组的切入风速时，机组的发电功率会随着风速的增加而增大直至达到满发（来流风速达到额定风速）。但在实际运行中，由于环境条件的变化以及机组控制策略等的影响， 机组达到满发功率的风速会略高于或低于设计的额定风速[10]。然而，显著低于额定风速的1 功率值散点，则是由通讯故障等原因造成的异常点，须予以剔除。

2.4 核密度估计方法

核密度估计（Kernel Density Estimation，KDE）是一种用于估计概率密度函数（Probability Density Function，PDF）的非参数检验方法[11]。 KDE 采用平滑的峰值（核）函数来拟合观察到的数据点，从而模拟真实的概率分布曲线。恒功率的限电堆积点经常覆盖较宽的风速范围，KDE 方法假设风电机组P-V 散点的PDF 服从正态分布， 而由于堆积型异常数据的存在， 此PDF 将呈现双峰或多峰分布。 对不同风速区间内功率散点的PDF曲线进行削峰处理，删除低峰密度曲线对应的异常点，使其由多峰变为单峰分布，完成限电堆积数据的清洗。

假设样本X 包含n 个独立同分布的样本点x1，x2，…，xn，其概率密度函数为f，KDE 将每个数据点的数据和带宽作为核函数的参数， 得到n 个核函数参数对， 经线性叠加后获得核密度的估计函数，经归一化后获得核密度的PDF。

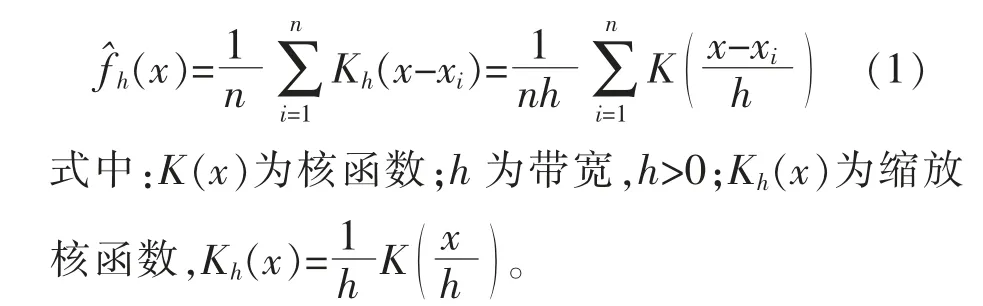
3 算例分析

以实际风电场为例， 建立风电机组的异常运行数据识别模型， 进而实现风电机组运行数据的清洗。

3.1 风电场及典型机组简况

所选风电场位于中国北方，场内共有33 台1.5 MW 的风电机组，风轮直径为82 m，风电场覆盖面积约为15 km2。风电场内地形较为平坦，机组间的最大高程差为164 m， 风电场内的机组排布如图2 所示。风电机组的切入、额定和切出风速分别为3，10.5 m/s 和25 m/s， 风电机组标准化的推力系数及功率曲线如图3 所示。

图2 风电场内机组布局Fig.2 Wind farm layout

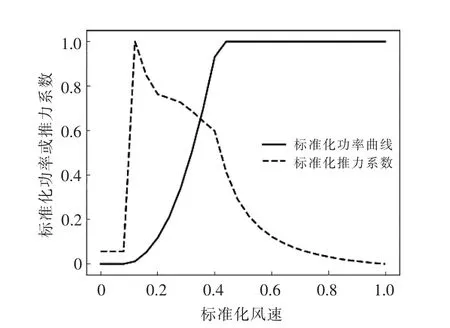
图3 风电机组推力系数及功率曲线Fig.3 Wind turbine's Ct and power curves

为完整覆盖可能的异常数据类型， 从风电场内选取4 台分别含不同异常数据种类（2～3 种）的风电机组，即1#，9#，15#和18#风电机组。4 台机组包含的异常数据类型分别为①③，①②③，①③④和①②③④，4 台机组在场内的位置由图2 中的方框标识。对2018 年5 月-12 月共计8 个月的风电机组SCADA 风速和功率数据进行归一化处理，数据的时间分辨率为10 min。

3.2 异常数据点识别

基于第2 节中方法建立异常数据识别模型，按照离群异常点、0 功率值堆积点、1 功率值低风速点和恒功率限电点的顺序， 依次识别并剔除4类异常数据，获得清洗后的风电机组运行数据。以0.05 为间隔，将（0，1]区间的标准化功率划分为20 个等间距区间。

对（0，0.95]区间的散点进行密度聚类，剔除离群点；对功率为0 的散点采用截断法处理，剔除高风速点；对（0.95，1]区间内的1 功率值堆积点采用斜率控制法处理，剔除低风速点。 针对经前3步骤（3 阶段）处理后的数据，若仍有限电堆积点，则利用KDE 模型剔除。

3.2.1 离群点识别

利用DBSCAN 模型分别对4 台机组（0，0.95]功率区间的P-V 散点进行聚类。 通过聚类合理性试验，调整最优参数，确定聚类半径Eps 为0.02，类内最小样本数MinPts 为45，聚类结果如图4 所示。 其中，黑色散点表示正常数据点，银灰色散点为DBSCAN 聚类识别出的离群噪音点。

由图4 可知，DBSCAN 方法能够较好地识别（0，0.95]功率区间内的离群异常点，以及18# 机组稀疏分布的恒功率限电点，但对于9#机组稠密分布的恒功率限电点则无法准确识别。

图4 风电机组P-V 散点图的离群点识别Fig.4 Outliers recognition for wind turbines' P-V scatters

3.2.2 0/1 功率异常点识别

图5 风电机组P-V 散点图的0/1 功率异常点识别Fig.5 0/1 power abnormal points recognition for wind turbines' P-V scatters

由图5 可知， 截断法和斜率控制法分别可以较好地识别0 功率的高风速堆积点和1 功率的低风速堆积点。 综合采用上述DBSCAN 密度聚类、截断法和斜率控制法可以有效清洗无限电状态的1# 和15# 机组以及有短时少量限电的18# 机组的运行数据， 但是无法全面清洗含有长时间限电功率堆积点的9#机组的运行数据。

3.2.3 恒功率限电点识别

针对9# 机组半清洗后的运行数据建立KDE模型开展限电数据剔除。 以功率为变量对不同区间内的P-V 散点进行密度估计，采用高斯核函数拟合散点PDF，带宽确定为0.02。 获得不同标准化功率值对应的散点分布概率密度曲线， 如图6所示。

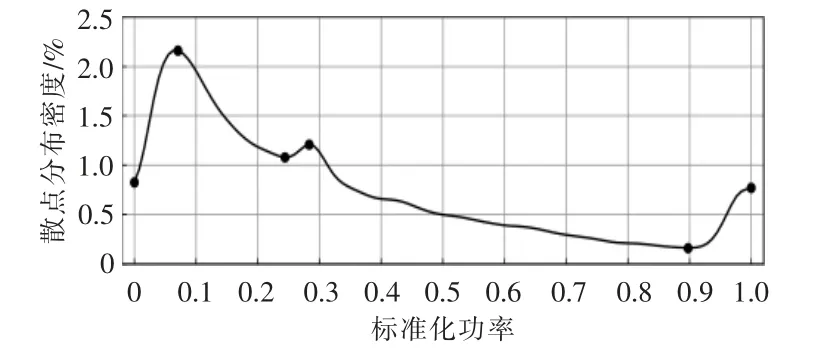
图6 不同标准化功率下的散点密度分布Fig.6 The density distributions of normalized power scatters

由图6 可知， 散点分布的密度集中区域出现在标准化功率值为0.07，0.28 和1 的位置处。结合图5（b）含限电的P-V 散点图可以看出，9# 机组的限电功率位于0.2～0.4，对应的标准化风速处于0.19～0.54。 故以0.05 为宽度，将[0.15，0.55）标准化风速区间内的散点划分为8 个等分区间。 在各个风速子区间内，沿着功率变化的方向，对区间内的散点分布进行密度估计， 获得如图7 所示的各区间散点分布的KDE 曲线。

图7 不同风速区间内沿功率增加方向的散点密度曲线Fig.7 KDE curves for normalized power under various WS intervals

由图7 可知：图7（a）～（d）中以功率为变量的KDE 曲线均呈单峰正态分布；图7（e）～（h）中以功率为变量的KDE 曲线均呈双峰分布，左侧低峰值的分布曲线则是由限电异常点引入。 根据随功率变化的密度曲线图，针对[0.35，0.40），[0.40，0.45），[0.45，0.50）和[0.50，0.55）风速区间内的散点，分别采用P=0.32，0.4，0.5 和0.7 进行截断， 也就是将区间内低于此功率值的数据点予以剔除， 强制将KDE 曲线变为单峰曲线，实现数据清洗。

经过限电散点剔除后， 获得将离群异常点、0功率堆积点、1 功率低风速点和恒功率限电点4步骤清洗后的最终数据，9# 机组清洗后的标准化P-V 散点图如图8 所示。

图8 限电的9# 机组清洗后的P-V 散点图Fig.8 Cleaned normalized P-V scatters for down-regulated 9# wind turbine

3.3 数据完整率验证

算例数据的时间覆盖范围是2018 年5 月1日-12 月31 日，时间分辨率为10 min。 各台机组的理论完整数据量、 原始数据量，1#，15#，18# 机组经3 阶段清洗后的数据量，以及含限电的9#机组经4 阶段清洗后的数据量统计如表1 所示。

表1 各台机组数据清洗前后的数据量统计Table 1 Statistics of the amounts of operation data before and after cleaning

由表1 可知： 与完整数据量相比， 各台机组SCADA 系统记录的原始数据完整率均在95%以上；4 台机组清洗后的数据量，均占原始数据量的90%以上，其中，含限电因素的9# 机组的异常数据占比最高，达8.3%。

4 结论

为充分利用有限信息提高风电机组的单机运行数据质量，本文针对风电机组实测P-V 散点图中常见的4 类异常数据点， 建立递进式异常数据识别模型。建模及分析结果表明：DBSCAN 聚类方法能够有效识别P-V 散点图中的离群异常点；截断法和斜率控制法分别可以较好地识别0 功率的高风速堆积点和1 功率的低风速异常点； 核密度估计法对限电的恒功率点识别效果显著。

经3 阶段或4 阶段的递进式数据清洗后，4台机组的P-V 散点均呈光滑的功率曲线区间带分布形式，异常数据剔除效果好，证明了本文所提方法的有效性。 各台机组清洗后的数据量均占原始数据量的90%以上，在提高数据质量的同时较好地保留了数据完整性， 进一步验证了所提方法的合理性。数据清洗是风电场控制、功率预测等研究的重要先导工作， 本文所提数据清洗方法为风电场的经济运行提供了良好的技术支持。