潮流能水平轴水轮机叶片双向流固耦合特性分析

2020-11-18徐孝辉谭俊哲张金辉于鹏鹏王树杰

可再生能源 2020年11期

袁鹏，徐孝辉，谭俊哲，张金辉，于鹏鹏，王树杰

（1.中国海洋大学工程学院，山东青岛 266100； 2.青岛市海洋可再生能源重点实验室，山东青岛 266100）

0 引言

潮流能水轮机运行于复杂的海洋环境中，在水流的影响下，水轮机的叶片结构会发生水弹性变形，而叶片结构的变化又反作用于水流的流动，对流场产生影响，干扰水轮机的正常运转，进而影响发电效率[1]。如果这种耦合作用越来越大，叶片会丧失稳定性而产生裂纹甚至断裂，这要求叶片要有较好的强度和刚度，从而对叶片结构的设计提出了较高要求[2]，[3]。因此，进行流固耦合条件下的水轮机叶片的性能分析和结构优化，对水轮机的安全稳定运行具有重要意义。

Y Bazilevs 采用风机真实工况下的风速和转速对海上风力机进行了全尺寸的双向耦合模拟，得出了风机在此工况下的动力性能以及结构性能[4]。Jong Won Lee 使用流固耦合方法对风力机叶片的气动弹性进行了研究，结果表明，随着风速和载荷的增加，叶片的弹性变形逐渐增大，气动外形也会发生明显改变，从而影响叶片的性能[5]。荆丰梅采用ANSYS 和CFX 软件进行了垂直轴潮流能水轮机的单向流固耦合瞬态计算，并完成了水轮机工作状态主轴应变计算，且计算结果与实验结果吻合较好[6]。胡丹梅采用ANSYS 软件对5 MW 离岸型风力机叶片进行了流固耦合计算，分析了额定风速下叶片的变形、推力和扭矩等参数的变化和耦合条件下叶片周围流场的变化[7]。程友良建立了海上风力机塔架叶片的耦合模型，结合Davenport 脉动风速谱，利用双向流固耦合方法，对塔架叶片的耦合结构进行了动力学参数变化分析，发现塔架叶片耦合后的叶尖位移偏移量呈脉动性变化，塔架的惯性矩较小[8]。

本文建立了20 kW 潮流能水轮机叶片的实尺度模型，采用ANSYS Fluent 模块进行了三维流场计算，使用Transient structure 模块进行了叶片结构响应计算，在每个时间步上采用System coupling 模块进行了流固耦合数据交换，得到了叶片在实际工况下的水动力学性能和结构性能，通过与不考虑流固耦合条件的计算结果进行对比分析，得到了流固耦合条件下的叶片性能的变化规律，并将仿真结果与实验结果进行对比，从而验证计算结果的准确性，为潮流能水轮机叶片的设计提供参考。

1 流固耦合的计算理论

流固耦合问题按其耦合机理可以分为两大类，一种是流固耦合作用仅发生在流体和固体交界面处，另一种是发生在流体和固体的重叠部分，并且两相域重叠在一起难以明显分开[9]。本文研究的内容属于第一类问题。

1.1 流固耦合方程

基于流体力学三大方程和理想流体及小变形假设，运用Galerkin 法对流体运动微分方程离散化，可以得到离散化后的流体运动方程式[10]：

式中：H，A，E 和B 均为系数矩阵；ρ 为流体密度；p 为压力矢量；q0为输入激励矢量；r 为位移矢量；C 为流体的压缩波速度；N 为形状函数矢量；Ω 为流体域体积；Sr 为无限远边界处的表面积；SF为自由表面处的表面积；g 为重力加速度。

与流体接触的结构运动方程式为

1.2 ANSYS workbench 耦合计算流程

ANSYS 提供的System coupling 模块可以实现Fluent 和Transient structure 的双向流固耦合计算。单向流固耦合分析在耦合交界面处的数据传递是单向的，而双向流固耦合计算既有CFD 分析计算的结果（如压力和温度）传递给固体结构分析，又有固体结构分析的结果（如位移和速度）反向传递给流体分析。由于考虑了结构变形对流场的扰动，双向流固耦合计算可以更真实地模拟水轮机叶片的运转情况。

双向流固耦合的计算采用分离解法[11]，即在每一个时间步长内，按照顺序首先在Fluent 求解器中求解流场，通过流固耦合面传递压力值给结构场，然后求解结构场，在流固耦合面处返回位移信息给流场，最后检查流场、结构场和流固耦合面处是否达到各自的收敛要求，若不收敛则返回第一步重新计算，直到达到收敛标准或最大迭代数，若收敛则进行下一时刻的计算。

2 计算模型的建立

2.1 叶片几何模型计算模型

选定斋堂岛海域作为20 kW 潮流能水平轴水轮机机组的安装区域，该岛西北部与陆地形成了一条水道，该水道深8～14 m。水轮机的额定功率为20 kW，额定流速为1.5 m/s，设计使用年限为20 a，叶片翼型为NACA63-8 系列。

水轮机的整体参数如表1 所示。

表1 水轮机整体设计参数Table 1 Overall parameters of the turbine

2.2 流场模型与结构模型的建立

图1 为叶片旋转域与流体域划分图。流体域的高度为15 m，长度为30 m，入口边界条件为速度入口，流速为1.5 m/s，水轮机叶片距离入口8 m，出口边界条件为自由出口。叶片旋转域的半径为2.8 m，长度为1 m，流体域与旋转域的交界面采用滑移网格，叶片表面设定为流固耦合交界面，采用适合水轮机的k-ω SST 模型进行计算求解[12]。

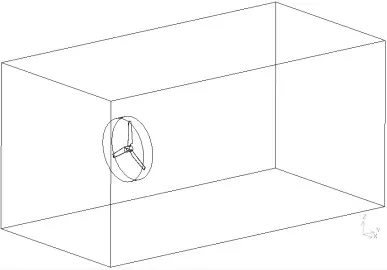
图1 叶片旋转域与流体域划分图Fig.1 Blade rotation domain and fluid domain

在叶片流固耦合问题中，由于固体结构存在变形运动，所以不仅需要耦合求解结构动力学和流体动力学方程，还要采用动网格技术不断调整计算网格来准确描述不断变化的流体和固体几何空间。在叶片旋转域采用的弹簧光顺方法是一种实现非结构网格随体变形的有效方法，计算效率较高[13]。

图2 叶片结构模型Fig.2 The model of blade structure

在Solid Works 中建立叶片结构模型（图2），叶片内部采用双腹板加横向隔板支撑。其中叶片蒙皮采用45°环氧E-玻璃纤维复合材料铺层，叶片支撑结构为结构钢。

2.3 网格无关性验证

网格划分的质量决定了计算结果的精度，也会影响计算机速度。叶片表面采用三角形网格划分，流体域和旋转域采用四面体网格划分。在稳态条件下，当网格总数为125 万～456 万时，输出功率与设计功率的相对误差如表2 所示。由表2可知，随着网格数量的增加，相对误差逐渐减小。综合考虑计算量和计算精度，选择网格总数为386 万，其中流体域网格数为313 万左右，旋转域网格数为73 万左右。

表2 网格无关性验证Table 2 Mesh independence verification

3 结果与分析

3.1 叶片水动力学性能分析

在相同的工况下，对考虑流固耦合条件以及不考虑流固耦合条件的叶片水动力学性能进行分析。

3.1.1 叶片获能效率

在尖速比不同的情况下，考虑流固耦合条件和不考虑流固耦合条件的叶片的获能效率如图3所示。从图3 可以看出，考虑流固耦合条件时，叶片的获能效率低于不考虑流固耦合条件时。这是因为在流固耦合条件下，叶片会发生水弹性变形，同时由于前后缘压差的作用，叶片形状和功角会发生改变，叶片会发生扭转变形，导致叶片获能效率降低。由此可见，在流固耦合条件下，叶片获能效率的计算值更接近于真实情况，且获能效率低于设计值。

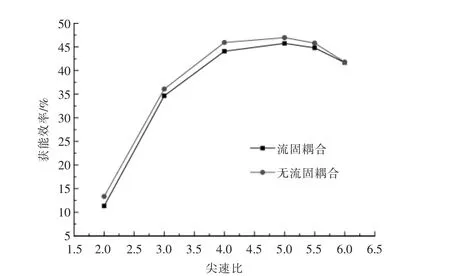
图3 不同尖速比下，流固耦合和无流固耦合叶片的获能效率对比Fig.3 Comparison of energy efficiency between coupled and uncoupled blades with different tip speed ratios

3.1.2 叶片截面表面的压力分布

当尖速比为5 时，在流固耦合与无流固耦合条件下，沿叶片展向26%，39%，53%，66%，79%和92%处的叶片截面表面的压力分布如图4 所示。

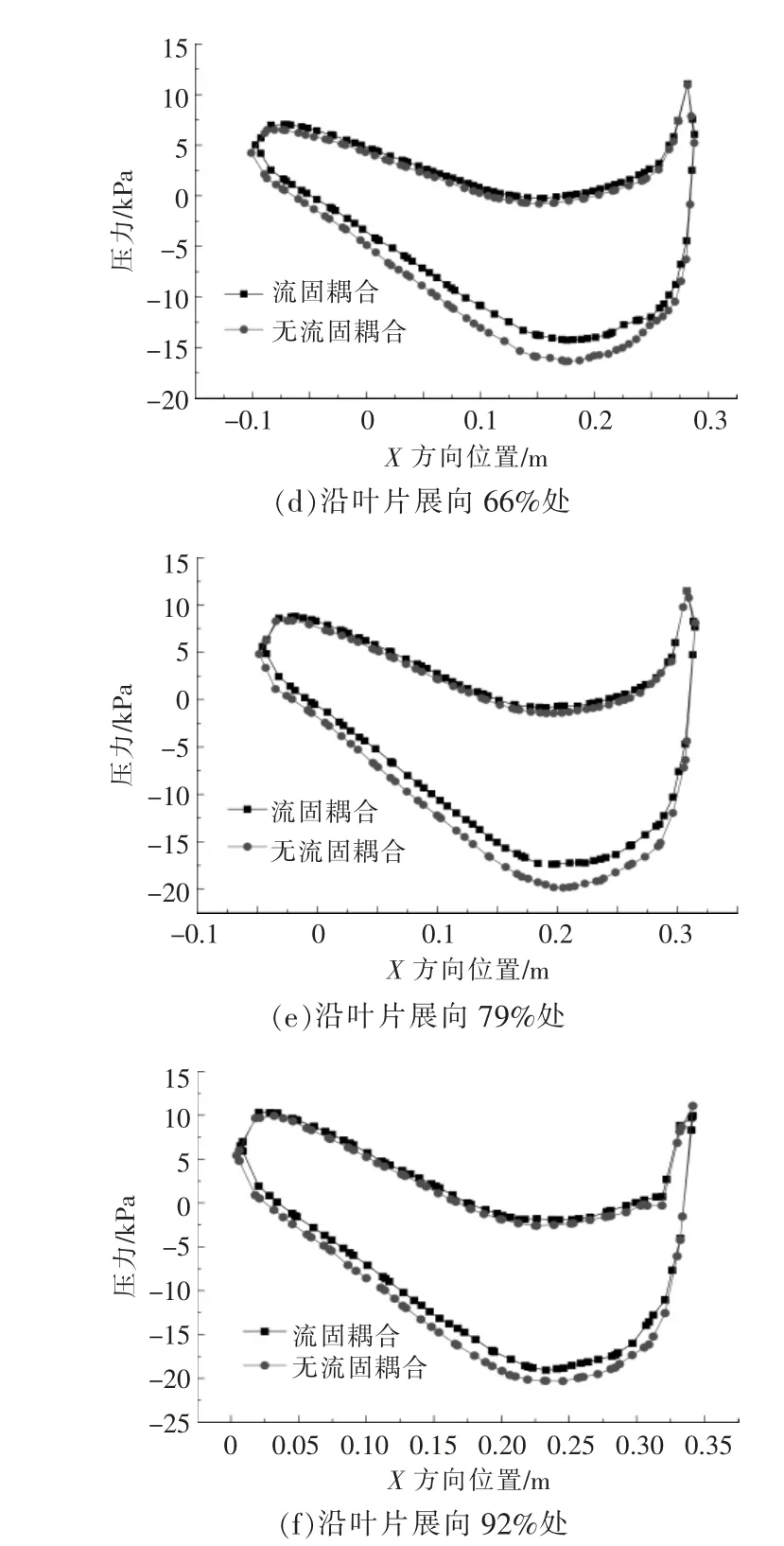
图4 叶片截面表面的压力分布Fig.4 The pressure of blade surface

从图4 可以看出，沿叶片展向，流固耦合条件下的叶片上、下表面压差与无流固耦合条件下的叶片上、下表面压差的差值呈现出先增大后减小的变化趋势。沿叶片展向39%和53%处，两种条件下的叶片上、下表面压差的差值最大，这是因为这两处的流固耦合作用最显著，在流固耦合条件下，叶片发生水弹性变形，叶片中部以及靠近叶根处应变值较大，导致叶片形状发生一定改变，影响叶片表面流场，从而导致迎流面压力降低，叶片上、下表面压差减小；而在无流固耦合条件下，叶片默认为刚体，不会产生变形，叶片表面流场不会受到结构变形的影响。在叶片展向39%以下和53%以上，两种条件下的叶片上、下表面压差逐渐减小，这说明在此长度以下叶片形状变化不大，流固耦合作用不明显，流固耦合条件下的叶片上、下表面压差与不考虑流固耦合条件时相差不大。

3.2 叶片结构力学性能分析

图5 为叶片的总体变形图。从图5 可以看出，叶片变形位移较大的区域在叶片中上部，而且越靠近叶尖，累计变形位移越大。叶片最大变形位移可达44.845 mm，因此，在设计之初就应该考虑到叶片在流固耦合条件下的变形。

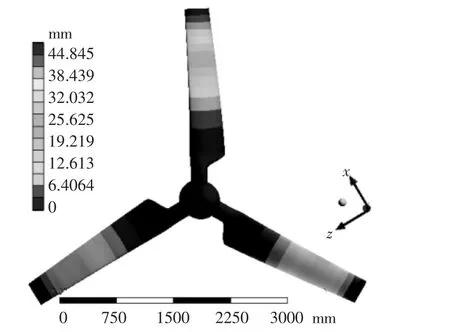
图5 叶片总体变形图Fig.5 Overall deformation of the blade

叶片在流固耦合条件下的应力及应变如图6所示。

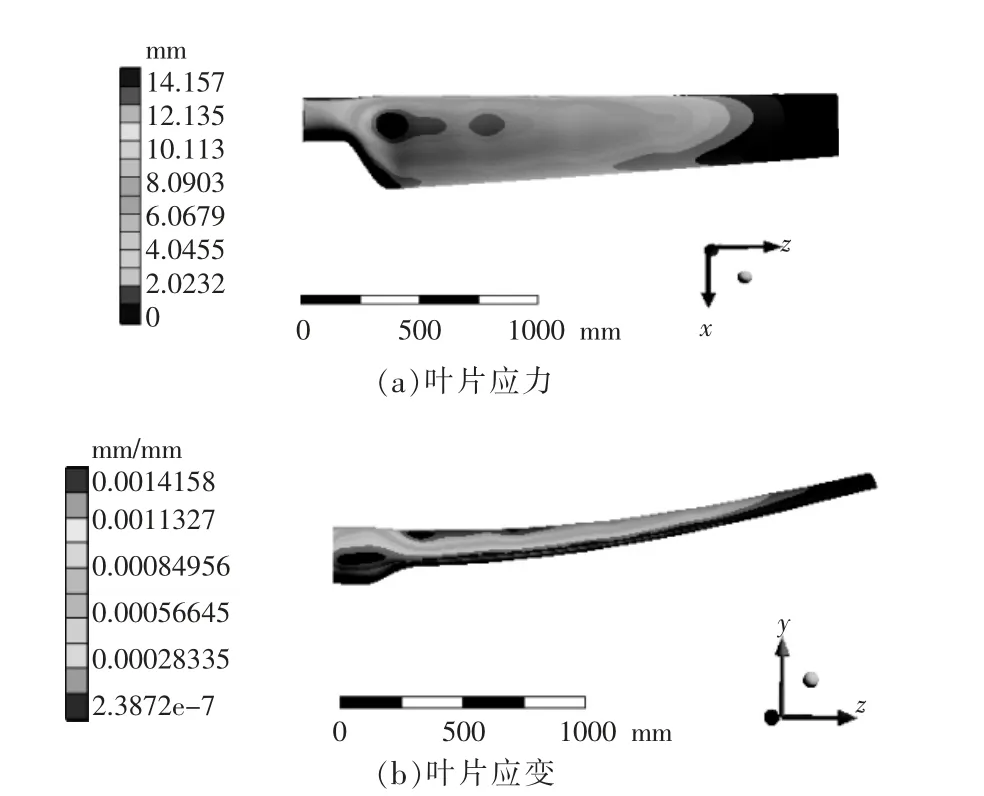
图6 叶片应力和应变云图Fig.6 Blade stress and strain diagram

从图6 可以看出，应变和应力主要集中在叶片中部和翼型叶根过渡区，即叶片中部和翼型叶根过渡区的应变较大，这会对叶片表面的流场造成影响，也进一步验证了图4 中数据的合理性。叶片内部最大应力为14.157 MPa，未超出玻璃纤维材料的弹性极限，叶片强度满足要求。

图7 叶片最大应变的变化曲线Fig.7 Maximum strain curve of the blade

耦合计算期间叶片最大应变随时间的变化曲线如图7 所示。刚开始计算时，叶片突然承受水流施加的载荷而产生了较大的应力应变，同时会出现较大位移，之后在持续水流的冲击下，初始扰动逐渐被消耗，叶片的最大应变表现出围绕平衡位置的低幅高频振动。

3.3 验证实验

为验证流固耦合计算对20 kW 潮流能水平轴水轮机水动力学性能的数值模拟结果的正确性，使用1∶5 的模型叶片进行水槽实验，根据相似原理将实验结果和数值模拟结果进行对比，以验证数值模拟结果的正确性。本次实验在中国海洋大学海洋工程实验室进行，实验水槽（图8）长30 m，宽1 m，高1.2 m。实验须要使用流速仪监测流速，使用扭矩仪测量转速和扭矩，以便计算获能效率。

图8 实验水槽Fig.8 Test sink

通过实验测得了水轮机的转速和扭矩，根据获能效率计算公式和相似原理得到了水轮机的获能效率（图9）。从图9 可以看出：考虑流固耦合条件时的计算结果更加接近于实验结果，验证了流固耦合计算方法的正确性；实验结果略低于仿真结果，这是由于数值仿真是在理想条件下进行的，而水轮机在实验过程中会受到扰动，实验结果也会受到测量装置误差的影响。