考虑广义储能的配电网双层规划研究

2020-11-18房宇娇李树静李宏仲孙伟卿

可再生能源 2020年11期

房宇娇，李树静，李宏仲，孙伟卿

（1.上海电力大学电气工程学院，上海 200082； 2.国家电网技术学院，山东济南 250002；3.上海理工大学光电信息与计算机工程学院，上海 200093）

0 前言

风、光等可再生能源发电能够有效缓解传统能源枯竭问题，但其出力往往具有随机性和间歇性，从而制约了配电网分布式电源（DG）渗透率的提高，该问题可通过调用系统灵活性资源予以改善[1]～[3]。储能（ES）、可控负荷等灵活性资源对于配电网的规划、运行以及提高可再生能源渗透率和设备利用率具有重要意义。

许多文献研究了储能及需求侧响应对配电网的影响。文献[4]利用小波变换法对ES 容量进行优化配置，从而平抑风场风机出力的短期和长期波动。文献[5]，[6]充分考虑ES 对配电网规划的影响，实现配电网扩展规划和储能选址定容的协调优化。然而，以上研究没有考虑配电网的负荷管理手段。

为综合利用多种资源，文献[7]研究了需求响应和运行控制措施对配电网规划的影响。文献[8]考虑了储能系统、电动汽车充电站与配电网的联合规划，但未考虑分布式储能成本对优化结果的影响。文献[9]，[10]将固定储能和需求侧虚拟储能视为广义储能，将其应用于分布式电源规划和广义储能规划问题中，但未对配电网网架结构进行优化。

配电网规划属于多目标优化问题。为了兼顾配电网规划经济安全和可再生能源最大消纳，充分考虑运行过程对规划结果的影响，许多学者提出了双层规划模型和求解方法。文献[11]建立了分布式光伏与储能双层协调选址定容规划模型，上层以年综合费用最小为目标，决策光伏和储能的容量和功率，下层以系统网损最小为目标，决策各节点光伏分容量和储能并网位置。文献[12]构建了主动配电网双层扩展规划模型，规划层以配电网年综合费用最低为目标，运行层以DG 消纳量最大为目标，模拟和量化了网架动态重构对规划阶段的影响。文献[13]提出的分布式电源双层优化模型，可提高计及时序运行过程的配电网规划问题的求解效率。以上研究均证明了双层模型可以将规划与运行问题有效地结合，提高求解速度与规划方案的有效性。

综上所述，基于双层规划模型，兼顾配电网经济性和DG 消纳目标，在配电网规划阶段综合考虑用户侧各类可控资源，可以提升配电网经济性，促进可再生能源消纳[14]，[15]。在此基础上，本文将储能的概念适当地外延，把蓄电池储能（BES）、可平移负荷（TL）和电动汽车集群（EVC）充电负荷等能够改变电能时空分布的设备或措施称为广义储能（GES），将其纳入配电网的规划问题中；利用含广义储能的配电网运营效率和经济性评估指标，建立了配电网规划-运行的双层优化模型。上层模型为配电网规划问题，通过优化配电网络的空间拓扑结构，便于广义储能参与优化调度。下层模型为广义储能出力优化问题，体现广义储能参与电能时空转移的能力与作用，并对上层网架规划结果进行修正。本文提出一种将传统遗传算法和风驱动优化算法嵌套的求解方法，并以某地区实际配电系统为例，验证了所提模型的可行性和有效性。

1 考虑广义储能运行的配电网评估指标

1.1 配电网运营效率评估指标

首先从配电网负载率均匀度和广义储能利用率两个方面评估配电网的运营效率，进而将其纳入到配电网的规划模型中。

（1）配电网负载率均匀度指标

配电网中大量新型负荷和DG 的接入，加大了净负荷的波动性和随机性，容易引起线路的局部阻塞。现有研究表明，电网中线路负载率越均匀，网架的承载能力越强，越能为可再生能源消纳提供可靠、便利的传输通道[4]。

式中：FN为线路负载率均匀度，FN值越小，网络运行的负载率越均匀；fi为线路i 的负载率；fave为线路平均负载率；l 为线路总数；Pi为线路i 的有功潮流；Pimax为线路i 的最大容量。

（2）广义储能利用率指标

广义储能利用率是指某一时刻广义储能充放电功率占可用总量的百分比。广义储能利用率包括充电（向上）和放电（向下）两个方面，同一时刻二者至少有一个为零。 BES 利用率如式（2）所示。

EVC 增加充电负荷等效于储能充电，减少充电负荷等效于储能放电。与TL 不同的是，EVC 负荷既具有时间分布特性，又具有空间分布特性，因此可以实现电能的时空转移。 EVC 利用率根据各时刻EV 充电数量和在站数量确定，即：

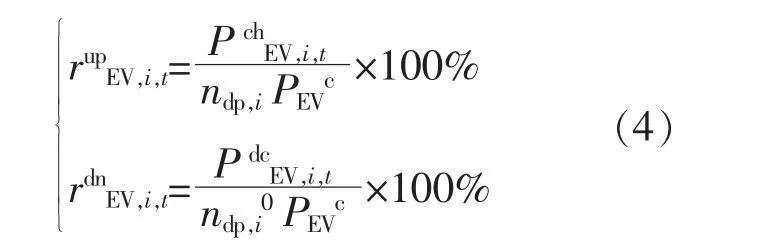
式中：PchEV，i，t，PdcEV，i，t分别为EVC 增加、减少的充电功率；PEVc为单辆EV 平均额定充电功率；ndp，i0，ndp，i分别为EV 充电数量和可参与充电的在站EV数量。

在本文优化模型中不考虑EV 对电网放电，仅对其充电负荷进行优化。

取系统广义储能平均利用率FR为优化指标，越大表示广义储能利用效率越高。

式中：T 为调度周期总时段数；Ng为广义储能节点总数。

1.2 配电网经济性评估指标

（1）成本指标

配电网总成本C 包括网架建设成本CL和广义储能成本CGES。

网架建设成本CL为

式中：ΩGES为广义储能节点集合；CaGES，i为BES 建设成本，由初始投资成本和置换投资成本组成，已有广义储能不计建设成本；SBES，i为新建BES 容量；xbes，i为节点i 处BES 决策变量； C0GES，i，t为广义储能运维成本；cBES，Cbes，TBES分别为BES 单位容量购置成本、电池本体更换成本和最大使用周期数；Pchi，t为等效充电功率；hi为广义储能补偿费用。

BES，EVC，TL 的储能补偿费用如式（9）所示。

式中：c0BES为BES 单位功率运维费用；cEV，cTL分别为EVC 和TL 参与调度的单位补贴费用。

（2）净收益指标

配电网以主动管理手段调用TL 和EVC 负荷可以就近平抑净负荷波动，实现电能时空转移，降低线路负载率不均匀程度，提高设备使用效率，从而延缓配电网设备的升级改造。可再生能源消纳水平的提高，可以减少配电网向上级电网购电成本，减少上级电网向配电网长距离输电，从而减小网络损耗。配电网净收益B 可表示为

式中：BN为每年节省的配电网升级改造费：BW为节省的向上级电网购电费；BL为节省的网损费。

式中：ΔWDG为引入广义储能后可再生能源发电消纳增量；cW为配电网向上级电网购电单价；Cinv为配电网扩建的投资成本；Ln为线路使用年限；ΔS为配电网延缓扩建年数；α 为线路负载率极差减小的比例；β 为负荷增长率；Ploss，PGES，loss分别为广义储能接入前、后的有功损耗。

2 配电网协调规划模型

由于规划与运行问题是相互响应的，因此本文采用双层规划，并在上下层之间传递相关信息。以新建线路的位置、新建BES 的配置地点、配置容量和最大输入/输出功率、广义储能等效充放电策略为优化变量；在满足电网运行约束和弃风弃光率约束的前提下，综合考虑电网规划与运行总成本、线路负载率均匀度、广义储能利用率和可再生能源消纳量，建立多目标双层规划模型。

2.1 上层规划模型

规划模型采用生成树原理生成初始网架，其结构满足辐射状与连通性约束。

2.2 下层规划模型

在上层规划确定的网架布局、BES 配置地点、容量和最大功率的基础上，下层模型以可再生能源消纳量WDG最大、违反约束惩罚量最小为优化目标；根据典型场景下的负荷数据，考虑广义储能运行约束，得到广义储能的最优运行策略。

下层目标函数如式（15）所示。式（16）～（21）分别为潮流约束、节点电压约束、线路传输容量约束、变电站容量约束、DG 出力并网量约束和弃风弃光率约束。

本文考虑的广义储能均属于能量型储能，时间间隔Δt 取1 h。下层模型中，下标s，i，t 分别表示第s 个场景、第i 个节点和第t 个时段。 pe，εe，ij分别为约束越限惩罚因子和约束越限量。 Pload，s，i，t，PDG，s，i，t，PGES，s，i，t分别为刚性负荷有功功率、DG 并网有功功率和广义储能有功出力；Gt，ij，Bt，ij分别为节点i，j 的支路导纳；θs，t，ij为节点i，j 之间的电压相角差； Vs，i，t，Vimin，Vimax分别为电压和电压限值；Pijmax为线路ij 最大允许传输功率；gmax为变电站最大容量；PDG，s，i，tmax为DG 理想有功出力；βcurt为弃风弃光率限值。

广义储能的运行约束条件如下。式中：PchGES，s，i，t，PdcGES，s，i，t为各广义储能等效充放电功率。

为避免广义储能在同一时刻既充电又放电，引入该约束令充电和放电功率至少有一个为零。

③始末电量一致性约束

在一个运行周期结束后，广义储能充电量应该等于放电量。TL 每个节点电能的移出量应当等于移入量。在整个系统EV 节点之间，EVC 增加的充电量等于减少的充电量。

式中：SOCs，i，t为t 时刻荷电状态；ξch，ξdc为BES充、放电效率；SOCmax，SOCmin为荷电状态上、下限。

3 模型的分析与求解

3.1 上下层信息传递

在上述模型中，上层的BES 规划结果通过

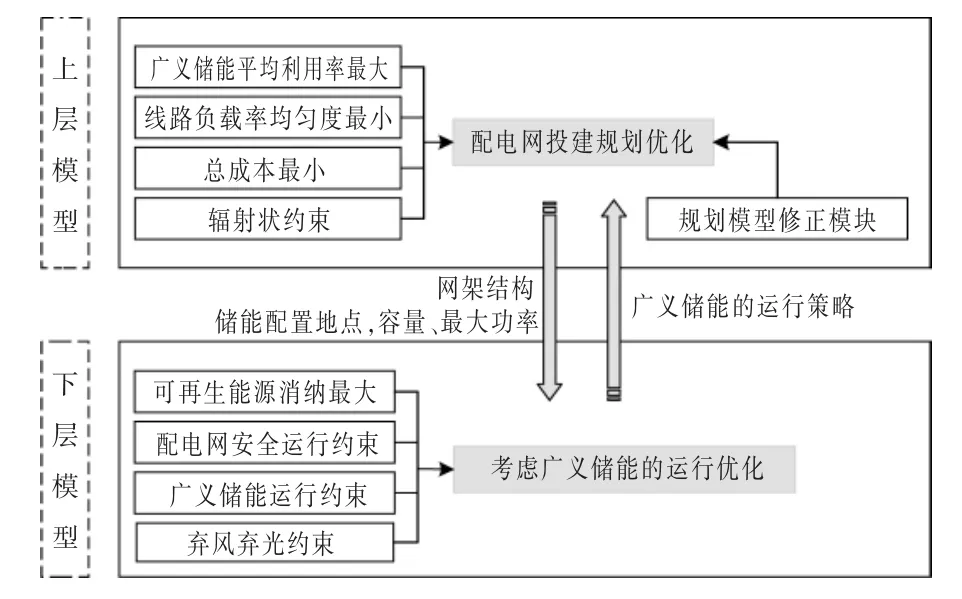
图1 双层模型关系图Fig.1 Bi-layer model diagram

为避免因线路传输容量约束越限而出现无可行解的情况，下层模型中线路传输容量约束的上、下限值引入非负的松弛变量，将近似解转变为可行解，并将越限惩罚纳入目标函数。将各时间断面下松弛变量的最大值记为εmax（lij）：

3.2 求解方法

本文采用遗传算法（Partheno-Genetic Algorithm，PGA）与风驱动优化算法（Wind Driven Optimization Algorithm，WDOA）嵌套求解双层规划模型。

上层模型采用PGA 进行求解，算法中的每条染色体由3 段基因组成，分别为配电网新建线路位置和BES 配置地点、容量、最大功率，每个染色体代表一种配电网规划方案，染色体基因组成如式（31）所示。

利用生成树方法形成初始种群中的染色体初始网络，与BES 相关的基因段采用随机法生成。

本文采用轮盘赌法选择种群中的染色体，交叉变异后得到新一代染色体，并将上层模型的目标函数转化为单目标函数作为个体的适应度函数。

式中：σ 为容许误差阀值；Fk（x），Fk-1（x）为第k 次和第k-1 次迭代后的适应度值。

由于上层模型与下层模型交替求解，因此该收敛条件既是PGA 停止的条件，也是整个双层模型停止求解的条件。

针对下层模型时间间隔小、变量维数大、约束多样性的特点，为保证快速寻优，使结果收敛，采用WDOA 求解下层模型。 WDOA 是Bayraktar Z和Werner D H 在2010 年提出的一种新的基于群体迭代的启发式全局智能搜索算法[16]。该算法的核心是模拟空气质点在大气中的受力运动，跟随空气质点的流动寻找到问题的最优解。

假设下层决策变量的维数为d，则在一个d维解的目标搜索空间中，每个可能的问题解Yi都对应一个位置，Yi称为d 维空间中的一个空气质点。由n 个代表潜在问题解的空气质点可组成一个种群：

式中：ys，tGES为第s 个典型日第t 时段广义储能充放电策略，包含BES，EV 和TL 的充放电功率大小，也表示每个空气质点在d 维空间中的位置。

对于每个可能的问题解Yi，决策变量的取值与空气质点的位置相对应，因此空气质点的位置应时刻处于优化边界内，即满足下层模型的约束条件。调用WDOA 更新其速度与位置，并计算压力函数（即适应度函数），具有最大压力值的位置将作为下层模型的最终优化解。

空气质点的速度和位置迭代方程如下：

式中：α 为固定摩擦系数；g 为重力加速度；R 为理想气体常数；T 为温度；i 为空气质点压力值排名；c 为系数；xcur，ucur分别为空气质点当前位置和速度；xopt为当前空气质点最优位置。

在该算法中，速度和位置迭代方程综合考虑了空气质点在大气中受到的摩擦力、重力、气压梯度力和自转偏向力作用[16]。算法中固定参数α，R，T，g，c 的取值参考文献[17]。

最后，将算法收敛条件设定为一个足够好的压力值。由于下层模型的目标是在保证传输容量约束不越限的基础上，尽可能使可再生能源消纳量最大，因此将下层模型的多目标函数转换为单目标函数作为该算法的压力函数（即适应度函数）。压力函数及收敛条件如式（38），（39）所示。

式中：f1*，f2*为下层模型目标函数归一化后的值；ξ1，ξ2为权重系数，且ξ1+ξ2=1；σ 为容许误差阀值；fk（y），fk-1（y）为第k 次和第k-1 次迭代后的空气质点压力值。

求解步骤如下。

①读取规划区配电系统各类数据，对上层和下层规划的决策变量进行编码，初始化算法参数。

②生成上层规划初始种群X，其中的每条染色体作为一套预选上层规划方案，开始下层优化。

③以上层某一规划方案Xi为基础，随机生成下层空气质点，并分配初始速度和位置。将式（38）作为WDOA 的压力函数，在满足下层约束条件的前提下，调用WDOA 进行优化求解得出最优下层方案yi，opt和下层压力值fi，opt，并按照式（30）修正上层参数。修改后计算上层适应度函数值Fi，opt。

④返回步骤③，直到计算出上层初始种群X中所有的规划方案。

⑤判断IPGA 是否满足收敛条件，是则转至步骤⑦，否则转至步骤⑥。

⑥选择染色体做交叉、变异，形成新一代染色体，并转回步骤③。

⑦将IPGA 最后一次迭代过程的适应度值作为最优结果，其对应的配电网规划方案和广义储能运行策略作为最优方案。

4 算例分析

4.1 算例介绍

算例为某10 kV 配电系统。该区域包括4 个变电站节点，20 个负荷节点和35 条可用廊道。区域网络结构及广义储能配置节点如图2 所示。

图2 规划区域初始图Fig.2 Planning area initial graph

设置TL 和EVC 负荷占比均为10%，DG 和BES 配置情况见表1。

表1 分布式电源和广义储能配置现状Table 1 Distributed generation and generalized energy storage configuration

结合该地区风电和光伏的四季预测出力曲线、传统负荷采用典型负荷曲线，共组成春、夏、秋、冬4 个场景用于下层优化。

4.2 规划结果及分析

采用3 种方案对模型进行求解。

方案1 仅考虑BES 与配电网的协调规划；方案2 不考虑BES，仅考虑其他广义储能资源与配电网的协调规划；方案3 综合考虑广义储能与配电网的协调规划。 3 种方案的规划结果如表2 所示。各评估指标与经济性指标如表3，4 所示。

表2 各方案规划结果Table 2 Planning results of different cases

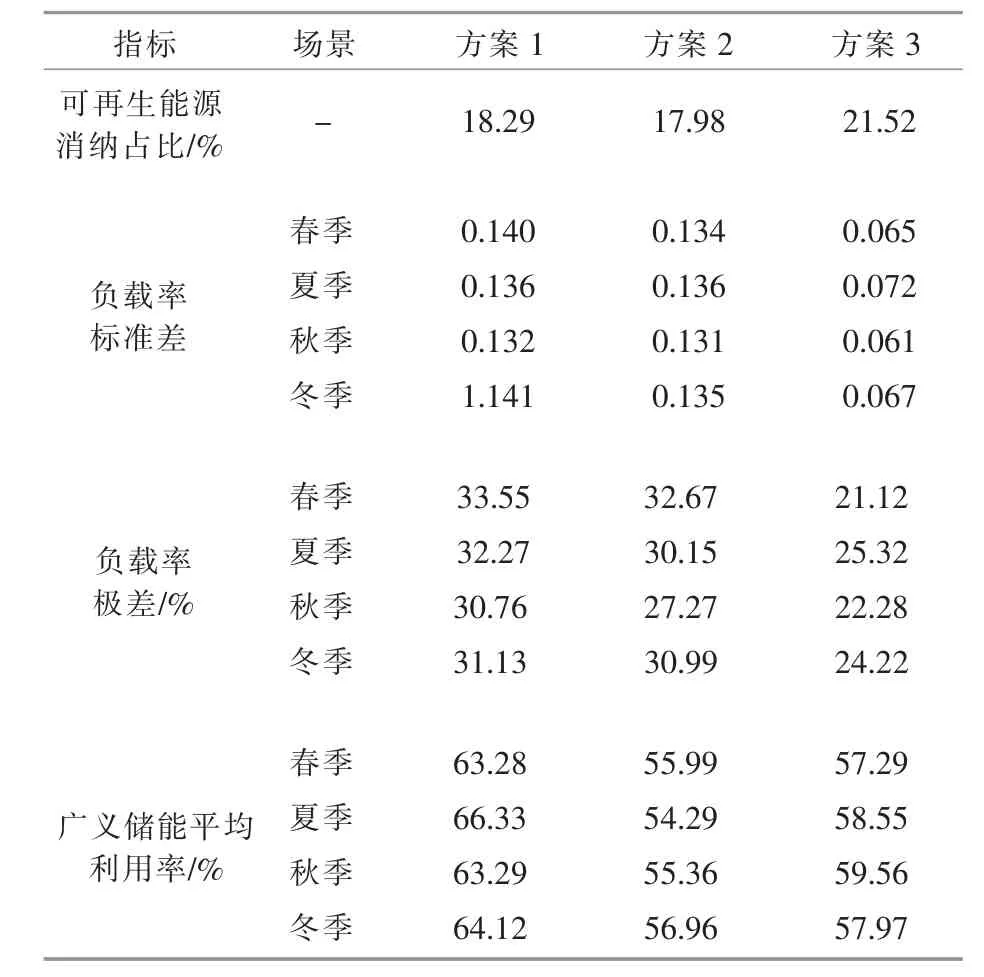
表3 不同方案评估指标对比Table 3 Comparison of optimization indicators among different cases

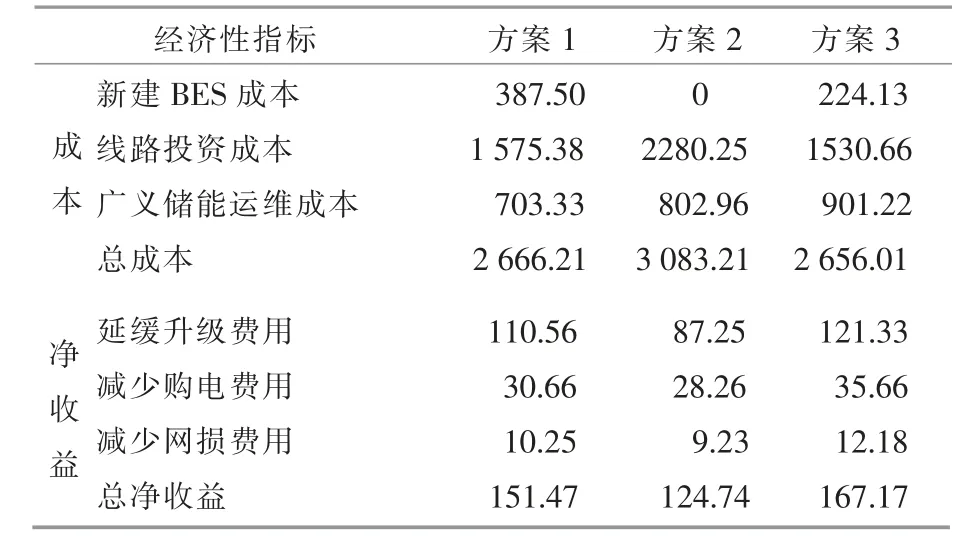
表4 不同方案经济指标对比Table 4 The cost of the planning phase of the area万元

从表3 中负载率标准差与极差指标看，方案3 最好。这是因为广义储能资源分布广泛，BES 与TL 能够就地减少负荷功率波动，EVC 负荷能够更加灵活地在EV 节点间转移负荷，同时减小了线路上传输功率的波动，改善了配电网负载率均匀度指标。

由于BES 设备调用受到的限制较少，且上层模型根据下层运行优化结果修正BES 容量，所以方案1 的BES 利用率最高；其他广义储能的调用受到原始用电规律和响应意愿等诸多因素的限制，对应方案2 的广义储能利用率相对略低。如图3 所示，方案3 的广义储能利用率为57.29%，方案2 为55.99%，方案3 中广义储能得到更加充分的利用。然而，由于该资源占总负荷的比例仅为10%，故对负荷波动的改善效果有限。

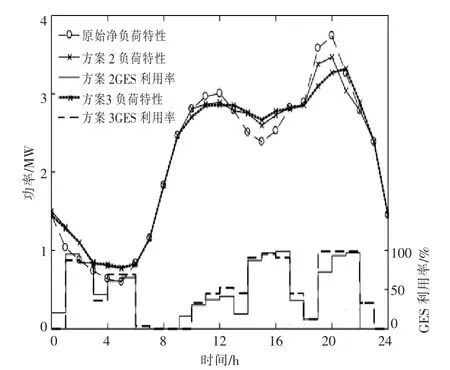
图3 节点3 广义储能利用率对比Fig.3 Comparison of GES utilization rate

方案3 中可再生能源消纳水平为21.52%，比方案1 与方案2 有所提升。通过广义储能之间的协作互补，可以吸收可再生能源富余出力，减少用户侧功率的波动，提高了DG 与负荷之间的匹配程度；同时，线路潮流的均匀分布使配电网能够进一步容纳可再生能源出力的波动，从而有效地促进可再生能源的消纳。

由表4 可以看出，方案1 不考虑其他广义储能，新建BES 的投资最大。广义储能代替一部分BES 发挥作用，减少了系统对传统储能的需求，从而降低了传统储能建设成本。方案3 新建BES 的投资比方案1 减少了42.16%。

方案2 线路投资成本最大。这是由于广义储能资源不足，当可再生能源发电无法全部就地消纳时会出现功率倒送，如果线路传输容量不足，就会导致阻塞进而影响消纳水平。为了满足弃风弃光率要求，算法寻优结果趋于投建尽可能多的线路。方案3 考虑广义储能后线路负载率极差减小，降低线路潮流越限的概率，减轻了系统阻塞，减少了配电网容量需求，从而减少了线路扩建投资。

方案3 广义储能运维成本分别比方案1、方案2 增加了28.13%和12.24%。这说明引入TL 和EVC 负荷后，运维成本有所增加。根据文献[18]，[19]可知，我国目前对TL，EVC 等可控负荷的有效调用主要采取10～100 元/kW 的补贴方式，激励用户主动转移负荷，而BES 单位运维费较少。因此，在参与调度的灵活性资源总量大致相同的情况下，仅考虑BES 的运行费用更省。

尽管方案3 运维成本较大，但是可再生能源消纳电量比方案1 增加了243.18 MW·h，比方案2 增加了302.33 MW·h。在负荷水平不变的前提下，可再生能源消纳电量增多，可以减少向上级电网购电量，节省购电费用。如果可再生能源发电量能够就近消纳，可以减少远距离输电量，从而减少网损。

综上所述，多种资源协调优化规划的效果优于单一资源优化规划。本文所提出的规划方案，通过整合和调用广义储能资源，在保证系统安全运行的前提下，提高了配电网运营效率和可再生能源消纳能力，同时也增加了电网经济效益。

为验证本文求解方法（PGA-WDOA）的有效性，选择传统遗传算法（PGA）作为对比方法，分别求解本文双层模型并对比求解效果。为兼顾算法之间可比性，两种算法都基于Matlab2017b 软件和同台计算机的环境下进行对比分析，所用算法均基于同一典型日的统计数据进行求解。对比分析结果示于表5。