基于凸集投影的视频序列单帧增强算法研究

徐梦雨

（南京理工大学紫金学院，江苏 南京 210046）

1 引言

在科学技术飞速发展的时代，通过监控系统和闭路电视系统来获取视频图像在医院、商场、银行、小区、写字楼等众多公共场所都有广泛应用。但在某些成像领域，由于受频谱混叠、光学系统相差、运动引起的模糊以及噪声等诸多因素的影响，图像往往会出现模糊和失真，难以满足某些特定领域的实际需求。改进成像设备的硬件水平是提高图像分辨率经常使用的方法，但硬件改进的成本较高，在采集视频的实际过程中难以发挥其应有的作用，就使得人们提出了利用图像增强这种软件方法来改善图像的分辨率。

在医学成像、遥感成像、人物摄影等领域，图像增强技术都有着广泛的应用[1]。传统的图像增强算法通常分为空域法和频域法两大类。例如空域法中的灰度变换、直方图均衡化和规定化等，频域法中的滤波、傅里叶变换、小波变换等[2-3]。但这些增强算法在调节图像对比度和局部增强图像细节时并没有抑制噪声的影响，获得的图像效果不能满足人们的需求。因此，研究人员提出从多个低分辨率图像序列中重建出高分辨率图像的方法，即图像超分辨率重建。1984 年，Tsai和Huang[4]首次提出了基于频率域的超分辨率重建方法。但由于模型没有考虑运动模糊、光学模糊、噪声等多种因素的影响，具有较强的局限性，这使得基于空间域的超分辨率重建算法逐渐成为研究的重点。空间域算法考虑了图像数据的空间相关性，将图像的全局或非全局运动、运动模糊、光学模糊、噪声、降采样等放入线性退化模型中考虑，因而适应性更强，适用范围更广，成为当前重建技术中的主流方法。常用的空间域图像重建方法主要有：迭代反投影法[5]、非均匀间隔样本插值法、凸集投影法(Projection Onto Convex Set,POCS)、最大后验概率估计法[6]等。

本文在对图像退化过程的建模中，针对光流场运动估计的局限性，提出采用光流场与仿射模型结合的方法进行运动的估计与配准，并采用分层高斯金字塔模型提高配准精度。针对传统凸集投影算法采用双线性插值法构建参考帧中存在的细节模糊问题，提出采用三次卷积插值和小波去噪的方法来构建参考帧，使重建后的图像具有更好的视觉效果。

2 传统的图像增强算法

2.1 分段线性灰度变换

分段线性灰度变换通过将图像的灰度区间划分为多段并分别进行线性变换，拉伸所关心部分的灰度范围，增强其对比度，压缩不关心部分的灰度范围来突出图像中用户感兴趣的灰度区间。本文采用三段线性变换，其数学表达式如公式(1)所示：

对公式(1)中灰度区间[a,b]进行拉伸，则区间[0,a]和[b,Mf]受到压缩，这两部分的图像会受到一定程度的损失。通过调节函数分段点的位置，改变直线斜率，可以对图像的灰度区间进行调节。图1给出了经过分段线性变换后的实验效果图，从图中可以看出分段线性变换在满足人们对目标区域灰度区间拉伸的同时，压缩了其他灰度区间，导致一些图像细节的损失，造成一定的图像模糊。

2.2 直方图均衡化

设r表示原图像灰度值，S表示经直方图均衡化后的图像灰度值，Pr(r)表示原图像的灰度级概率密度函数，Ps(s)表示变换后的图像灰度级概率密度函数。从S到r的反变换如公式(2)所示：

对式(2)积分并得到式(3)：

其中，Ps(s)通常为常数。图2给出了直方图均衡化的实验效果图。直方图均衡化方法通过调节图像的灰度级分布进行增强处理，增强后的图像对比度有一定的提高，但图像中存在的运动模糊和噪声问题并没有改善，在图像增强的同时降低了有用信号的对比度，从而产生了不同程度的负效应。

3 改进的光流场运动估计与配准算法

3.1 图像的退化模型

在获取数字图像的过程中，由于成像系统自身物理特性的限制或外界因素的干扰导致图像质量下降，称为图像的退化。在图像超分辨率重建中，要利用图像退化过程的先验知识来重建退化后的图像。因此，图像重建的首要任务就是正确建立图像的退化模型。本文采用图像序列的退化模型，如图3所示，这是一种比较常用的图像退化模型。在图像的退化模型中，将光学系统、传感器等多种模糊因素用扩散函数(PSF)来表示，确定PSF的类型和参数是图像超分辨率重建的基础。

3.2 基于分层迭代的光流场和仿射变换的图像配准

光流是图像灰度模式的运动表现形式，能够准确反映图像像素点的灰度变化趋势，所有的光流按空间位置排列便形成光流场。在理想的情况下，光流场可视为像素点在图像上运动而产生的瞬时速度场，因而观测者可以利用光流场来进行运动目标检测。但由于光流法是通过研究图像序列中各个像素点灰度值的时域变化来进行运动估计，因此，使用光流法应满足相邻帧亮度恒定，相邻视频帧的取帧时间连续和同一子图像的像素点具有相同运动这三个前提假设。

设I(x,y,t)表示图像像素点(x,y)在时间t处的灰度值，vx(x,y)和vy(x,y)分别表示图像在该点处的水平和垂直速度分量，在t+dt时刻该点运动到(x+dx,y+dy) ，其中dx=vxdt，dy=vydt。根据亮度恒定的假设有：

当dx、dy、dt很小时，对公式(4)进行一阶泰勒展开得公式(5)：

忽略高阶无穷小o(∙)，将公式(4)和公式(5)合并且同时除以后得到如下光流约束方程：

利用离散图像估计光流约束方程中的偏微分参数，通常采用有限差分逼近的方法。由于要保证Ix、Iy、It估计值的一致性，因此，估计时必须以同一时刻图像上的同一个像素点作为参照。Ix、Iy、It估计值如公式(7)所示：

序列图像的配准方法包括基于形状的配准和基于运动预测的配准。在基于形状的配准方法中，仿射变换法是最常用的方法，但当图像发生扭曲形变时，该方法会产生较大的配准误差。基于运动预测的配准方法主要包括光流法和块匹配法等。其中，光流法能有效克服形状匹配中物体刚性运动的局限性，但对于灰度不变的区域，无法进行光流估计。本文利用光流场和仿射变换模型相结合的方法对序列图像进行运动估计与配准，在一定程度上能有效提高运动图像的匹配精确度。

将通用的仿射六参数模型转化为易于计算的参数模型，表示如下：

其中，θ表示旋转角，(x,y)表示平动量。为了后续求解方便，令a1=cosθ,a2=sinθ,b1=x,b2=y，并分别代入公式(8)，整理后代入公式(7)得：

计算公式(9)中的参数a1、a2、b1、b2并代入公式(8)就可以估计全局运动参数x、y、θ。

当相邻帧运动位移较小时，光流估计法能较好地描述物体的实际运动情况，计算精度比较高，抗噪声能力强。在大的运动速度场中，计算量随着图像像素的增多而增大，配准的速度和稳定性随之降低。因此，本文采用4层高斯金字塔进行图像处理，实现由粗到精的参数估计。如图4所示，通过降采样分别得到原图像的1/2、1/4、1/8 倍的采样结果。然后从低分辨率层的图像开始按上述的配准算法进行参数估计，并将低分辨率图像的位移矢量估计值传递到下一级分辨率层上，作为该层配准的初始值，逐级配准，直至完成全分辨率图像的配准。由于低分辨率层的图像像素点较少，该方法能有效减少计算量，并且低分辨率图像间的位移量小于原分辨率图像间的位移量，因此，分层迭代法能用于大位移量的图像配准。

4 改进的POCS图像超分辨率重建算法

4.1 三次卷积插值法

超分辨率重建算法的实现可以分为图像序列的运动估计与配准、建立重建模型、计算高分辨率图像这三步。其中，建立重建模型就是将选取的参考帧进行初始估计。通常为了加快收敛速度，减少算法的计算量，降低对参考帧修正的次数，构造的参考帧与最终重建结果越接近越好。由于POCS算法对参考帧的初始估计依赖性较大，因此，初始估计的图像质量直接影响了POCS算法重建后的图像效果。在本文中使用三次卷积插值法来构造参考帧。

设f(x,y)表示输入图像上坐标为(x,y)的像素点的灰度值，g(x',y')表示输出图像上坐标为(x',y')像素点的灰度值。为了得到更精确的g(x',y')，三次卷积插值法使用f(x,y)周围16个邻近点进行计算。由连续信号的采样定理可知，采用插值函数s(x)=sin(πx)/(πx)对采样值进行插值，在一定程度上可以准确的恢复原函数，而三次卷积插值法采用三次多项式来近似理论上的插值函数s(x)，如公式(10)：

目标像素点的灰度值f(i+u,j+v)可由如下插值公式得到：

三次卷积插值法与最邻近域插值法和双线性插值法相比，能有效抑制插值后图像边缘的锯齿和马赛克现象。图5给出了对单帧低分辨率图像采用三次卷积插值法进行插值后的实验效果图。通过观察可以发现，利用三次卷积插值法能够较好保持图像灰度的连续性，保留高频部分的细节信息，有效抑制边缘的失真。

4.2 基于硬阈值的小波去噪法

由序列图像的退化模型可知，在图像采集和传输的过程中，受诸多因素的影响，图像中会含有不同程度的噪声，从而影响画面质量。传统的图像去噪方法通常采用滤波器来过滤噪声频率，但这种方法在低信噪比的情况下去噪效果并不理想，容易丢失图像的细节信息，从而造成图像模糊，因此，本文采用基于阈值的小波去噪方法。

小波阈值去噪方法涉及的问题主要包括三个方面：小波基的选择、阈值函数的选择、阈值的选择。通常情况下，在对图像进行小波分解时需要选取的小波具有紧支性、正交性，因此，本文选择Haar小波来对图像进行三层分解。在阈值函数的选择方面，硬阈值函数在阈值点上是不连续的，软阈值函数的原系数和分解得到的小波系数总存在常数项的偏差，在信号恢复时会损坏一些有用的高频信息，影响重构的精度。因此，本文采用基于硬阈值的小波去噪方法。在阈值选择方面，需要根据图像中具体噪声的大小合理选取阈值。在本文实验中，先对原始高分辨率图像加入模板为5×5 且方差为2的高斯低通滤波，然后加入均值为0且方差为0.002的加性高斯白噪声，从而形成降质图像。选取阈值为25.0的硬阈值函数对降质图像进行去噪处理，去噪效果如图6 所示。利用峰值信噪比(PSNR)和均方误差(MSE)来判断去噪后的图像质量，如表1所示，经过小波去噪后的图像PSNR值与降质图像的PSNR 值相比有所提高，而MSE 的值有所降低，这说明小波去噪后的图像质量与原图相比有一定提高。

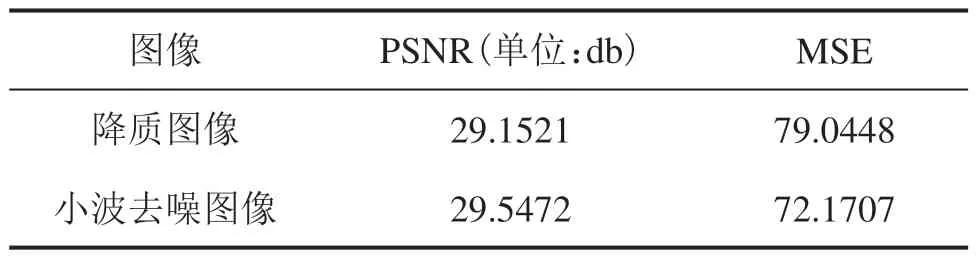
表1 图像PSNR和MSE比较

4.3 改进的POCS算法实现

利用POCS算法进行超分辨率重建的过程中需要将多帧经过运动估计和配准的低分辨率图像上的像素点投影到参考帧中正确的位置上，根据构造的参考帧在某一区域内的像素点，利用点扩散函数计算在对应的低分辨率图像中的像素估计值。若残差(估计值与实际值的误差)超过给定的阈值，就对参考帧中相应位置的像素值进行修正，经多次迭代后获得高分辨率的图像。点扩散函数PSF是凸集投影的基函数，通常假设PSF为光学成像系统中最常见的高斯函数。

设PSF 作用范围为±1 个像素点，低分辨率图像中的点(m,n)在参考帧上的对应位置为(x0,y0)，PSF进行归一化后可表示为如下形式：

设fref(x,y)表示参考帧中像素点的灰度值，y(m,n)表示低分辨率图像中像素点的灰度值，则投影像素的估计值如公式(14)所示：

投影像素点的估计值与低分辨率图像像素点的灰度值的残差r表示为：

设修正阈值为δ，fref表示如下：

将参考帧上像素点的灰度值全部修正到误差允许范围内，该过程经过N次迭代后能获得较好的高分辨率图像。图7给出了改进的POCS算法实现的基本思想。选择一帧低分辨率图像作为参考帧，通过插值和去噪对参考帧进行初始估计，根据观察图像序列对初始估计值进行循环修正，直到得到较好的重建结果。

如图8 所示，取YUV 格式视频中连续的四帧图像(352×288)进行仿真实验，第一帧图像作为参考帧，使用方差为2的5×5 高斯低通滤波核，降采样因子为2，加入均值为0，方差为0.002 的高斯白噪声，采用三次卷积插值法插值后进行基于硬阈值的小波去噪，去噪阈值设置为25.0。后三帧图像作为观察图像，使用方差为1 的5×5 高斯低通滤波核，降采样因子为2。参考帧修正阈值为1，手动设置迭代次数为6次。

图9 给出了基于改进POCS 算法的仿真实验结果，从图中可以看出经POCS 算法重建出的图像效果与降质图像相比，图像的清晰程度有明显改善，并且有效抑制了原有图像中的噪声影响。与上文中直方图均衡化算法和分段线性变换算法相比，利用POCS算法进行图像的超分辨率重建能够得到更高分辨率的图像。

5 结论

本文针对视频中的低分辨图像，提出一种改进的POCS超分辨率重建算法，系统地研究和分析了POCS算法中运动估计与配准、构造参考帧、修正参考帧这几个重要步骤。采用金字塔结构的光流场与仿射模型结合的运动估计与配准方法对大位移图像进行精确配准。在构造参考帧中采用三次卷积插值法，避免插值后图像边缘失真，并利用基于硬阈值的小波去噪方法对插值后的图像进行去噪处理。实验证明，经小波去噪后的图像与原始降质图像相比，图像质量有一定改善。将超分辨率重建后的图像与利用传统的空域图像增强算法增强后的图像进行对比，表明通过超分辨率重建技术得到的图像具有更好的视觉效果，图像质量有更加明显的改善。