中低应变率加载下弱胶结软岩动力学特性

苏宏明，王 磊，陈世官，秦 越

(西安科技大学建筑与土木工程学院，西安 710054)

我国西部矿区多为侏罗系煤层，上覆巨厚白垩系富水地层(主要是细砂岩、中砂岩、粗砂岩、砾岩及泥砂岩互层等)，这类岩层孔隙率大、胶结弱、强度低[1-3]。在矿井建设中，多采用爆破法进行开挖与掘进，而地层内含水层较多，爆破冲击荷载作用会对岩石造成损伤，出现透水、涌水等事故，造成严重经济损失。因此，对此类软岩在冲击荷载作用下的损伤特性展开研究是十分有必要的。

对于此类弱胶结软岩的研究，静力学方面，国内学者纪洪广等[4]、王渭明等[5-6]对常温状态下的单轴、三轴力学性能展开研究，指出弱胶结软岩的弹性模量、抗压强度、抗拉强度、黏聚力总体上随着埋深的增加呈线性增大，但遇水易崩解，其力学参数大多小于中东部同类岩石参数的下限；杨更社等[7-9]、李栋伟等[10-11]对常温和低温下的试验进行对比，发现这类软岩在常温状态下强度低、软化系数低、流变特征明显，而冻结下强度提升明显，脆性显著；汪仁和等[12]通过试验方法模拟了白垩系软岩在地下施工应力状态的变化过程，提出了黏弹塑非线性蠕变本构力学模型，并根据现场实测数据进行了参数反演；赵增辉等[13]采用三轴压缩试验和等效应变原理对此类软岩在复杂应力状态下的损伤行为进行研究，得到砂岩在三轴压缩下损伤变量的演化规律，并建立了考虑泥岩残余阶段变形的统计损伤本构模型。可以看出，有关此类软岩在静力学状态下的力学性质、损伤演化规律以及本构关系的研究已取得了丰硕的成果。动力学方面，Hopkinson压杆(SHPB)装置已广泛的应用于岩石类材料动力学性能方面的测试，其中杨仁树等[14-17]应用SHPB系统并结合SEM扫描实验，分析得到白垩系红砂岩动态强度随温度的变化趋势，并探究了饱水冻结红砂岩的微观破裂机制；单仁亮等[18-19]根据试验所得白垩系砂岩的动态力学特性，对其本构关系进行了研究并建立了时效损伤模型以及线性损伤粘弹性本构模型。

以上学者对于白垩系地层岩石动态力学性能和本构关系的研究奠定了坚实的基础，但杨仁树、单仁亮等研究的白垩系砂岩强度都较高，静态单轴抗压强度常温下可达30 MPa，而对于白垩系地层埋深较浅的泥质砂岩(单轴抗压强度小于15 MPa)的动力学特性及损伤演化规律研究还较少。

基于上述工程背景和研究现状，以SHPB试验系统为主体，对工程实际中最常见的干燥、饱和红砂软岩进行中低应变率下的单轴动态压缩试验，探究其力学特性和损伤演化规律，并对其本构关系进行表达，为西部矿区基础设施在冲击荷载作用下的动力响应、安全预测以及支护优化提供参考和依据。

1 单轴压缩冲击试验

1.1 试样制备

岩石取自甘肃五举煤矿白垩系地层的细粒砂岩，根据国际岩石力学学会标准，加工为φ50 mm×25 mm的标准试样(见图1)。根据试样的均匀性、完整度和光洁度进行初步筛选，分为A、B两组，A组放入烘箱中干燥24 h，B组在真空抽气机抽气12 h后放入蒸馏水中饱和48 h。再根据纵波测速仪进行二次筛选，选取纵波速度在平均值附近的试样作为试验所用，并对干燥、饱和红砂软岩试件的基本物理参数进行测量(见表1)。

图1 红砂软岩标准试件Fig.1 Red sand soft rock standard specimen

表1 红砂软岩基本物理参数

1.2 SHPB试验系统

SHPB试验系统的主体部分为φ50 mm分离式Hopkinson压杆，其组成如图2所示。试验时在入射杆与子弹的接触面张贴紫铜片，以及在试件表面涂抹凡士林，以减小试验波的弥散效应和端部效应。试验系统采集到的应变信号如图3所示，可以看出整形后的波形为半正弦式，上升沿时间较长，从而达到了恒应变率加载的试验要求，所得数据准确性和可信度高。

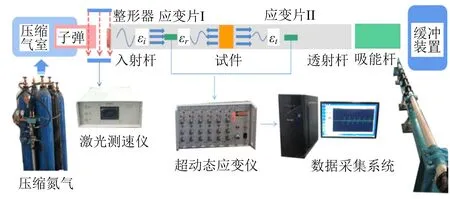
图2 SHPB试验系统Fig.2 SHPB test system

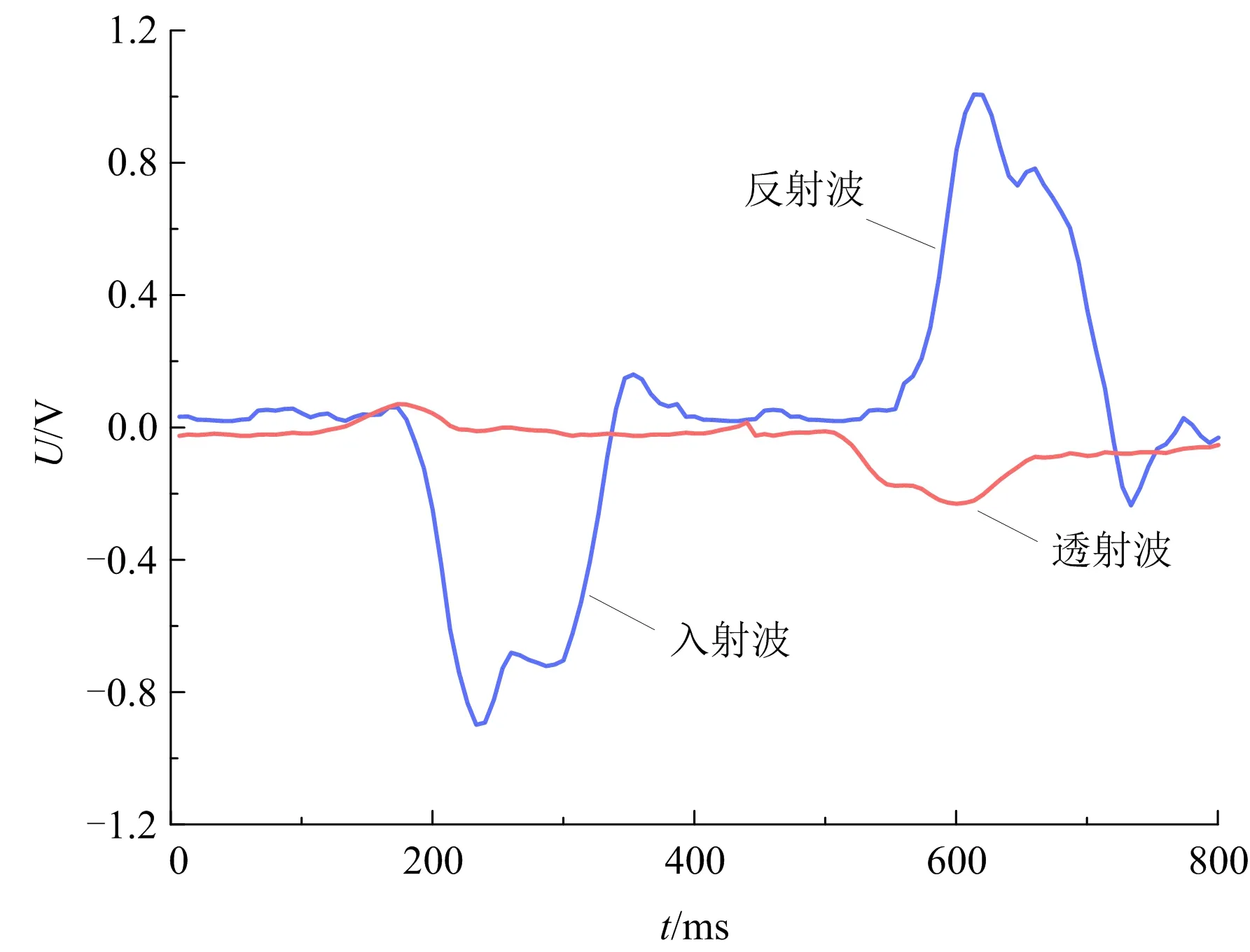
图3 电压时程Fig.3 Voltage time-history

1.3 试验方案

试验时，以0.03 MPa为起始冲击气压是因为此时的子弹速度小，对试样的扰动作用弱，而后每次增加一定大小的气压进行冲击，直至试样发生宏观破坏；为减小试验数据的离散性，每组试样个数为3，试验方案如图4所示。

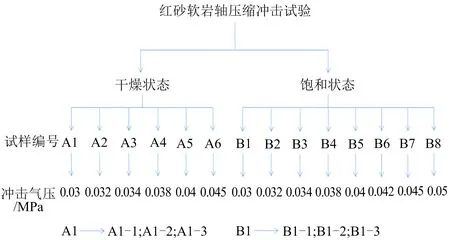
图4 冲击试验方案Fig.4 Impact test scheme

2 力学特性分析

干燥、饱和红砂软岩在中低应变率冲击下的应力应变曲线如图5所示。可以看出，干燥、饱和状态下红砂软岩的冲击曲线走势基本相同，分为典型的三阶段：线弹性阶段、应变硬化阶段和应变软化阶段；此类软岩虽然孔隙度大，但是在冲击荷载作用下应力曲线并没有表现出类似静态压缩曲线的明显压密阶段，这是因为高速冲击下，岩石内部微裂缝、微孔洞等未完全闭合，而动态应变比静态应变更快的随应力在增长，因而表现形式不同。干燥、饱和红砂软岩弹性阶段的斜率随着应变率的增加都表现出增大的趋势，即应变率效应显著(见图5)；从应变硬化阶段所占应力曲线比例来看，二者的塑性特征明显，但饱和红砂软岩表现出更强的塑性流动特性，这是应变率硬化效应、应变率强化效应和绝热升温引起的热软化效应的综合反映。

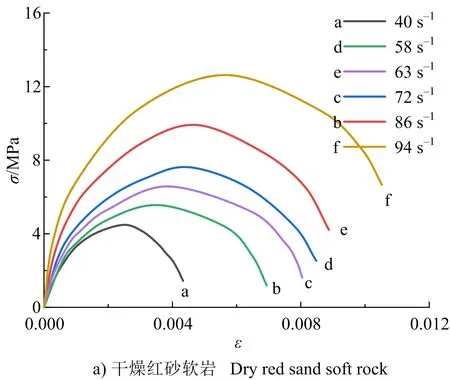
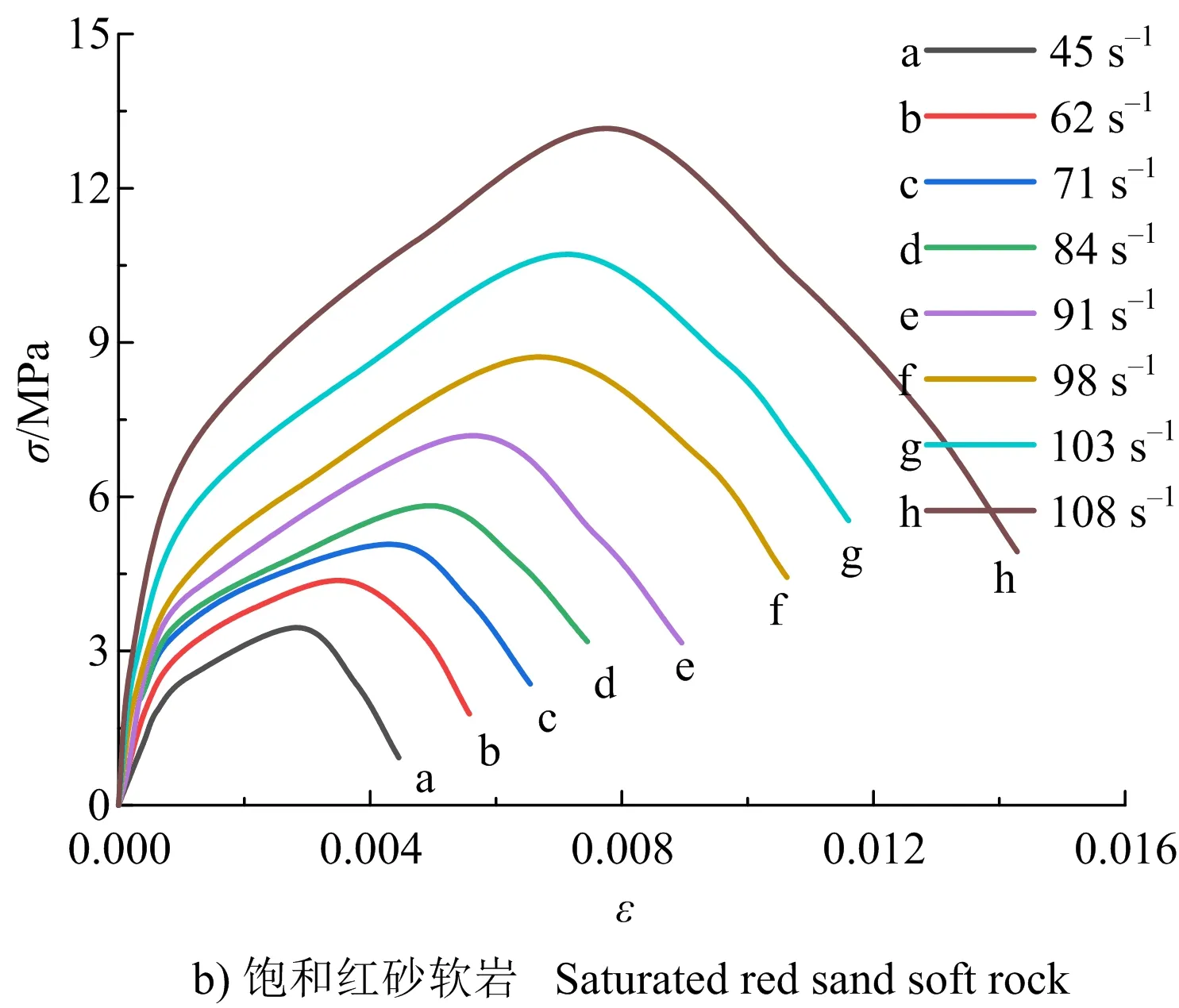
图5 红砂软岩冲击应力应变Fig.5 Shock stress-strain of red sand soft rock

干燥、饱和红砂软岩峰值应力随应变率的变化曲线如图6所示，可以看出随着应变率的增大，红砂软岩的峰值应力快速增大，两种状态下均呈指数关系，表现出明显的应变率效应，其拟合关系为

σf=0.36exp(x/28.82)+3.07，R2=0.991

干燥

(1)

σf=0.02exp(x/17.54)+3.54，R2=0.993

饱和

(2)

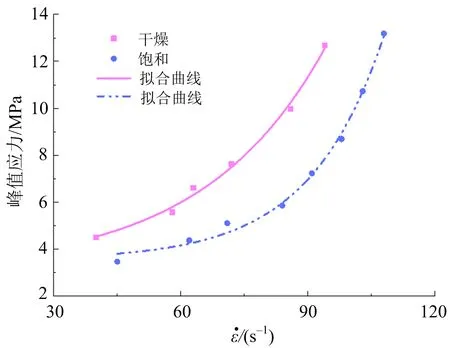
图6 峰值应力与应变率的关系Fig.6 Relationship between peak stress and strain rate

从图6可知，相同应变率下，干燥红砂软岩的强度大于饱和状态，约为1.3～1.6倍，对冲击荷载表现出更强的抵抗能力，说明水对红砂软岩主要起弱化作用，加剧了岩石内部损伤，从而使岩石力学性能下降；干燥、饱和红砂软岩产生宏观破坏的冲击气压分别为0.045 MPa和0.05 MPa，破坏强度分别为12.7 MPa和13.2 MPa，可以看出，饱和红砂软岩临界破坏强度略大于干燥试样，破坏所需要的冲击荷载也更大，这是因为饱和红砂软岩内部开口孔隙、裂纹充满了水，冲击荷载较大时，自由水来不及扩散至新产生的裂纹而使裂纹表面产生张力作用，阻碍裂纹扩展，从而岩石动态强度得以提高，试样发生宏观破坏所需的荷载也更大。

红砂软岩峰值应变与应变率的关系如图7所示。可以看出，当应变率小于70 s-1时，相同应变率下干燥、饱和红砂软岩峰值应变基本相同，表现出相同的抵抗变形的能力；应变率大于70 s-1时，相同应变率下干燥状态峰值应变小于饱和状态，饱和红砂软岩表现出更强的增韧效果和抵抗变形的能力，这与水在冲击荷载下的Stefan效应有直接的关系；红砂软岩峰值应变随应变率基本呈线性增长，但在应变率70～85 s-1处出现了转折平台，之后随着应变率的增大峰值应变对应变率的敏感性提高，表现出更强的应变率效应，这是因为应变率越大，岩石的横向惯性效应更显著，即冲击荷载作用下，岩石在惯性力的作用下保持原有的状态而限制了试件的侧向变形，使岩石处于被动围压状态，因而表现出更强的抵抗变形的能力。

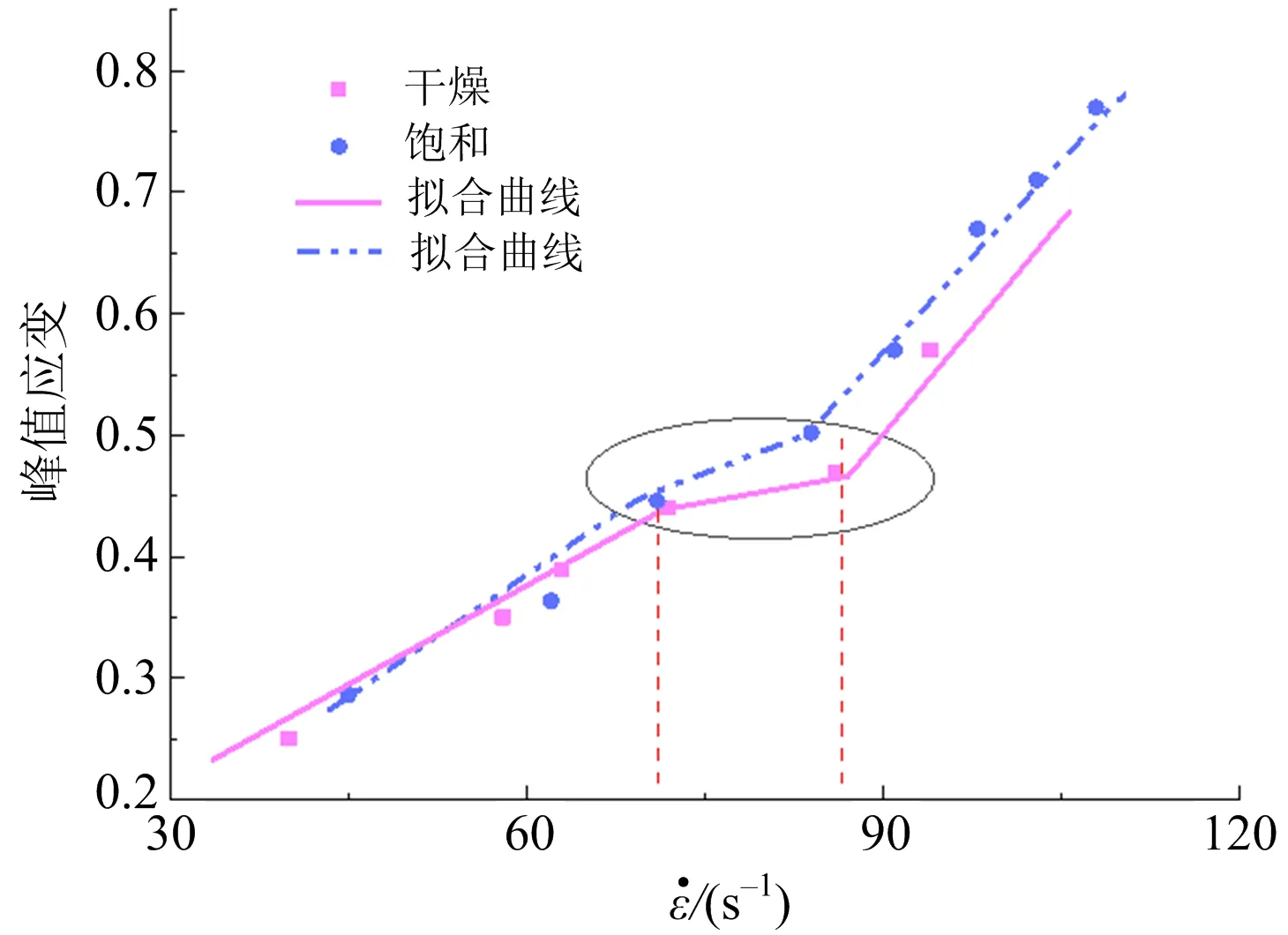
图7 峰值应变与应变率的关系Fig.7 Relationship between peak strain and strain rate

动态增长因子(DIF)作为岩石材料动力学性能分析的重要指标，计算公式如下：

(3)

(4)

式中：fd为单轴动态应力强度；fs为单轴静态应力强度；εd为单轴动态峰值应变；εs为单轴静态峰值应变。

红砂软岩动态增长因子与应变率的关系如图8所示。可以看出，干燥、饱和红砂软岩的DIF(σ)、DIF(ε)都随着应变率的增大而快速增大，表现出应变率增强效应，其中DIF(σ)与应变率基本呈指数关系，DIF(ε)与应变率呈近似线性关系；红砂软岩临界破坏时的DIF(σ)大于1，而DIF(ε)小于1，说明此类软岩在中低应变率作用下的动态强度提升不明显；低应变率下，干燥、饱和红砂软岩的DIF增长速率基本相同，这是因为此时岩石的应变与强度主要受热活化机制控制，但随着应变率的增大，饱和状态下的动态增长因子增长速率大于干燥状态，这是因为此类软岩胶结弱、强度低、孔隙率大，干燥状态下的惯性效应不明显，而饱和红砂软岩在惯性效应和Stefan效应共同作用下表现出更强的抵抗冲击的能力，因而DIF值提高的越快。

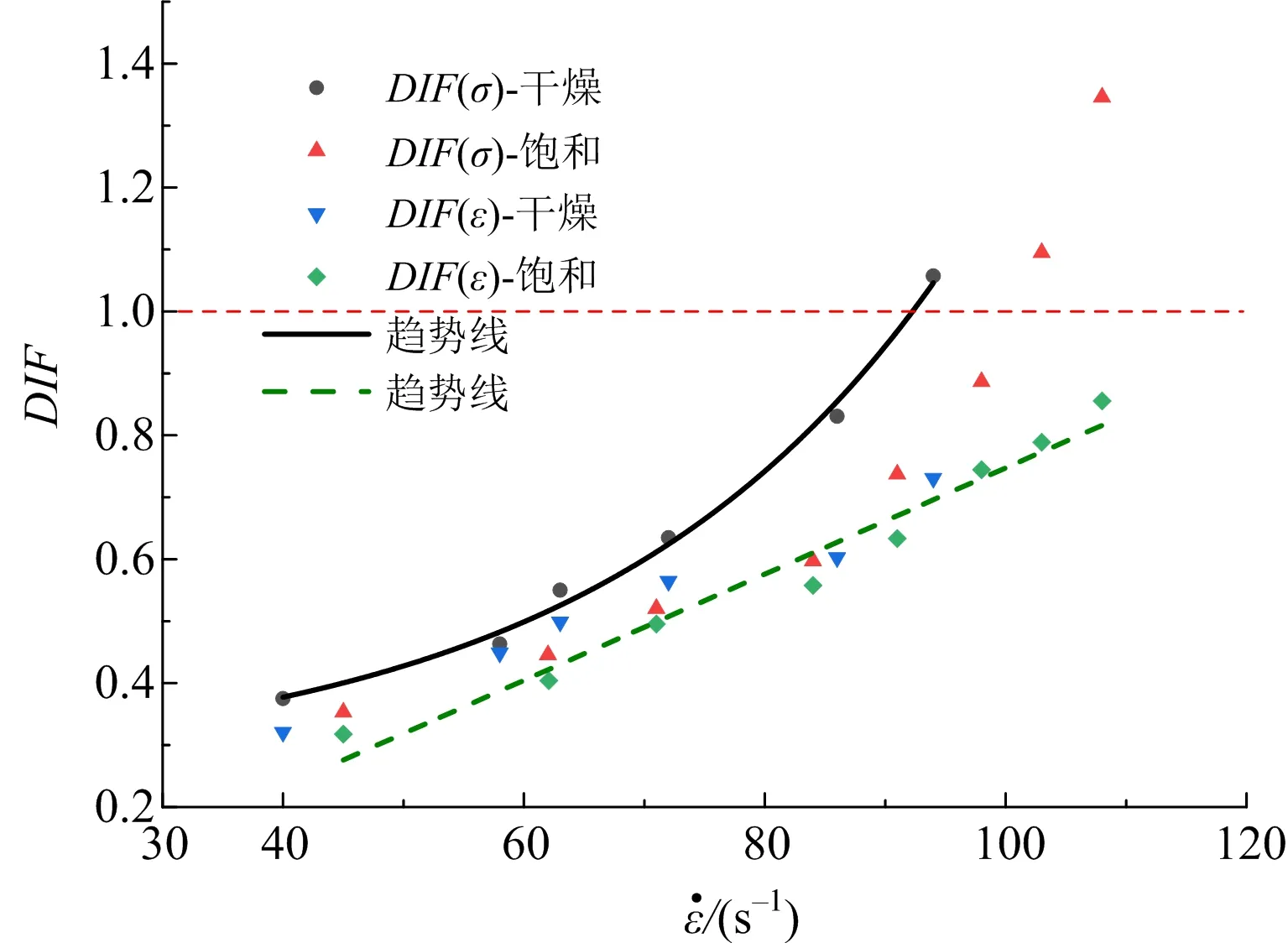
图8 动态增长因子与应变率的关系Fig.8 Relationship between DIF and strain rate

3 损伤特性及微观机理分析

3.1 损伤特性

中低应变率加载下，随着冲击荷载的增大，红砂软岩试件由完整到破碎，冲击荷载对岩石内部造成损伤，并假定试件发生宏观破坏时的损伤达到1。这里根据红砂软岩试样在冲击前后的静态单轴压缩弹性模量的变化关系来定义损伤变量，以此来衡量红砂软岩的损伤程度，即：

(5)

式中：ΔE为冲击前后模量的差值；E为未冲击时的弹性模量。

损伤变量D随峰值应力的变化趋势如图9所示。可以看出，冲击荷载作用下，干燥红砂软岩存在负损伤，以岩石初始状态定义为损伤零点，那么负损伤的出现说明低应变率作用下，内部微裂纹、微孔洞经挤压后闭合，岩石得到压缩和挤密而弹性增强，力学性能得到提高；饱和红砂软岩无负损伤出现，冲击荷载对岩石造成正损伤，说明水的存在使岩石内部微裂纹得不到闭合，反而更容易造成损伤，使其力学性能劣化；红砂软岩的损伤发展呈折线式发展，其中干燥状态下的正损伤部分与峰值应力呈线性关系，而饱和状态下出现转折点，这是由水的Stefan效应和岩石的惯性效应共同作用导致的。

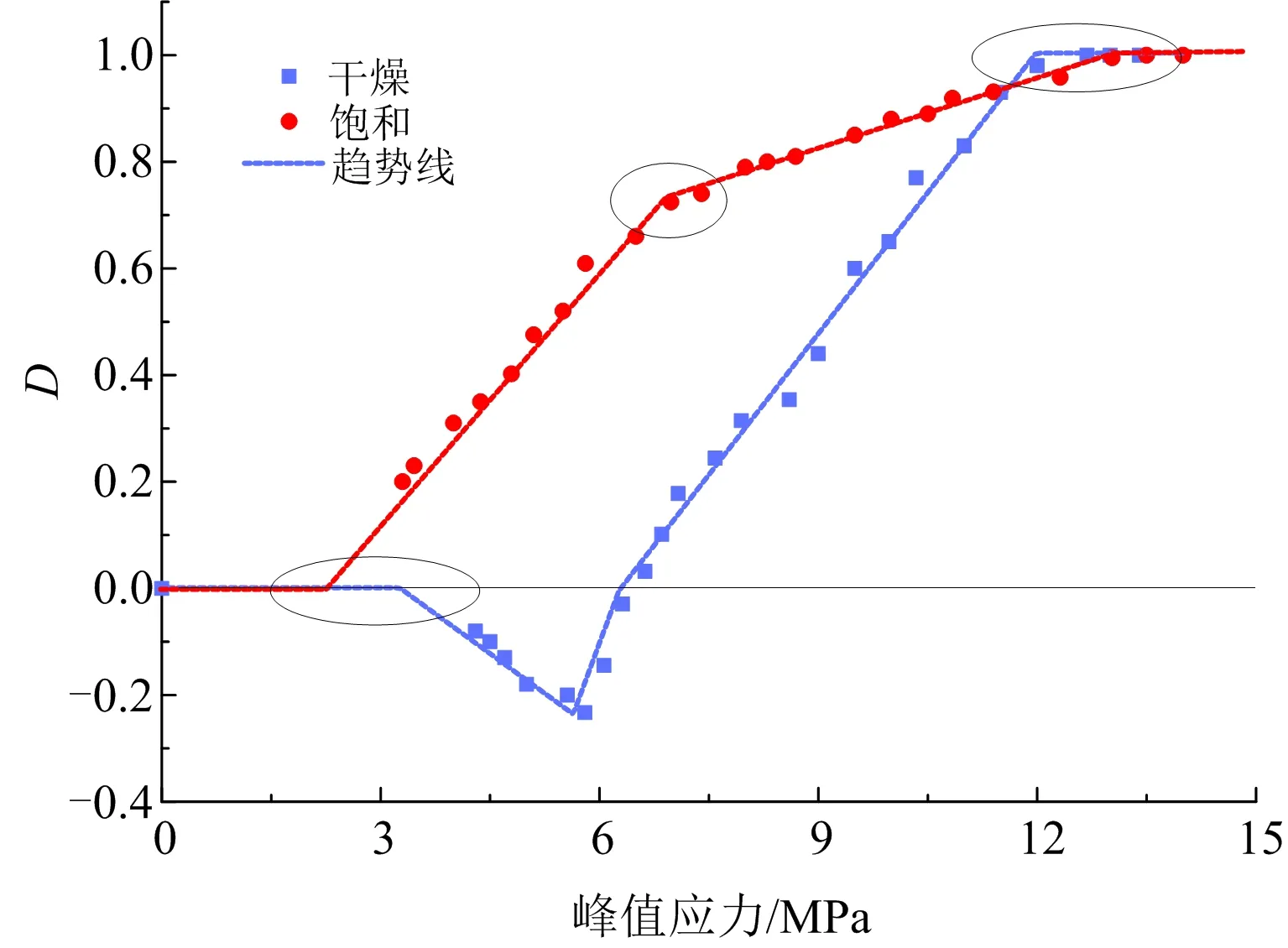
图9 损伤变量与峰值应力的关系Fig.9 Relationship between D and peak stress

根据损伤变量以及损伤阈值[20]的定义，可以看出，试验冲击荷载下未能出现损伤零点，说明此类软岩对外部作用力的敏感性高，较小的冲击荷载便会对试样造成损伤；根据损伤发展趋势线与损伤零线的交点看出，饱和红砂软岩阈值应力小于干燥状态，更说明了水在低应变率下使此类软岩力学性能劣化。

3.2 微观机理分析

红砂软岩是由岩石颗粒基质、微裂纹、微孔洞等多相介质组成的复合体，此类岩石天然状态下就存在损伤。红砂软岩在中低应变率下的宏观力学行为，可以从微观结构的损伤劣化进行分析，干燥红砂软岩微单元结构如图10所示。

注：白色部分表示微裂纹、微孔洞等损伤微元，阴影部分表示颗粒基质。图10 干燥红砂软岩微单元结构Fig.10 Micro-unit structure of dry red sand soft rock

结合红砂软岩损伤特性分析，在低应变率作用下，干燥红砂软岩内部微裂纹、微孔洞等在力的作用下闭合，岩石吸收和储存能量而得到压缩和致密，天然损伤比例减少，从而岩石强度得以提升，即出现负损伤；随着应变率的增大，由于损伤微元与周边颗粒基质的力学性质差距悬殊，外力作用下造成两者交接面处的应力集中，岩石内部损伤吸收能量后产生滑移而最先发生损伤，微裂纹、微孔洞等进一步的得到扩展，从而损伤比例增大，弱化了颗粒基质之间的胶结作用，使岩石的力学性能劣化。

水岩相互作用机理如图11所示。可以看出，在水分子进入岩石内部前，长期的地质沉积作用使岩石内部达到应力平衡状态，颗粒基质之间较为稳定且排列整齐，表现出较强的胶结作用；当水分子进入岩石内部，由于此类岩石的孔隙率很大，水分子能很快的侵入到每个基质颗粒之间， 而许多黏土矿物吸水后体积膨胀，造成颗粒基质间出现应力失衡而发生相互滑移、位错，从而导致颗粒基质间的胶结作用面积减小，只剩端部之间的一些连接，进一步的，随着时间的推移，黏土矿物的水化学反应作用使颗粒基质之间胶结力变的更弱甚至消失，产生更多的宏观损伤，颗粒基质间失去胶结作用，从而使力学性能劣化。

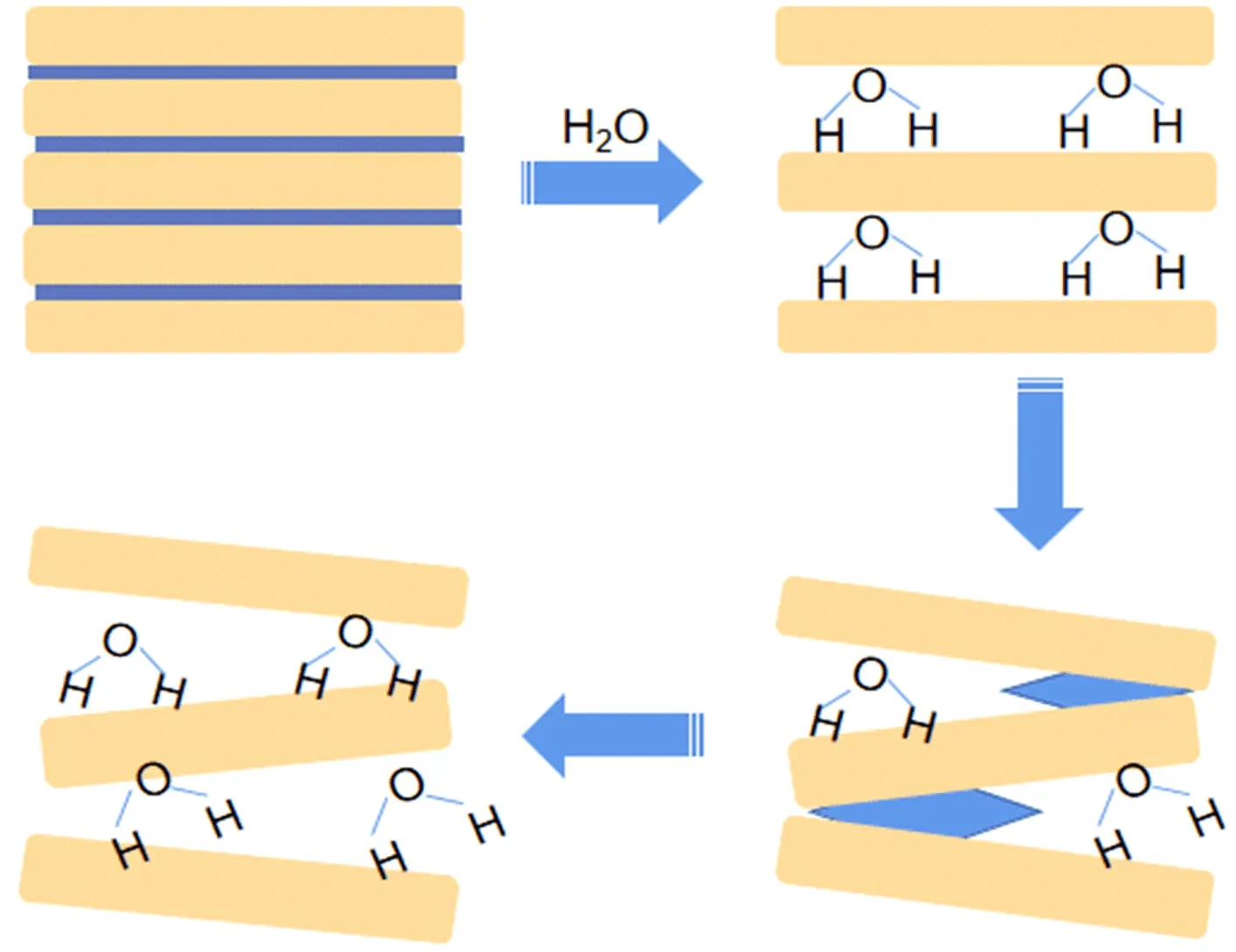
注：较浅阴影部分表示颗粒基质，较深阴影部分表示胶结作用力。图11 水岩相互作用Fig.11 Water-rock interaction

大量试验表明，岩石内部裂纹扩展是在裂纹尖端的拉应力作用下实现的。红砂软岩因其特殊的沉积过程，内部含有大量的微裂纹，较为松散的结构特征使大多数裂纹内部充满孔隙水，冲击荷载作用下，裂纹的扩展速率远大于加载速率，在裂纹尖端，自由水无法瞬间进入新产生裂纹内而使表面产生张力作用，起到了抵抗裂纹扩展的作用，因而饱和状态下红砂软岩破坏的强度高于干燥状态，且冲击荷载越大，水的Stefan效应越显著。饱和红砂软岩的微裂纹扩展如图12所示。

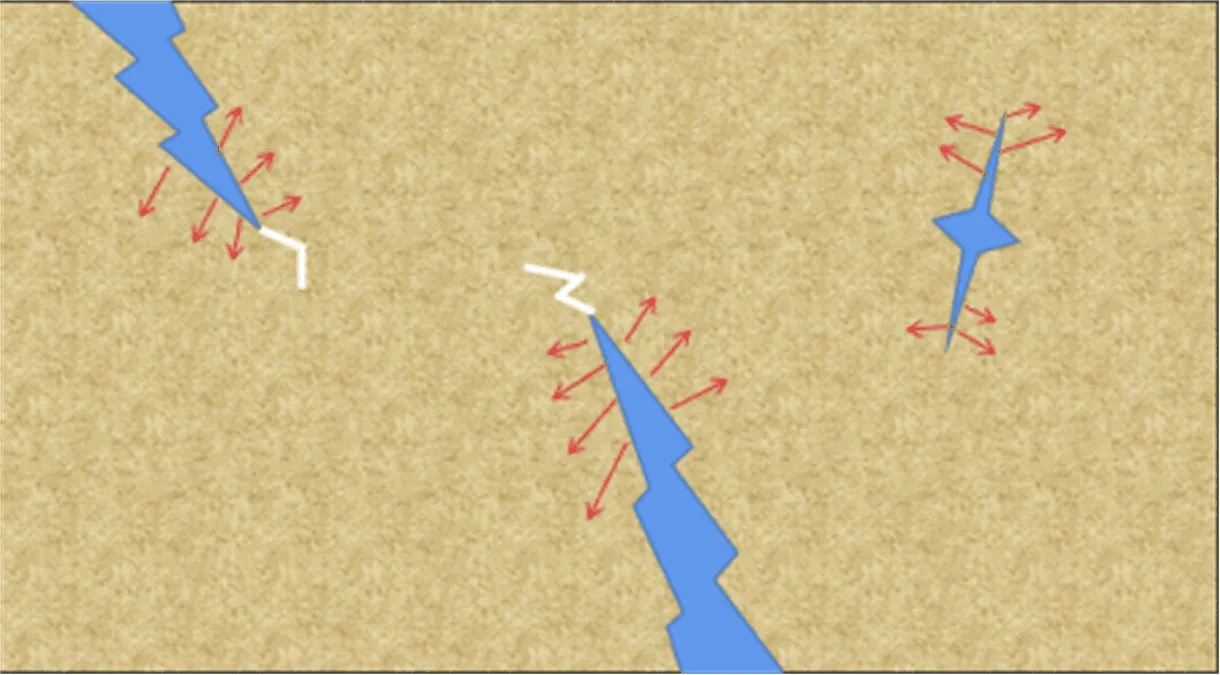
图12 饱和红砂软岩微裂纹扩展Fig.12 Micro-crack growth of saturated red sand soft rock

综合上述分析，在低应变率作用下，干燥红砂软岩的强度高于饱和状态，这是因为水对岩石的弱化作用大于Stefan效应产生的抵抗力；随着应变率的增大，水的Stefan效应和惯性效应共同作用占据了主导地位，削弱了水对岩石的弱化，从而力学性能得到提升。

4 红砂软岩损伤本构方程

朱王唐模型(Z-W-T)已广泛的应用于岩石类材料在10-4～103s-1范围内的力学性能表征，其模型由1个非线性弹簧体和2个Maxwell体组成(见图13)，其本构方程为

(6)

式中：E0，E1，E2分别为非线性体、低频Maxwell体和高频Maxwell体的弹性模量；χ，κ为非线性系数；η1，η2为粘性系数。

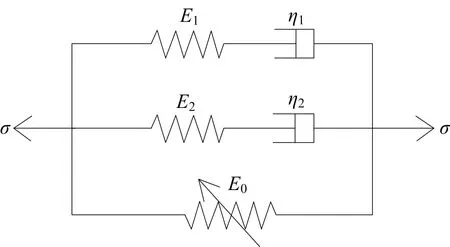
图13 Z-W-T模型Fig.13 Z-W-T model

现根据红砂软岩的力学特性对其进行改进：①根据静态单轴压缩曲线明显的非线性特征，保留其非线性体部分；②冲击荷载作用下，低频Maxwell体没有足够的时间松弛，这里看成是弹性模量为E1的简单弹簧。

改进后的Z-W-T模型本构关系表示为

σ=E0ε+χε2+κε3+E1ε+

(7)

岩石的加载过程是个不断损伤的过程，这里假设损伤微元服从Weibull分布，则损伤变量D表示为

(8)

式中：m，α为Weibull分布参数。

基于应变等效原理，可得考虑损伤的红砂软岩本构关系为

(9)

经Laplace变换后，得

(10)

现选取干燥、饱和红砂软岩各3组试验应力曲线对损伤本构方程(10)进行验证(见图14)。可以看出，改进后的损伤本构方程得到的拟合曲线与试验曲线吻合度很高，能准确的反映出此类软岩在冲击荷载下的各项力学特征。

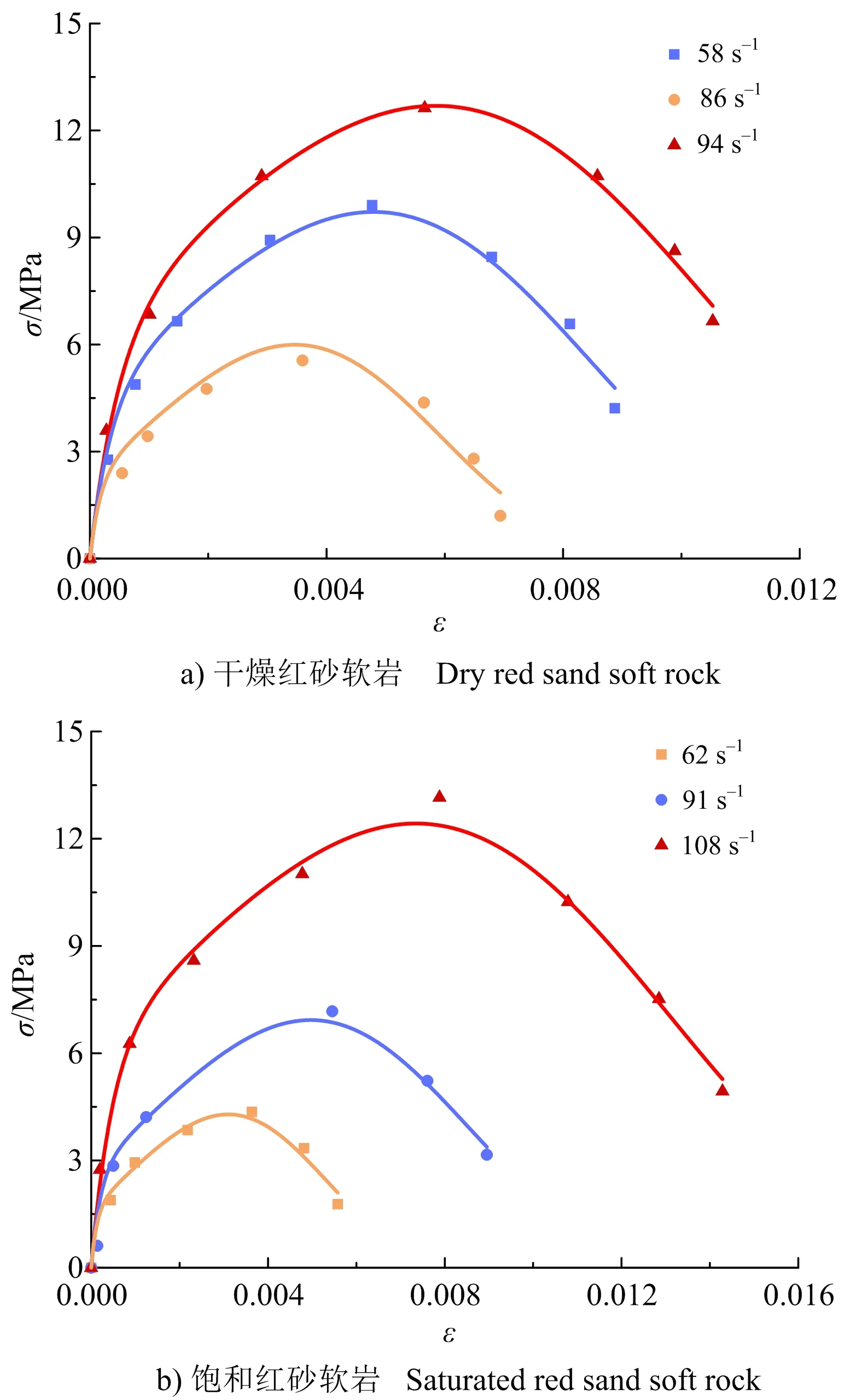
图14 损伤本构方程验证Fig.14 Verification of damage constitutive equation

本构方程(10)拟合参数如表2所示，可以看出，虽然本构方程拟合参数较多，但大部分参数为固定值，不随应变率或者红砂软岩状态的变化而变化，且E2在数值上大于E0+E1一个量级，各项拟合参数值的选取符合实际物理意义，因此所建的损伤本构关系具有一定的实际推广意义。

表2 本构方程拟合参数

5 结论

1)中低应变率加载下，红砂软岩的应力应变曲线分为线弹性阶段、应变硬化阶段和应变软化阶段；红砂软岩的峰值应力与应变率呈指数关系。

2)低应变率加载下，干燥红砂软岩出现了负损伤，饱和红砂软岩无负损伤，结合微观机理分析，低应变率下，干燥红砂软岩的强度略大于饱和状态，此时水的劣化作用占据主导地位，随着应变率的增大，在惯性效应和水的Stefan效应作用下，饱和红砂软岩的动态强度得到强化，表现出饱和红砂软岩产生宏观破坏的强度大于干燥状态。

3)基于Z-W-T模型和应变等效原理，建立了服从Weibull分布的损伤本构方程，经验证，所得拟合曲线和试验曲线吻合度良好，能很好的反映红砂软岩的动态本构关系，且各项参数符合实际物理意义，可为工程实际中相关理论计算提供一定参考。