PCA-BP算法在地面爆破振动中的应用

赵红梦，姜志侠

(长春理工大学理学院，长春130000)

随着科技的发展与进步，矿场开采等活动所引起的地面爆破振动对生产和生活环境的影响引起大众的广泛关注；目前评估地面振动以及损害最重要的两个参数为爆破质点峰值振动速度(PPV)和频率[1]。传统的地面振动研究方法是通过对爆破振动相关有效数据进行回归分析，然后通过回归分析得到的萨道夫斯基经验公式进行预测[2]，现实中质点峰值振动速度本身与很多因素有关，而常用的经验公式考虑的影响因素较少，导致其预测结果的误差较大。

基于常用公式的局限，众多学者提出应用BP神经网络算法解决预测爆破质点峰值振动速度问题[3]。其中郭连军等[4]利用优化的神经网络建立爆破的预测模型；施建俊等[5]将MATLAB与VB技术相结合，开发得到爆破质点峰值振动速度预测模型；孟陆波等[6]基于人工神经网络算法建立了爆破质点峰值振动速度预测模型；张艺峰等[7]建立了针对爆破质点峰值振动速度以及主频的预测模型。

针对目前研究现状，笔者将主成分分析(PCA)与BP神经网络算法结合在一起，提出了一种新的预测爆破质点峰值振动速度的算法,记为PCA-BP算法；其中主成分分析为一种利用降维思想提取数据中方差贡献率较大特征的方法[8]。该算法整体步骤为首先采用主成分分析方法对影响爆破质点峰值振动速度的众多因素进行分析和简化，再结合BP神经网络算法进行预测，并且将预测结果与传统经验公式预测结果进行对比分析。

1 PCA-BP算法提出

1.1 PCA算法

PCA算法最核心的思想就是降维，是通过正交变换将指标减少的多元统计分析方法[9]。

现有p个变量x1,x2,…xp，n个样品的数据阵为

(1)

(2)

将p个变量综合为p个新的综合变量，即

(3)

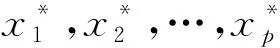
1.2 BP神经网络算法

BP算法由输入层、输出层、隐藏层3部分构成，BP算法的学习过程由正向、反向传播组成[11]。

设输入模式为x=(x1,x2,…,xn)T，算法设置隐藏层有h个单元，隐藏层的输出为y=(y1,y2,…,yh)T，输出层有m个单元，网络输出为z=(z1,z2,…,zm)T，目标输出为t=(t1,t2,…,tm)T，隐藏层到输出层的传递函数为f,输出层的传递函数为g，于是可得：

(4)

式中：yj为隐藏层第j个神经元的输出;w0j=θ,x0=-1。

(5)

式中：zk为输出层第k个神经元的输出;此时网络输出与目标输出的误差为

(6)

1.3 PCA-BP算法

首先采用PCA方法对影响爆破质点峰值振动速度的参数进行降维处理[12]，再以PCA算法计算的综合评价得分作为BP算法输入的初始数据，最后通过BP神经网络算法对爆破质点峰值振动速度进行预测。

PCA-BP算法主要步骤如下：

1)对地面爆破振动的输入数据进行标准化处理；

2)计算数据相关系数矩阵的特征向量；

3)选择p个特征向量构成主成分；

4)由主成分综合评价得分和BP参数随机选取第k个输入数据作为输入及对应期望输出；

5)利用隐藏层各神经元的输入和输出，计算误差函数ε对输出层的各神经元的偏导数和误差函数对隐含层各神经元的偏导数，分别为

6)计算从隐藏层到输出层的权值

wjk(t+1)=wjk(t)+ηδkyj，

再计算从输入层到隐藏层的权值

wij(t+1)=wij(t)+ηδjxi；

7)判断目标误差是否满足要求，当误差达到预设精度则停止计算；否则，返回到第5步，进入下一轮学习。

2 案例分析

现引用文献[5]中的20组实测地面爆破振动数据(见表1)进行研究，影响爆破振动的参数比较多，将爆心距x1、高程差x2、总药量x3、炮孔深度x4、单段最大量x5作为研究的自变量，以爆破质点峰值振动速度作为因变量，通过PCA方法提取主成分，利用BP神经网络算法进行预测。

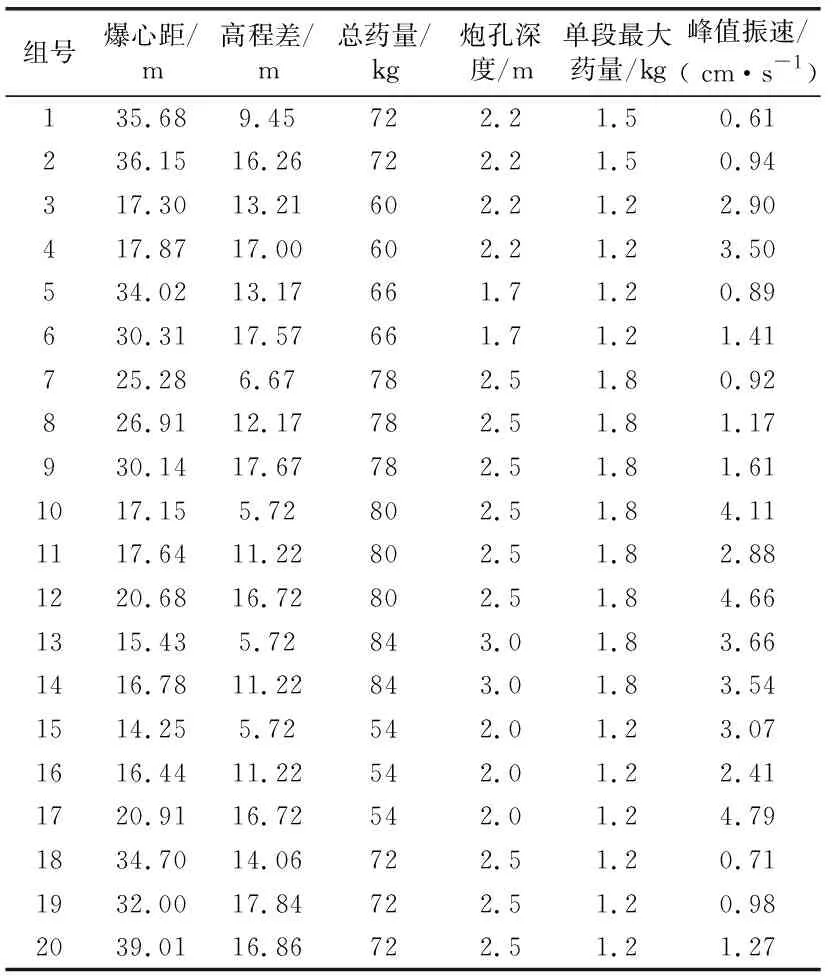
表1 爆破振动数据

表1中，选择前15组数据作为训练数据，后5组作为测试数据，通过训练数据得出的结论预测后5组数据的爆破质点峰值振动速度；并将预测结果与传统萨道夫斯基经验公式所得结果进行对比分析。

2.1 相关性分析

首先进行原始数据的标准化处理，标准化处理公式为

(7)

式中：x′为标准化后的数据;x为原始数据;u为样本均值;σ为样本标准差.

根据正态分布的基本性质，有x～N(u,σ2)，则有

(8)

原始数据集标准化为接近于正态分布(均值为0，方差为1)的数据集，然后对其数据进行相关性分析，得到相关系数如表2所示。

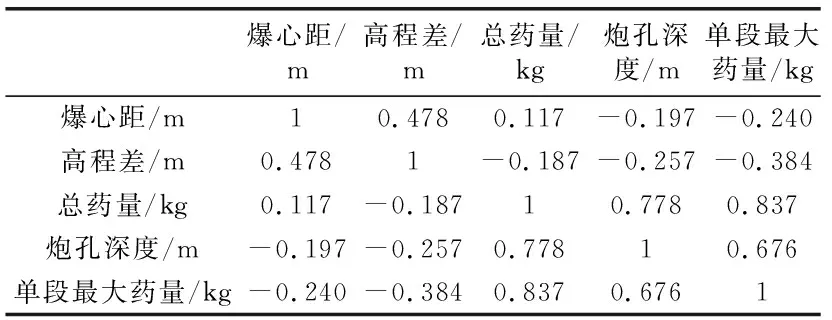
表2 相关系数

由表2知单段最大药量与总药量、炮孔深度相关系数较高，所以适合做主成分分析。

2.2 主成分分析

1)主成分选取。首先利用碎石图(见图1)选取主成分。

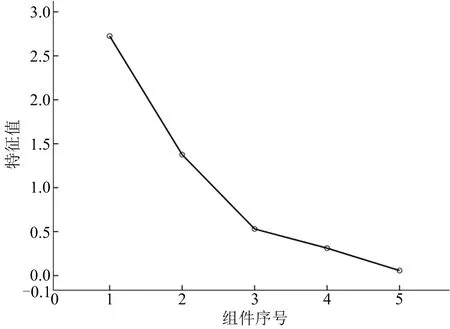
图1 碎石图Fig.1 Break store chart

由图1知，组件序号在4到5时图形区域平缓，初步判定可以选择3～4个主成分,其次进行累计方差贡献率研究(见表3)。

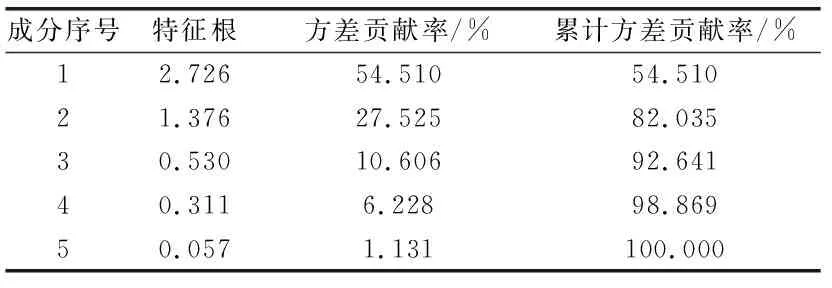
表3 累计方差贡献率

可以看出在选择3个主成分时候，保留了原始变量92.641%的信息。利用新的3个主成分代替原来的5个变量，从而起到降维的作用[13]。

2)主成分得分。第一步进行因子载荷阵的求取，利用软件得到因子载荷矩阵(见表4)。

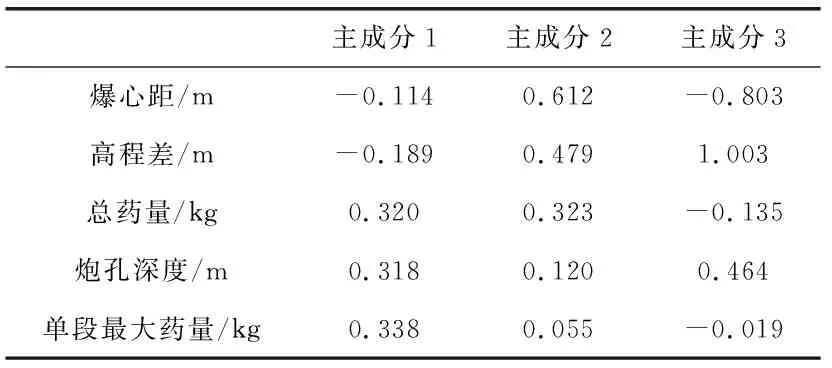
表4 因子载荷阵

根据因子载荷阵计算主成分得分公式：

(9)

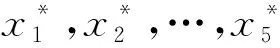
从而根据主成分得分公式以及方差贡献率分别计算20组数据的综合评价得分为：-7.04、3.21、-11.25、-5.56、-18.33、-11.53、2.38、10.6、18.76、2.38、10.66、18.82、14.15、22.38、-29.47、-21.27、-13.17、1.47、7.29、5.51。

2.3 PCA-BP算法

将主成分分析提取的3个主成分，经计算得综合评价得分作为BP算法初始数据的输入，通过训练组数据(前15组)得出的结论预测测试组(后5组)数据。构建一个3层BP神经网络对地面振动后5组数据(见表1)的爆破质点峰值振动速度进行预测，其中输入层结点数为3个，隐藏层结点数为8个，激活函数选择‘tansig’;输出层结点数为1个，激活函数选择‘logsing’。

采用梯度下降动量和自适应lr算法‘tansig’训练BP网络。学习率为0.05，目标误差为0.625×10-3，最大迭代次数为1 000，使用MATLAB软件进行计算。前15个网络输出与实际输出对比如图2所示。

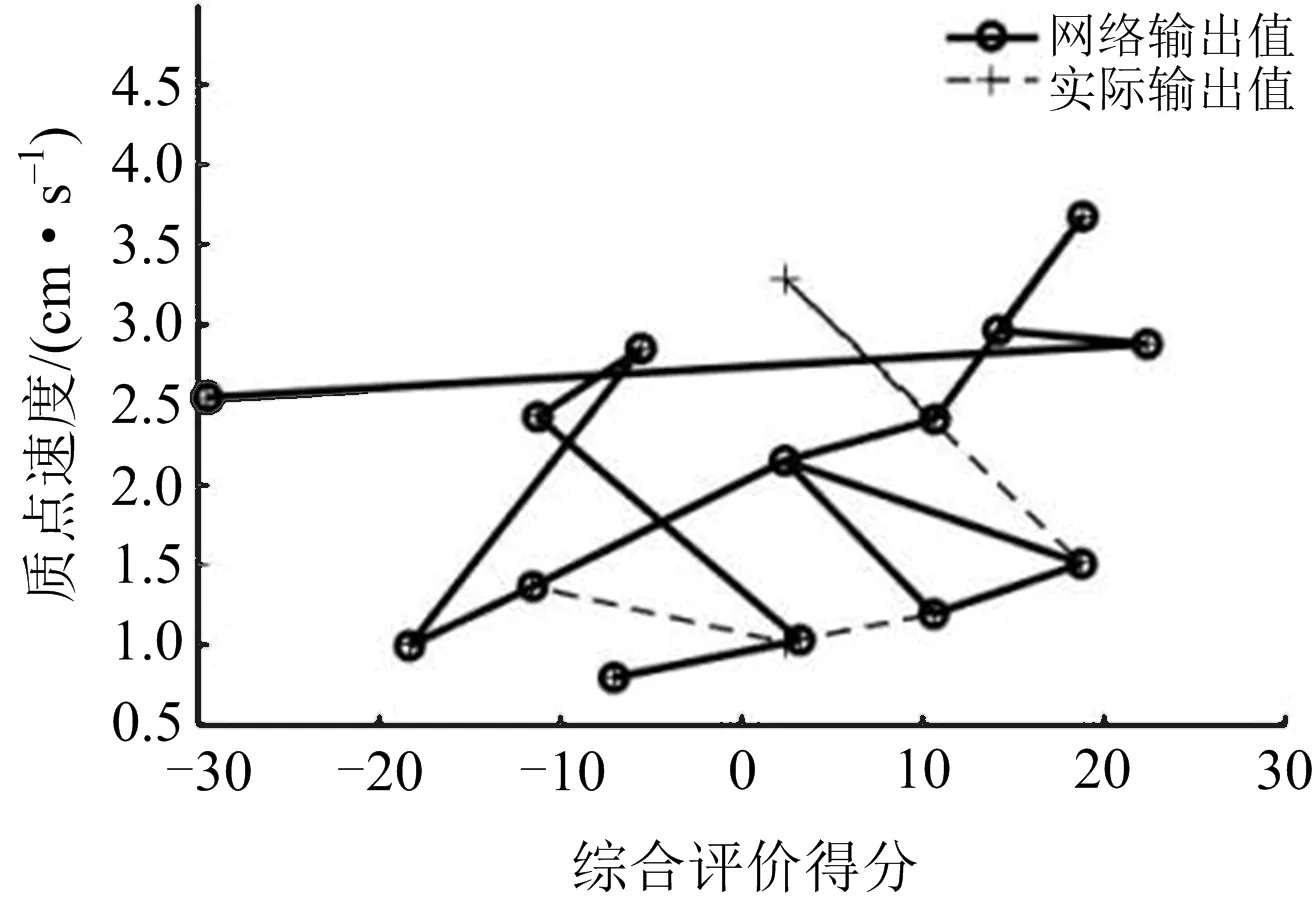
图2 前15个网络输出与实际输出对比Fig.2 Comparison of the first 15 network outputs and the actual output

地面爆破质点峰值振动速度预测结果与期望目标的关系如图3所示。

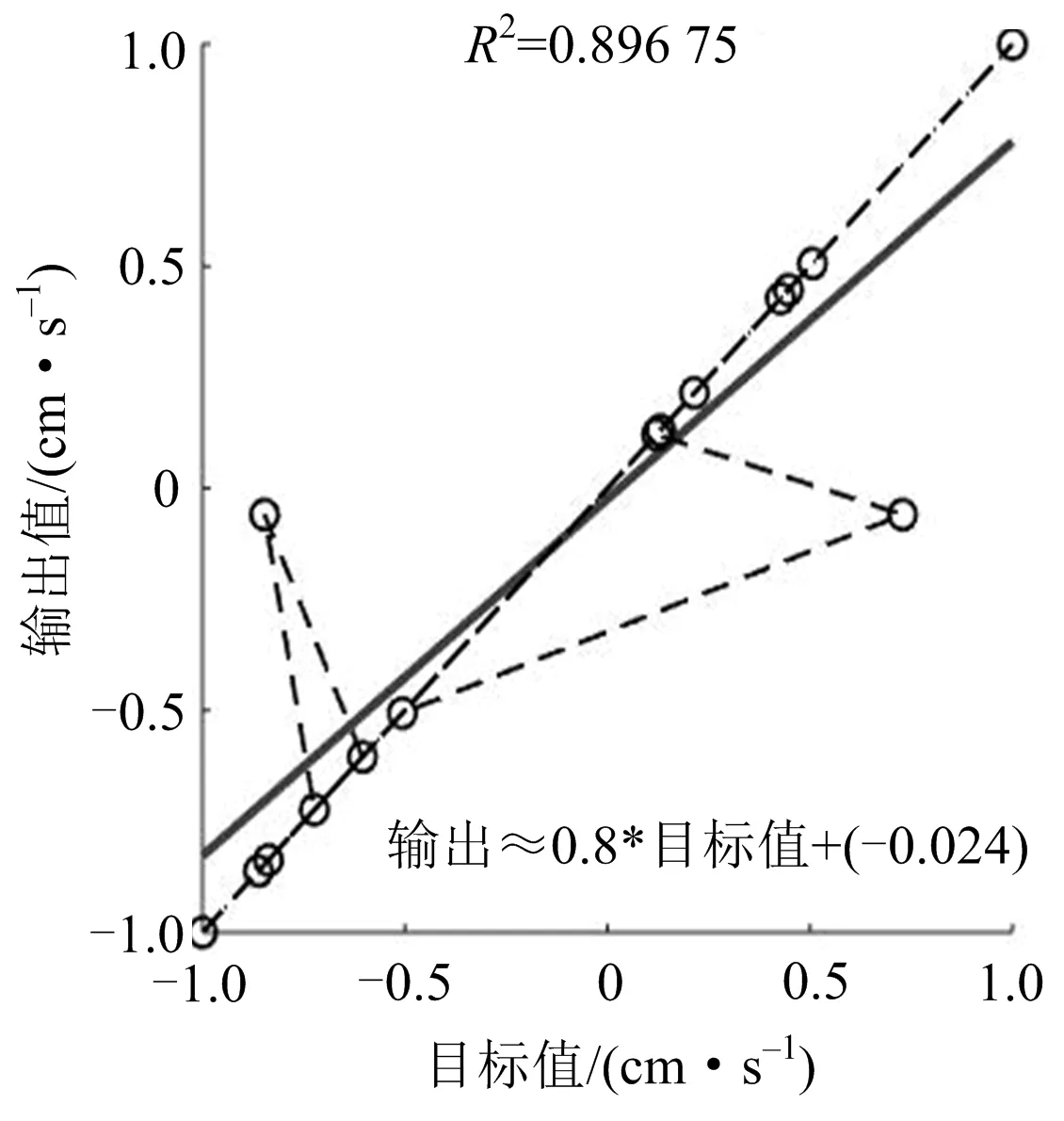
注：实直线为预测结果拟合的线性曲线，散点图构成的虚线为实际值拟合而成。图3 振速预测与期望目标关系Fig.3 Relationship between vibration speed prediction and desired target

利用PCA-BP算法经MATLAB计算可得测试数据(后5组)预测结果值分别为2.349 2、4.929 6、0.771 2、1.150 3、1.421 4。将预测结果与期望目标拟合成线性函数，计算得二者的相关系数达到 0.896 75(理想状态是相关系数等于1时)[13]，说明预测结果的可信度较高。

3 对比分析

传统萨道夫斯基经验公式[14]为

(10)

式中：k,α为经验系数；Q为单段药量；R为测点到爆心的距离。

从而利用对数变换

(11)

令

公式变为回归方程

y=b+αx

从而得到预测公式为

y=2.551+1.747x

(12)

利用传统经验公式计算后5组数据预测结果为1.60、1.34、0.91、0.97、0.83，具体回归分析结果如表5所示。

表5 回归分析结果

将传统萨道夫斯基经验公式[15]以及PCA-BP算法预测结果进行对比分析(见表6)，这里以测试数据(后5组)预测结果的相对误差、平均误差作为参照，可看出利用PCA-BP算法预测的相对误差分别为2.52%、2.83%、7.94%、14.80%、10.65%，平均相对误差为7.748%；传统经验公式的相对误差较高，分别为33.61%、72.03%、21.97%、1.02%、34.64%，平均相对误差为32.654%；除了第19组的相对误差略高于用传统经验公式预测的相对误差外，其他组利用PCA-BP算法预测的相对误差均较小；这说明PCA-BP算法预测模型有效性较高。

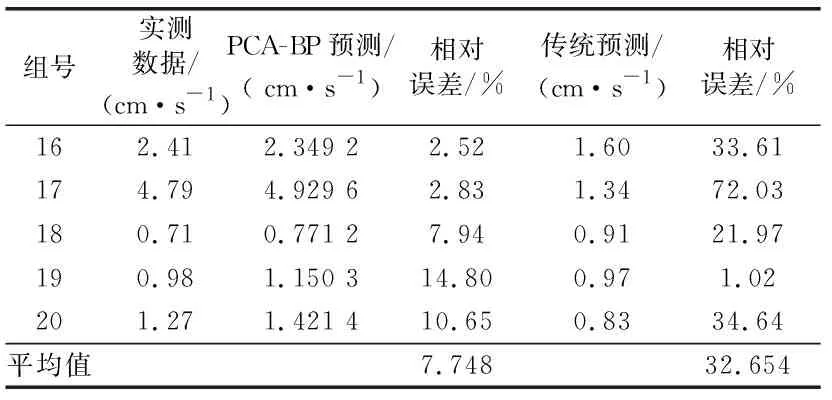
表6 预测结果对比分析

4 结语

PCA-BP算法解决了在预测爆破质点峰值振动速度中输入数据较多，各个输入变量之间存在多重共线性和相关性的问题。在案例分析中，通过对输入数据进行主成分分析提取主成分特征向量，计算综合评价得分作为BP算法的输入，并与传统萨道夫斯基经验公式预测相比，PCA-BP 算法综合考虑影响地面爆破振动的因素，使得预测结果更加合理，结合主成分分析和BP神经网络算法的预测结果平均相对误差为7.748%，小于用萨道夫斯基经验公式进行预测的平均相对误差32.654%，故说明，将PCA-BP算法应用到爆破振动工作中是比较可行的。