部分螺旋桨工作状态下的船舶性能仿真研究

郝 璇，赵玉娇，王兴龙

（招商局重工（江苏）有限公司，江苏南通 226100）

0 引言

随着航行船舶的载重吨和功率不断增加，船机桨匹配性研究尤为重要。对多机多桨船舶，运行时可能存在只有一部分螺旋桨工作的情况。非工作状态下螺旋桨包括锁轴和脱轴。锁轴意味着螺旋桨被锁住，不能转动，脱轴意味着轴系与主机脱开，螺旋桨在水流冲刷作用下自由旋转。目前船机桨模型的研究，多针对特定的母型船，通用性较差，并且主要关注对象为正常海况下正车正航时的船桨工作特性，对于非正常工况下的研究较少涉及。

在船舶设计阶段引入仿真实验，以检验船机桨匹配特性，预报各种典型工况下的航速、推力和扭矩是目前比较先进的做法。在船舶设计的初始阶段，船舶的水动力数据难以取得，一般只有船机桨的基本参数。基于这些基本参数，本文尝试建立适用于不同船型的通用船机桨模型，模拟非正常工况下的船机桨匹配特性。

1 部分螺旋桨工况下的数值计算

在对螺旋桨进行精细建模的基础上，采用CFD（Computational Fluid Dynamics，计算流体力学）方法计算螺旋桨水动力性能，通常能获得较精确的结果。而在没有螺旋桨细致的结构资料情况下，采用卡耳玛柯夫经验公式进行估算是唯一可行选择。

1.1 锁轴工况

锁轴状态，也就是当多个螺旋桨共同工作时，由于某个螺旋桨不能正常工作而被刹车装置锁死。俄国科学家卡耳玛柯夫对部分螺旋桨工作状态总结出以下公式：

式中 Rp——螺旋桨受到的阻力

A/Ad——盘面比

Vp——来流速度

D——螺旋桨直径

g——重力加速度

根据卡耳玛柯夫公式，定距螺旋桨的阻力与来流速度和螺旋桨的形状均有关系。螺旋桨受到的阻力随进速成正比关系，螺旋桨的直径与阻力亦成正比关系。

卡耳玛柯夫公式虽然在大量实验结果基础上，总结的公式得到了很好验证，但仍然存在一定误差。根据卡耳玛柯夫公式，船舶双内桨锁定和双外桨锁定的阻力值理论上是相同的。但是，如果考虑到船舶航行时在船舶周围，特别是在船舶尾部随着一股不均匀的伴流影响。由于半流在圆周上的不均匀性，使内外螺旋桨受到不同的伴流，因此内桨锁定时受到的阻力值小于外桨锁定时受到的阻力值。故在实际计算中，内桨阻力公式修正为，其中，K锁是小于1 的修正系数。

1.2 脱轴工况

脱轴状态下，螺旋桨与主机轴承脱离，不用刹车装置刹住螺旋桨，此时，螺旋桨处于自由旋转状态。其阻力计算方法如下：

（1）计算水流冲刷作用下螺旋桨驱动轴系时的摩擦阻力矩，通常设定轴系摩擦力矩为定值。表达式为：

式中 Mf——与桨一起旋转的部分摩擦力矩，kN·m

Me——主机输出扭矩，kN·m

ηc——轴系传递效率

从公式中可见，摩擦力矩主要由轴系的传递效率决定。

（2）将KT和KQ曲线延长到负值范围，直到进速系数Jp值达到螺旋桨正常工况时进速值的1.5～2.0 倍。在KT和KQ都为负值的Jp范围内取一连串Jp值，并计算对应的Kd，形成直径—效率系数曲线。。

（4）计算进速系数Jp。

（5）按照公式，可得出在给定来流下自由旋转螺旋桨的转速。

（6）根据计算的Jp值计算对应的KT。

（7）根据得到的KT，计算螺旋桨自由旋转时所受阻力。Rp=KTρnm2D4。

随着进速Vp不断增加，自由旋转的螺旋桨达到临界状态时的转速nm也不断增加，旋转方向与工作螺旋桨一致。考虑尾部伴流的影响，非正常工况自由旋转螺旋桨内桨阻力值小于外桨。故在实际计算中，内桨阻力公式修正为Rp=K脱KTρnm2D4，其中，K脱是小于1 的修正系数。

1.3 船机桨模型

螺旋桨推力P=Kpρn2D4，螺旋桨的推力作用于船体推动船舶前进的部分称为有效推力Pe；另一部分用于克服附加阻力。Pe=（1-t）P=（1-t）KTρn2D4，其中，t=（P-Pe）/P，t 是推力减额系数。

船桨系统的运动方程：

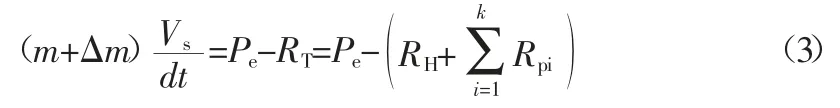
式中 m——船体质量

Δm——船舶附水质量，一般取值范围为（5%～15%）m

Vs——航速

RT——船体总阻力

RH——正常工况下船体阻力

Rp——非正常工况下桨的附加阻力

2 GUI 界面和数据库

为方便调试，在Matlab/Simulink 中搭建相应的仿真模型。船桨模型用户界面如图1 所示。采用Matlab/GUI 开发界面，可灵活设置船舶参数、螺旋桨参数和环境参数。

（1）船舶参数。包括排水体积、排水量、船体附水质量系数、额定船速、船长、船宽、吃水、方形系数、棱形系数、中剖面系数等。

（2）螺旋桨参数。包括桨的额定转速、直径、螺距比、盘面比、桨叶数、桨轴浸深等。

（3）环境参数。包括海水密度、空气密度、风压系数、风浪阻力幅值、风浪阻力周期、风向角、流向角等。

GUI 界面上还可设置船型、推进型式、海况、工况，并设置风浪流及恶劣海况等外部环境影响。仿真运行时，可选择是否实时显示仿真结果曲线；仿真结束后，可选择不同坐标参量显示仿真结果，并将之保存。软件具有编辑样本数据，保存样本修改历史，显示仿真结果来源等功能。

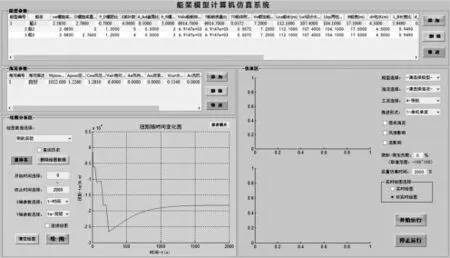
图1 船桨模型用户界面

3 典型工况实验

在GUI 界面输入某四机四桨船参数，海况设置为0 级，工作桨设置为2.2 r/s，进行锁轴和拖轴实验，实验结果见图2～图7。

3.1 四桨船锁轴仿真曲线

由图2 可知，双内桨锁轴时螺旋桨的阻力是平稳上升的，在到达3.1×105N 时，趋于稳定。由图3 可知，双外桨锁轴时螺旋桨的阻力是平稳上升的，在到达3.3×105N 时，趋于稳定。对比两图可知，外桨锁轴时外桨所受到的阻力值大于内桨锁轴时内桨所受到的阻力值。

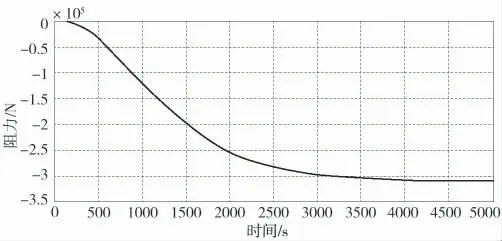
图2 双内桨锁轴时两内桨阻力曲线

图3 双外桨锁轴时两外桨阻力曲线

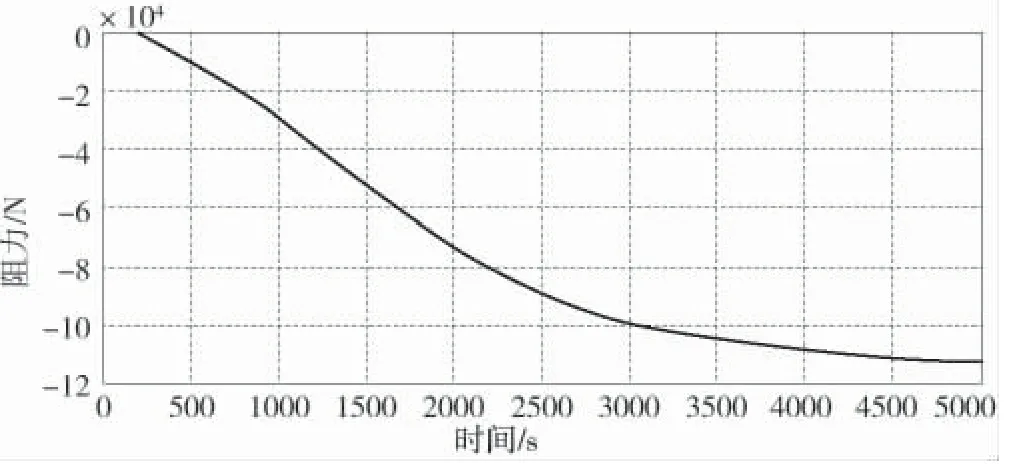
图4 双内桨脱轴时内桨阻力曲线

3.2 四桨船脱轴仿真曲线

图5 双外桨脱轴时外桨阻力曲线

由图4 可知，双内桨脱轴时螺旋桨的阻力是平稳上升的，在到达1.3×105N 时，趋于稳定。由图5 可知，双外桨脱轴时螺旋桨的阻力是平稳上升的，在到达1.2×105N 时趋于稳定。对比两图可知，内桨脱轴时外桨所受到的阻力值大于外桨脱轴时内桨所受到的阻力值。由图6 可知，螺旋桨的进速平稳上升，在到达10.77 m/s 时保持稳定。由图7 可知，螺旋桨的进速平稳上升，稳定在11.03 m/s。

根据仿真模拟实验结果可得出以下结论：

（1）锁轴阻力大于脱轴阻力。

（2）外桨脱轴时航速高于内桨脱轴时的航速。

（3）锁轴或脱轴情况下，外桨阻力值大于内桨阻力值。

4 结语

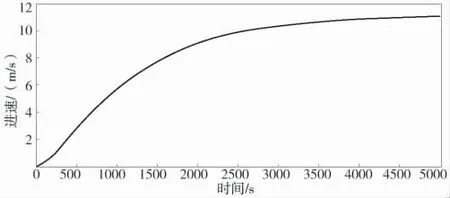
图7 双外桨脱轴时进速曲线

为了能对复杂工况下的船桨特性进行仿真，本文采用卡耳玛柯夫经验公式对螺旋桨阻力进行估算，并结合锁轴和脱轴工况对内桨阻力公式进行修正，最终得到船桨系统的运动方程。根据船桨的数学模型在Matlab/Simulink 中构建对应的仿真模型，开发GUI 界面，方便用户设置船型参数、螺旋桨参数和环境参数。针对某型船的典型工况仿真实验表明，船舶阻力和螺旋桨的负载特性都能得到较好模拟。后续工作中将收集更多的船型和桨型实船数据，进行计算与分析，以进一步验证本文开发的船桨仿真模型的普适性。