基于改进模糊层次分析法的设备维修方式决策

叶远龙

（歌尔股份有限公司，山东潍坊 261000）

0 引言

生产设备是工业生产中不可或缺的一部分，随着工业生产的现代化和高效化，生产设备在工业生产中将发挥越来越重要的作用。而设备的功能繁多使得其结构日益复杂，出现故障的概率也随之提升，维修也变得更加困难。根据不完全统计，生产型企业维修设备的费用最多可以占据所有生产费用的将近70%，且其中很多都是不必要的维修费用。由于生产设备的结构复杂，因此维修过程也变得更加不稳定，这也是不必要维修的费用增加的原因。因此有必要引入一种新的维修决策方式，提升故障检测和维修的效率。

1 工业生产设备的维修方式

目前通用的工业生产设备的维修方式有两种：一种是故障维修，另一种是预防性维修。故障维修是指设备发生故障后才进行的维修工作，其目的只是解决设备故障，因此本文不做讨论。

预防性维修是指设备未发生故障时，为提升设备运行的稳定性，对设备中的零部件进行维修，提升设备的稳定性，防止其出现故障。而生产设备的种类繁多，设备的结构也非常复杂，在设备未出现问题时很多情况下很难制定设备的维修方案，因此需要引入一套预判系统，对设备中的潜在问题进行针对性维修，降低维修的成本，提升企业的经济效益。

由于对设备的预防性维修属于典型的决策问题，即“应该维修什么部位”和“如何进行维修”，因此适用于使用模糊层次分析法进行决策。而传统的模糊层次分析法中是先计算全总后再进行一次性检验，一旦检验不通过需要重新进行计算，计算效率较低，不适用于大型生产设备较多的工业企业。本文引入最优决策矩阵对模糊层次分析法进行改进，提升其计算效率。

2 设备维修的决策模型和决策步骤

针对工业生产设备的属性，建立决策模型时，应当将其分为目标层（D）、准则层（C）和措施层（P）。以港口中常见的吊装设备为例，融合设备的停机时间、维修性、故障率、对环境的影响、对系统的影响、维修费用和设备停机造成的损失等因素作为决策模型建立的基础，建立的决策模型如图1 所示。

根据图1 的决策模型，当对某一特定的设备进行维修时，具体决策步骤如下：

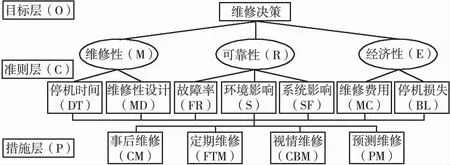
图1 维修方式决策模型

按照设备的结构和工作特性，首先将父准则层中的维修性（M）、可靠性（R）和经济性（E）进行比较，为其分配权重wm、wr和we，其次是对其下属的子准则层进行比较后分配权重，分配方式与父准则层相似。

准则层的权重分配完毕后，应当针对措施层进行权重分配。由于措施层中对应上部7 个准则层，因此每一措施层都有对应的7 个准则层的7 个权重，应当全部进行考虑，如措施事后维修（CM）对应7 个准则层分配的权重为。其他措施层的权重分配方式与之相似。

确定措施层对应的7 个准则层的权重后，计算各自的总体权重，4 个措施层中总体权重最大的就是将要采取的维修方式。如事后维修的总体权重计算方式为：

其他3 种维修方式的权重计算方式与式（1）类似。对于不同的设备，由于准则层中的相关数据不同，得出维修权重也不相同，即不同的设备应当采取不同的维修方式。

3 设备维修决策中模糊分析法的改进

由于工业生产设备的结构复杂，造成故障的原因非常多，因此单纯地计算权重容易造成较大的误差，为此需要在决策模型中引入专家评判矩阵。专家评判矩阵是一种通过专家评判确定一致性的矩阵，但在传统的评判方式中，如果专家评判矩阵的结果未能通过一致性检验，则应当重新进行评判，显得非常麻烦，当设备数量众多时也是不现实的。为此，引入了最优传递矩阵，对传统的专家评判矩阵的一致性判定方式进行改进，缩减评判的时间，提升评判的效率（图2）。

图2 改进后的判断和评估流程

由图2 的决策步骤可知，采用将模糊数对比模糊矩阵的方式得到相对于上一层或同层其他因素的权重。而本文选取的模糊数为三角模糊数，三角模糊数的应用范围较广，因此得到的数值相对较为准确。三角模糊数设定两个影响因素i 和j，并计算其模糊比较值aij，aij=（lij，mij，hij）。其中，l、m 和h 分别是模糊比较值aij的下限值、中间值和上限值。

在三角模糊数中，如果使用“1”表示同样重要，“2”表示稍微重要，“3”表示比较重要，则aij=（1，2，3），此时因素i 和因素j 同样重要或是i 比j 略微重要。则由三角模糊值构成的矩阵为：

其中，n 为矩阵中因素的数量。按照本文中选取的示例，n 应当取2。

按照矩阵中的上限值、中间值和下限值，矩阵A 还可以进一步拆分，拆分为，且由于aij＞0 和aij=1/aji，因此矩阵A 属于互反矩阵，因此可以得到矩阵A 的反对称矩阵B：

由此可知矩阵B 满足bij=-bji，这样可以得到矩阵B 的最优传递矩阵C：

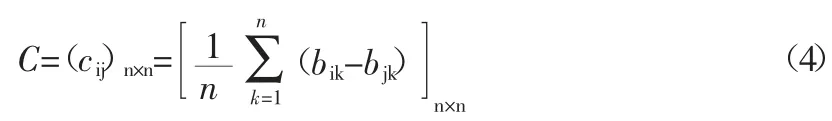
按照相似的方式，可以计算矩阵A 的最优传递矩阵A*：

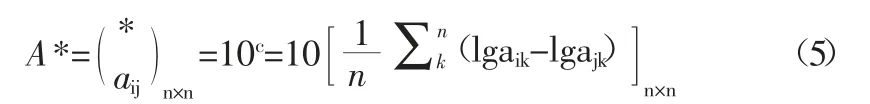
通过A*可知该矩阵本身就具有一致性，因此无需再进行繁琐的一致性检验，通过矩阵A*可以直接求出权重值，进而得出维修设备的最佳方案，提升计算和维修设备的效率。

4 决策因素权重的确定

在应用改进后的模糊层细分析法进行设备维修方案的权重判定时，需要注意三角模糊数中的上限值、中间值和下限值的问题。因此需要对参与设备维修的因素的重要性进行评价，从而建立三角模糊判断矩阵A，并应用式（5）对模糊判断矩阵A 进行一致性转化，最后采用平均求和的方式得出上限值、中间值和下限值所占据的权重，可以表示为。

5 实例分析

为衡量改进后的模糊层析分析法能否得出维修设备的最佳方案，以某港口中的吊装设备和运输设备为例，对该方法进行了检验。模糊层析分析法中的判断尺度则采用常见的1-9 标度法，具体定义见表1。

表1 判断尺度

首先针对机械设备进行准则层维修性（M）、可靠性（R）、经济性（E）之间两两比较，并得到三角模糊分析矩阵A：

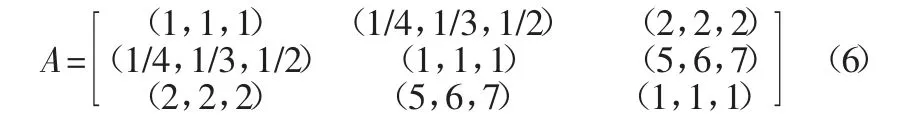
这样就可以得到准则层的权重向量为W（C）=（0.252 5，0.636 7，0.143 4），通过一致性矩阵的转换方法可以得到一致性参数为γ1=0.925 4。而通常的模糊分析方法中，一致性参数的范围为0.358 4＜γ＜1，因此得出的一致性参数在合理的范围内，可以用于计算设备维修过程中的权重值，进而得出设备的具体维修方案。

在上述的基础上，结合式（1）得到的4 种措施层的参数为W=（0.052 3，0.011 6，0.274 0，0.563 2），由此可以得出该设备的最佳维修方式是预测性维修（PM），即第四种。

6 结论

鉴于传统的决策矩阵的检验一致性的方法非常繁琐复杂，不适用于设备较多的生产企业，本文对改进的模糊层次分析法的设备维修方式决策进行了研究。本文改进了一致性检验的方式，通过具备一致性的矩阵A*求出权重值，可以无需繁琐的一致性检验，直接得出结果。通过实例分析后得知，该方式可以成为对设备维修进行决策的有效方案，结果较为精确，且计算的步骤较少，因此值得在设备较多的大型生产企业中推广应用。