真问题真探究真学习
2020-11-16陈瑶
陈瑶


一、真问题,让思考生长起来
问题是学习的重要组成部分,但当前的数学课堂上,问题多是教师提出的,鲜有学生的提问与质疑。“本真数学”则强化学生的提问。
以《三角形的三边关系》为例,教材提供了4组固定长度的纸条(⑴6、7、8;⑵4、5、9;⑶3、6、10;⑷8、11、11),要求学生在用纸条围三角形的过程中发现和归纳三角形三边的关系。学生尝试之后,提出问题:除了第⑴组可以围成三角形,其他三组为什么无法围成三角形?笔者提示:如果从任两边的和与第三条边比较考虑,会如何呢?学生仍不得要领。基于此,笔者开始思索:发现和提出问题绝不仅仅是学习的开始,它应该贯穿于学习的全过程。于是,笔者尝试创设“问题链”,以激发学生的持续思考。
问题1:怎样用一根吸管围成三角形?笔者让学生准备1根吸管、1把剪刀,引导学生思考“要围成一个三角形,这根吸管该怎样剪?”学生把它剪成三段。笔者接着提问:“我们剪好的3段可以分成几种不同的情况?”通过分类,学生发现无论怎样剪,三段吸管的长度关系无外乎三种情况:a+b
问题2:任意三段都能围成三角形吗?受材料和操作误差的影响,课堂往往会“卡”在“两段的长度之和等于第三段”时能否围成三角形。一名学生在投影仪上展示了他用a+b=c公式拼成的“三角形”。笔者没有回避错误,而是放大投影,让学生质疑。不一会儿,有学生质疑:“较短的两根纸条能接上吗?”“接头的点在哪儿?a和b拱得起来吗?”此时的课堂已非常活跃。笔者借助课件把这样的三段吸管抽象成三条线段(图1),让学生聚焦质疑点“当a+b=c时,三条线段能围成三角形吗?”借助多媒体的动态演示,学生发现a和b的两个端点无法重合,便立即理解了a+b=c时,三条线段不能围成三角形。
问题三:怎样的三条线段能围成三角形呢?研究至此,笔者指着屏幕上的这三条线段继续追问:“同学们认为怎样的三条线段才能围成三角形呢?”学生开始大胆想象:“只要将a或b延长那么一点点就行了。”
学生的思考在一个个生动的“问题链”中逐渐深入,为后面推理归纳“任意两边之和大于第三边”积累了直观经验。
二、真探究,让思维理性起来
数学是一种理性精神,在发展理性思维的过程中,需要秉持嚴谨的研究态度,运用科学的方法去探索和解决问题。
1.于猜想中培养大胆求证的精神
在执教综合与实践活动课《掷一掷》时,笔者设计了师生共同掷骰子的游戏。规则如下:如果掷到两个骰子之和等于5时,则学生得分;掷到其他数字时则老师得分。学生立即反对:“游戏规则对我们不公平。老师有5个数,我们只有1个数,老师获胜的可能性大。”笔者相机指出:“如果将2个骰子同时掷出,点数和可能是几?一共有多少种可能?”学生思考后回答:“点数和可能是2到12,一共11种,点数和分别是2、3、4、5、6、7、8、9、10、11、12。”笔者再次设计规则:把这11个数也分成两组,第一组是2、3、4、10、11、12,暂且定为蓝队;第二组是5、6、7、8、9,可以称之为红队。双方轮流掷2个骰子,掷出第一组数字,蓝队得分,掷出第二组数字,则红队得分。然后,笔者提问:“你们想加入哪个战队?为什么?”学生答“蓝队比红队多一个数,我觉得蓝队赢的可能性大”,还有学生答“我觉得5、6、7、8、9数字比较集中,红队赢的可能性大”。在学生做完游戏之后,笔者引导:“将各组掷到蓝队和红队的次数进行汇总,你发现了什么?”有学生答“我发现红队得分的次数多”,有学生答“5、6、7、8、9这些数出现的次数最多”。于是笔者又引导学生进行电脑模拟掷骰子试验,结果是红队获胜。笔者提问:“这是因为红队的运气好吗?”经过小组讨论,最终学生达成一致意见:2和12掷出的可能只有一种,而5、6、7、8、9掷出的可能不止一种。
从小组数据呈现到计算机随机大数据验证,学生真切感受到5、6、7、8、9出现的次数比较多,红队获胜的可能性比较大,他们已经迫不及待地想弄明白这样的现象背后究竟隐藏着怎样的数学奥秘,这正是数学习应具备的大胆求证精神。
2.于表征中培养自主创造的能力
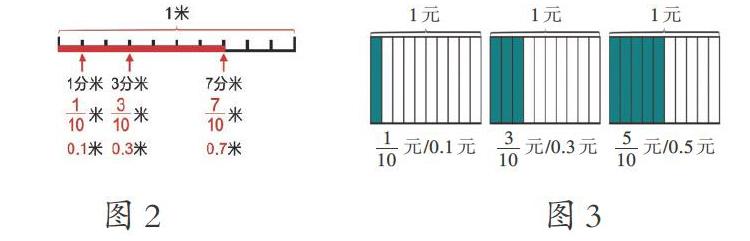
在《小数的初步认识》教学中,笔者引入多维表征,打通知识间的联系,深化概念的理解、构建多维度的学习链接,较好地培养了学生的创造力。
三、真学习,让素养丰厚起来
六年级上册《数学广角——数与形》中的例2[12+14+18+116+132+164+…=]是一个无穷递缩等比数列的求和问题。因为是无穷项累加求和,涉及极限,而极限思想是用无限逼近的方式来研究数量的变化趋势,对学生来说非常抽象。
学生借助所学,用圆、线段、正方形等基本几何图形直观地描述出了算式的内容(图5)。有学生认为如果继续“分割”下去,图中好像总有“剩余部分”,算式的结果应该比1小;还有学生感觉结果应该等于1。
学生虽然没有看出答案,但借助直观图已经看出了图形的变化趋势,隐约感觉该算式的结果应该与“1”有关。于是,笔者引导学生想象:如果无限加下去,空白部分就越来越小,和就越来越接近于1,当加数的个数无限多时,颜色将整个图形涂满,和就是1。
基于经验自主构图展开研究,借助有限图形展开想象,从变化趋势中推想出无限结果,既体现了创新意识,也促进了学习能力的发展,显示出数学素养聚合的强大能量。
(作者单位:武汉市汉口辅仁小学)
责任编辑 吴锋
