滚筒分选机内肥料运动特性的仿真与试验
2020-11-16宋学锋孙耀恒张方圆张锋伟赵武云
宋学锋 戴 飞* 孙耀恒 张方圆 张锋伟 赵武云
(1.甘肃农业大学 机电工程学院,兰州 730070;2.白银矿冶职业技术学院 机电工程系,甘肃 白银 730900)
肥料是农业生产的重要物质基础,肥料品质直接影响农作物的生长状况。在肥料造粒过程中,大颗粒肥料营养元素含量较多,而小颗粒及破损肥料的营养元素含量不足,影响田间生产中肥料的利用率[1]。因此,一方面在生产过程中要对肥料颗粒进行分选,收集破损及杂质颗粒,再将破损的颗粒及小颗粒肥料进行二次加工;另一方面在田间施肥前,要分选小颗粒及破损肥料,保证肥料颗粒尺寸相近、营养元素含量相当,以此避免地块施肥不均的情况发生。这样从肥料生产品质和施肥均匀性2方面可以提高肥料利用率,从而为逐步打造精准变量施肥农业及可持续发展农业生产[2-3]提供保障。
目前,肥料分选设备按筛分原理不同可分为振动筛、摇摆筛及滚筒筛3种。振动筛扬尘较大,筛网堵塞频繁、磨损快;摇摆筛适用于粉末与颗粒状混合物,噪音小,筛网寿命长;滚筒筛则驱动方式简单,占地面积和扬尘小,运转平稳[4]。本研究使用的滚筒分选机是采用回转驱动方式的一种分选设备,常用于肥料、种子等农业物料的分选作业,针对这种设备国内已有相应的研究。安进[5]从物料受力及运动角度对影响滚筒分选质量的因素进行分析表明,袋孔的形状、尺寸和分布密度是影响分选质量的显著因素。李寒松[6]对国内外不同分选方式的设备发展现状进行了对比分析,指出我国在分选设备的大型化、智能化及规模化发展上还需进一步加大研发力度。吴明亮等[7]针对设计的水稻窝眼滚筒分选机进行了运动及结构参数研究,得到分选效果最优的设备工作参数(滚筒外径、转速、窝眼孔径、孔深)。张林海等[8]对滚筒筛分机中农作物秸秆含有金属、塑料织物、砂石等杂质时的分离性能进行了研究,试验获得了物料筛分过程中滚筒工作时合理的转速和倾角范围。可以看出,已有研究主要集中在设备性能优化、谷物及秸秆分选等方面,对肥料分选及滚筒内物料运动规律分析较少。本研究拟采用DEM模拟法对肥料整粒及破损颗粒在滚筒分选机内的运动过程进行仿真分析,探究整粒与破损肥料颗粒数量变化,破损肥料颗粒位置变化及极限脱离角大小,并进行试验研究,旨在为肥料滚筒分选机的结构优化提供一定的理论参考。
1 计算模型建立
1.1 滚筒分选机模型
滚筒分选机是一种按颗粒长度和形状不同从整粒物料中分离破损颗粒及杂质的设备,由收集槽、螺旋输送器、滚筒等主要部件构成。滚筒中心位置安装着收集槽及螺旋输送器,图1为肥料滚筒分选机模型及窝眼剖面图。其中筒长200 mm,底面半径150 mm。窝眼位于滚筒内壁,为圆柱状结构,直径3.0 mm,深2.0 mm,出口做半径为0.5 mm的圆角处理(图1(b))。窝眼单排19个,相邻2窝眼轴向中心距10 mm。工作时筒的转速为30 r/min,螺旋输送器转速80 r/min。肥料加入滚筒后随着滚筒的旋转做回转运动,小粒径肥料在运动过程中会进入窝眼,随滚筒的转动被提升至一定高度,最后脱离窝眼落入收集槽,由螺旋输送器排出设备,从而实现与整粒物料的分选。
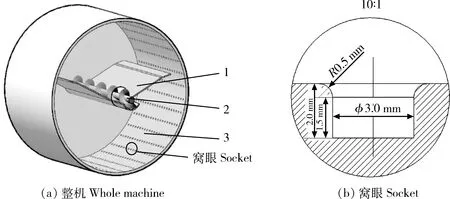
1.收集槽;2.螺旋输送器;3.滚筒1.Collecting tank; 2.Screw conveyor; 3.Drum图1 肥料滚筒分选机模型及窝眼剖面图Fig.1 Fertilizer drum separator model and socket section view
1.2 肥料模型
在农业生产中,肥料形态以散体颗粒为主,球形率在90%以上[9-10]。本研究借助EDEM软件建立肥料颗粒离散元模型,直径统一设置为3.0 mm,破损肥料则采用多球面聚合法组成长2.5 mm、宽2.2 mm、高2.0 mm的不规则颗粒[11-12]。离散元模型见图2。

图2 肥料颗粒离散元模型Fig.2 Discrete element model of fertilizer particle
2 数学模型
2.1 仿真中固相控制方程
在离散元理论中,颗粒的直线运动和旋转运动遵守牛顿第二定律[13-14]。计算前首先判断颗粒与颗粒、颗粒与壁面的接触情况,接着由牛顿第二定律可得颗粒间作用力变化,再由力的变化得颗粒位移变化。最后通过不断迭代计算确定整个颗粒群的状态[15-16]。颗粒运动控制方程如下:
(1)
(2)
式中:mi为颗粒质量,kg;t为计算时间,s;vi为颗粒速度,m/s;fi为作用在颗粒上的力,N;Ii为颗粒转动惯量,kg·m2;ωi为颗粒角速度,rad/s;Mi为作用在颗粒上的力矩,N/m。下标i表示不同的颗粒。
2.2 滚筒中颗粒运动动力学分析
滚筒在转动过程中,速度太快容易导致物料受到过大的离心力而不能从窝眼中掉落,速度太慢又不能保证物料提升到一定高度。合理的旋转速度才能使进入窝眼的破损肥料分离。物料在上升过程中主要受重力、摩擦力、离心力(图3),将重力G分解为沿切向轴x-x'的Gsinβ和沿法向轴y-y'的Gcosβ的2个力。摩擦力Fn则由离心力Fc与Gcosβ的合力提供。临界状态即为滚筒转速nmax最大时颗粒向上运动与向下运动的力达到平衡状态,可由式(3)[17]计算:
Gsinβ=f(Gcosβ+Fc)
(3)
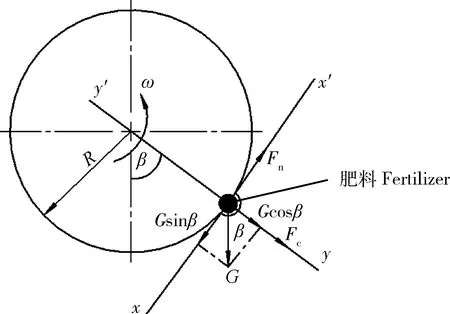
ω为肥料运动角速度,rad/s;R为滚筒半径,mm;β为肥料脱离角,(°);Fn为摩擦力,N;Fc为离心力,N;G为肥料重力,N;Gsinβ和Gcosβ分别为重力G在切向轴x-x'和法向轴y-y'上的分力,N。ω is the angular velocity of fertilizer, rad/s; R is the radius of drum, mm; β is the escape angle of fertilizer, (°); Fn is the friction force, N; Fc is the centrifugal force, N; G is the gravity of fertilizer, N; Gsinβ and Gcosβ are the component of gravity in the tangential axis x-x′ and the normal axis y-y′, respectively, N.图3 肥料滚筒分选机内肥料颗粒受力分析Fig.3 Force analysis of fertilizer in fertilizer drum separator
式中:G为肥料重力,N;β为物料的脱离角,(°);f为料与滚筒壁面摩擦因数;Fc为离心力,N。此时,离心力为:
(4)
式中:m为肥料质量,kg;R为滚筒半径,m;vn为肥料运动的线速度,m/s;n为滚筒转速,r/min。联合式(3)、(4)得:
(5)
根据式(5)可得该滚筒分选机最大转速nmax=77.5 r/min,所以本研究中设置滚筒转速为30 r/min是合理的。
3 参数设置
仿真中生成整粒肥料颗粒10万个,破损肥料颗粒2万个。仿真共进行50 s,时间步长1.4×10-5s。肥料颗粒的物理参数及接触参数较完备,已有大量与肥料相关的仿真研究。因此,本研究参考现有的肥料物性参数,具体数值见表1[18-19]。
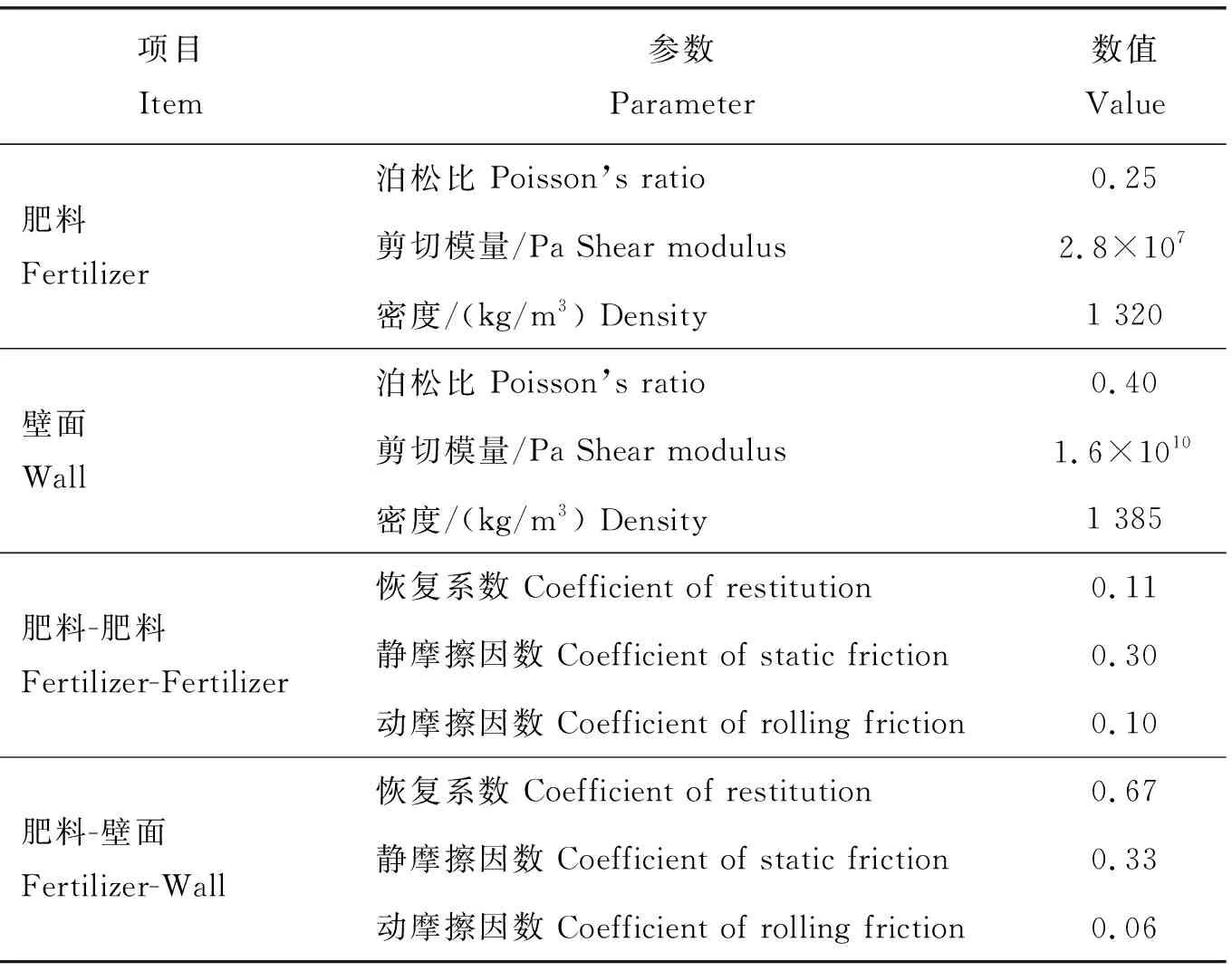
表1 EDEM中肥料属性及接触参数Table 1 Parameters of fertilizer and contact in EDEM
4 结果与分析
滚筒在启动后肥料颗粒由静止变为运动状态,波动较大,为避免分析中带入干扰因素,在肥料颗粒达到稳定状态(t=3.7 s)后进行相关数据统计。
4.1 整粒与破损肥料颗粒数量变化
图4为不同区域内肥料颗粒的速度云图。可以看出,肥料颗粒根据速度不同发生了分层现象,筒内颗粒可分为3个区域,分别为自由层、交接层、迟滞层[20-21]。自由层为颗粒快速流动区域,在滚筒内颗粒运动达到稳定状态后,该区域颗粒受自身重力会发生快速流动,颗粒群做雪崩式的抛落运动,颗粒的速度方向沿自由流动表面指向滚筒底部。交接层内颗粒分布在自由层附近时,颗粒速度方向与自由层内颗粒保持相同。而分布在迟滞层附近时,颗粒速度方向则与迟滞层内颗粒相同。同时,分布在该区域中心位置的颗粒位移变化比整体区域其他颗粒小,颗粒绕区域中心位置发生回转运动。迟滞层颗粒主要受到滚筒壁面带动及颗粒间剪切作用,沿壁面向上运动,速度方向与自由层内颗粒相反。由以上分析可以得出,自由层与迟滞层内颗粒运动速度较高,发生的位移变化较大。实际分选作业中破损肥料集中在这2个区域内时,在不断的回转运动过程中便能与窝眼有更多的接触几率,从而被分选出来。

图4 不同区域内肥料颗粒的速度云图Fig.4 Velocity map of fertilizer particles in different areas
对筒内颗粒数量进行统计,整粒肥料由于粒径较大,不能完全进入窝眼中,但个别颗粒会陷入窝眼口,随着滚筒的旋转而被带入收集槽。从统计数据可以看出,经过t=50 s的仿真,系统内整粒肥料共被带出22个(图5(a)),而破损肥料颗粒在整个仿真中共被带出1 600个(图5(b))。

图5 肥料滚筒分选机内肥料数量随时间的变化Fig.5 Fertilizer quantity change with time in fertilizer drum separator
4.2 破损肥料颗粒位置变化
滚筒旋转过程中肥料颗粒位置会发生不断变化,为便于统计肥料颗粒在不同时刻的空间分布,将滚筒空间划分为5个不同位置的统计区域(图6)。每个统计区域由200个矩形单元(20 mm×14 mm×10 mm)构成,自图6(b)中模型左端面开始沿x轴坐标依次为10、50、100、150、190 mm。矩形单元内的肥料颗粒在不同时刻的速度、角速度、位移、数量等物理量都将被记录,这样便可快速分析出肥料颗粒在滚筒旋转过程中的运动规律。
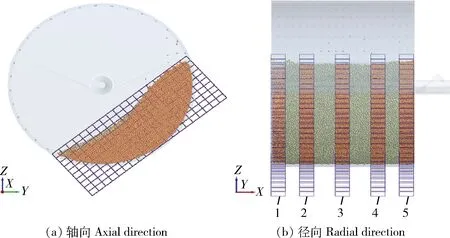
1,2,…,5分别为x=10、50、100、150、190 mm处的统计区域。1, 2, …, 5 are statistical areas at x=10, 50, 100, 150, 190 mm respectively.图6 肥料滚筒分选机内不同位置的统计区域Fig.6 Statistical area distribution of different positions in fertilizer drum separator
分别提取每个矩形单元内破损肥料颗粒在仿真时间t=3.7、30.0、50.0 s时刻分布数据,做出x轴向5种不同深度的破损肥料颗粒体积云图(图7)。可以看出:在初始时刻t=3.7 s,破损肥料基本均匀分布在滚筒中,以100 mm处的统计网络为对称位置(图7(g)),50和150 mm处((d)和(j))的颗粒体积含量基本相同,10和190 mm处((a)、(m))颗粒体积含量基本相同。随着滚筒的转动,t=30.0 s时,10和190 mm处((b)、(n))颗粒体积相对于t=3.7 s时((a)、(m))降低,50和150 mm处((e)、(k))颗粒体积相对于t=3.7 s时((d)、(j))增大,100 mm处((h))颗粒体积相对于t=3.7 s时((g))增大;t=50.0 s时,10 和190 mm处((c)、(o))颗粒体积相对于t=30.0 s时((b)、(n))进一步降低。50和150 mm处((f)和(l))中心位置相对t=30.0 s时((e)、(k))颗粒体积含量降低。由此说明,破损肥料颗粒随滚筒旋转过程中发生了轴向偏析,由滚筒两端向轴向几何中心位置集中。同时,靠近滚筒底部的肥料颗粒逐步聚集,这有助于破损肥料颗粒在运动过程中进入窝眼,提高肥料颗粒分选效率。
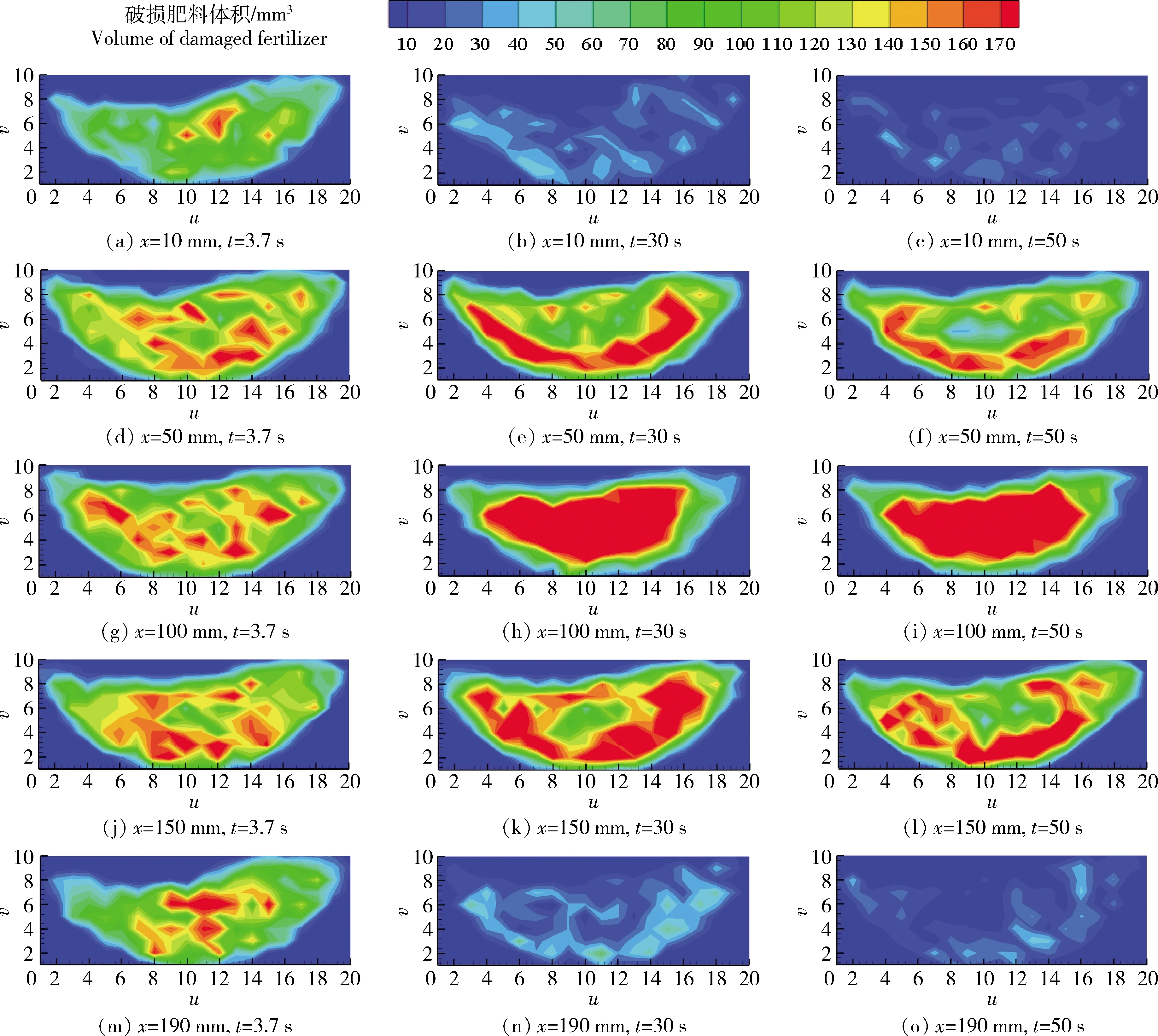
u、v分别为图6(a)中模型轴向视角统计区域的长、短直角边,数值为统计网格数量。x为图6(b)中模型左端面开始的轴向距离;t为仿真时间。u and v are the long and short right angle sides of the model axial view in Fig.6 (a), respectively.The values are the number of statistical grids; x is the axial distance from the left end face of Fig.6 (b); t is the simulation time.图7 不同位置和时刻的破损肥料颗粒体积云图Fig.7 Volume map of damaged fertilizer at different positions and times
4.3 破损肥料颗粒极限脱离角大小
肥料颗粒随着滚筒转动被提升,在脱离窝眼时获得一个水平方向速度并做抛物线运动,该速度大小影响肥料脱离窝眼后水平前进距离,脱离窝眼时的水平速度vh由式(6)计算:
(6)
可以看出,脱离角β越大肥料颗粒脱离窝眼时水平速度越大,越容易进入收集槽。对仿真中2处极限脱离位置的破损肥料的坐标进行提取,分别记为A(101.2、121.6、77.7 mm)、B(90.9、98.8、106.2 mm),测量得对应的脱离角分别为32.5°、47.1°。肥料颗粒自由下落时间为:
(7)
式中:T为下落时间,s;H为A、B两点的z坐标值,mm。将已知数据代入式(6)、(7),得2颗粒的水平运动距离分别为SA=33 mm,SB=52 mm。与收集槽边缘距滚筒内壁水平距离L(29 mm)进行比较可知,SA>L,L 对肥料在滚筒分选机中运动过程进行试验验证,研究对象选用芭田股份公司生产的复合肥料,试验台架包括变频器、减速电机、联轴器及滚筒等部件(图8)。肥料颗粒在流动时难以用现有设备观测并记录内部的位移变化,但分选过程中得到的破损肥料数量和脱离角容易记录。 1.支撑轮;2.变频器;3.电机;4.联轴器;5.轴;6.滚筒;7. 收集槽;8.相机1.Support of wheel; 2.Frequency converter; 3.Motor; 4.Coupling; 5.Shaft; 6.Drum; 7.Collection tank; 8.Camera图8 肥料滚筒分选试验台Fig.8 Test bench of fertilizer drum separator 试验前分别使用直径3.0和2.5 mm的圆孔筛对复合肥料进行筛分,得到符合要求的整粒肥料及破损肥料颗粒,数量分别为10万和2万个。将肥料颗粒加入滚筒后,调节变频器使电机输出转速为 30 r/min,待肥料颗粒达到稳定运动状态后开始收集被分选的颗粒,同时在滚筒端面处做视频记录,试验时间共50 s。因试验时间相对较短,落入收集槽的肥料颗粒较少,不会造成溢出,所以试验中未加螺旋输送器。 结果显示,落入收集槽的整粒肥料为20个,破损肥料为1 553个。与仿真结果进行对比,整粒肥料数量误差为9%,破损肥料数量误差为2%。由视频回放可测得破损肥料最小脱离角为30°,最大脱离角为45°。与仿真结果进行对比,最小脱离角误差为7.7%,最大脱离角误差为4.5%。试验数据误差均小于10%,在可接受范围,证明采用离散元法分析肥料颗粒在滚筒分选机中的运动是可行的。 1)本研究基于离散元法建立了整粒肥料与破损肥料颗粒模型,并对滚筒分选机内肥料运动过程进行仿真分析。滚筒内肥料颗粒在达到稳定运动状态时发生了分层现象,可分为自由层、交接层及迟滞层。自由层内颗粒以雪崩式流动为主,交接层内颗粒绕区域中心位置发生回转运动,迟滞层内颗粒则紧贴壁面被提升。 2)沿滚筒轴向划分统计区域对破损肥料颗粒分布位置进行分析,发现破损肥料颗粒在运动过程中发生了轴向偏析,由滚筒两端向轴向几何中心聚集;交接层内破损肥料逐步向自由层及迟滞层内聚集。这些运动规律有利于提高肥料颗粒分选效率。 3)破损肥料颗粒脱离角最大为47.1°,最小32.5°。破损肥料脱离窝眼后均能落入收集槽。 4)由试验结果可知,收集槽内整粒与破损肥料数量、最小脱离角与最大脱离角分别与仿真数据进行对比,误差<10%,证明采用离散元法研究滚筒分选机内肥料运动是可行的。 本研究基于试验台架开展,受试验观测手段的限制,研究中涉及的试验过程并不能完全等同于实际生产作业。但采用仿真方法得到的结果能从理论上对肥料颗粒在滚筒内的运动规律进行解释,仿真中产生的肥料颗粒运动规律与台架试验的表观现象相符合,证明采用该方法研究滚筒内肥料颗粒分选过程是可行的。后续还需进一步对影响分选效率的多种因素进行探究。5 试验验证

6 结 论
