Babbage 方程解的进一步讨论
2020-11-16余志恒
刘 娜, 李 松, 余志恒
(1.成都工贸职业技术学院通识教育学院,四川成都611731; 2.西南交通大学茅以升学院,四川成都611756;3.西南交通大学数学学院,四川成都611756)
早在百年以前,Babbage[1-2]、Abel[3]等就开始了迭代根的研究.随着动力系统理论的深入发展,多年来这一课题一直被人们广泛关注.设φ:E→E是集合X到自身的一个映射,称φ是一个已知映射F:E→E的n次迭代根,如果φ和F满足函数方程

例如,φ(x):=x2+2 是 F(x):= x4+4x2+6 的二次迭代根.
广义的说,迭代根事实上是一种特殊的迭代,即分数次迭代.由于它涉及到嵌入流问题,映射迭代根的研究更加引人入胜.1950 年,Isaacs[4]完成了一个奠基性的工作,即给出了抽象集上自映射的迭代根存在的充分必要条件.关于复函数,在Koenigs[5]局部结果的基础上,1950年,Kneser[6]做出了整函数ez的二次迭代根的全局结果,之后Rice等[7]对复函数做了进一步的结果.关于实函数,1968年及1990年,Kuczma等出版了他的专著[8 -9],系统的介绍了单变量函数方程,其中不仅研究了满足某些特殊方程的函数类,还对区间上严格单调连续函数的迭代根给出了一些很好的结果.关于迭代根的更多进展,可以参考文献[10-15].
特别的,如果F:=id,(1)式被称作Babbage方程[1],是由 Babbage 在 1815 年第一次提出来的,他告诉我们对于Babbage 方程的任意解φ,存在可逆函数h,使得与φ拓扑共轭的函数h-1οφοh亦为方程(1)的解.1916 年,Ritt[16]讨论了 Babbage 方程的一类实连续解,并对其进行了分类.1980 年,McCarthy[17]得出了Babbage方程在迭代次数为奇数时无非平凡的连续解,而迭代次数为偶数时,其连续解必定是迭代次数为2 时方程的连续解的结论,此外,他还举例讨论了Babbage 方程的不连续解.更多针对一维Babbage 方程可微解、解析解的问题,可以参考文献[18 -20].
本文在 McCarthy[17]工作的基础上,利用多项式代数理论并借助多项式代数系统Singular软件[21]进一步讨论了一维Babbage 方程的一类不连续解.此外,本文的主要部分研究了平面Babbage 方程的多项式解.将首先给出平面二次Babbage 方程的二次多项式解,并进一步证明该二次多项式解亦为n次Babbage 方程的解.最后,举例验证文中主要结果的正确性.
1 预备知识
本文主要讨论的是一维Babbage 方程的一类不连续解以及平面Babbage 方程多项式解的存在性问题.最终将其转化为考虑其所对应的代数簇是否非空的问题,即由一维Babbage 方程和平面Babbage方程所导出的多项式代数系统是否有解的问题,并且如果有解,有多少解,又如何求出并表示它的所有解.下面介绍代数簇和不可约分解的基本理论.
通俗地讲,代数几何学上的代数簇是多项式集合的公共零点解的集合.代数簇是经典(某种程度上也是现代)代数几何的中心研究对象.
定义 1[22-24]设 K 是一个域并且 f1,f2,…,f s是环 K[x1,x2,…,xn]中的有限多个多项式.由多项式f1,f2,…,fs所定义的仿射代数簇(简称为代数簇)是如下集合
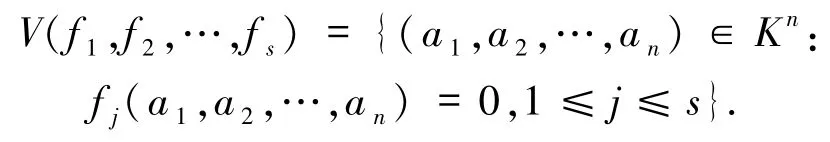
由以上定义可知,一个代数簇即为Kn的一个子集V,并且这个集合满足:存在有限个多项式,使得 V = V(f1,f2,…,fs).换句话说,代数簇 V(f1,f2,…,fs)⊂Kn就是Kn
中的包含有限个多项式方程的系统
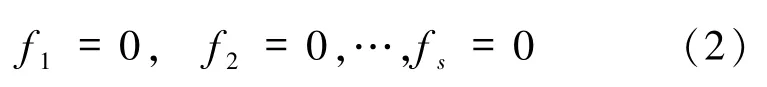
的解的集合.当然,这个集合依赖于域Kn,例如,如果取 K =R,那么 V(x2+y2+1)=Ø,但是取 K =C则不然.另外,不论取K为什么数域,V(x2+y2+1,x,y)=Ø.
令 F:= {f1,f2,…,fs},并将系统(2)简记为F =0.易知 V(F)= V(〈F〉).设理想〈F〉的 Gröbner基[22-24]为 G,由文献[23]定理 1 知道〈F〉= 〈G〉,进一步,有 V(〈F〉)=V(〈G〉).因此,F =0 的解集由多项式集合F所生成的理想唯一确定,它的研究可以转化为相应理想的 Gröbner 基的研究.根据Hilbert 弱零点定理(参见文献[23]的定理1.3.10),F =0 无解当且仅当 1∈〈F〉.可以通过计算 F =0 的约化 Gröbner 基来判断 1∈〈F〉是否成立,并进一步判断F =0 是否有解.事实上,通过计算约化Gröbner基,总可以判定一个多项式代数系统是否有有限个解,并在解的个数有限的情况下将其全部表示出来.这就需要进一步考虑代数簇的不可约分解.
在介绍代数簇分解的相关理论之前,首先讨论这样一个例子.考虑理想 I = 〈x3y3,x2y2〉,显然,它的代数簇V:=V(I)是另外2 个代数簇的并集,即V = V1∪V2,其中,V1是平面 x = 0,V2是直线{(x,y,z):y =0,z =0}.从几何的角度,可以清楚的看到V1和V2不能再分解为更小的代数簇的并,这里把V =V1∪V2称作不可约代数簇.
定义2[22-24]非空代数簇V⊂Kn被称作是不可约的,如果对于另外两个代数簇 V1和 V2,V =V1∪V2,仅当 V1= V 或 V2= V 时成立.
如前文所述任意理想〈xpyq,xrys〉,p,q,r,s∈N的代数簇是一个平面和一条直线的并集.一个自然的问题是:是否每一个代数簇都可以分解为一些不可约代数簇的并集?下面的引理给出了肯定的答案.
引理 1[23]令 V⊂Kn是一个代数簇.则 V 是有限多个不可约代数簇的并集.
由引理1,对任意代数簇V⊂Kn,存在有限个不可约代数簇 V1,V2,…,Vm⊂Kn,使得 V = V1∪V2∪…∪Vm.特别地,若对任意 i≠j 都有 Vi⊈Vj,则称V1∪V2∪…∪Vm为V的极小不可约分解.
引理 2[22,25]每个代数簇 V⊂Kn都有一个极小不可约分解

若不计Vj的次序,这个分解是唯一的.
对于域 K 的特征为 0 时,1988 年,Gianni等[26]给出了第一个关于代数簇极小不可约分解的有效的可执行算法.1996 年,Shimoyama 等[27]提出了一种由Gröbner基理论实现的算法.这些算法均可在计算机代数系统Maple和Singular中实现.
2 一维情形
文献[17]对一维Babbage 方程的连续解给出了完整的讨论,并在文章的最后举例说明一维Babbage方程存在不连续解.本节将讨论Babbage 方程的一类不连续解,即有理函数解.从分式线性函数开始,经过简单的计算有如下结果:
定理 1设其中 a,b,c,d∈C,a2+b2≠0,c2+d2≠0,a2+c2≠0,b2+d2≠0,b2+c2≠0,(ax+b,cx+d)=1,则
(i)f2= id 当且仅当 a =d =0,bc≠0;
(ii)f3= id 当且仅当 a2+bc +ad +d2= 0,bc(bc-ad)≠0;
(iii)f4= id 当且仅当 a2+ 2bc + d2= 0,bc(bc-ad)≠0 或 a = -d,bc-ad≠0.
证明经过简单的计算易得结论(i).关于结论(ii),计算 f3可得
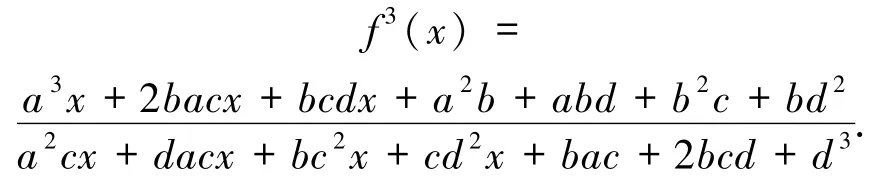
令 f3(x)=x,得出代数系统 F:={f1,f2,f3},其中
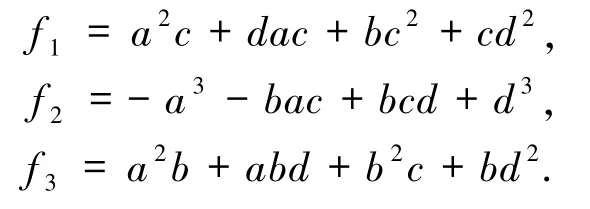
运用Singular的库primdec.lib中的命令minAssGTZ计算F 的代数簇的极小不可约分解,并由此获得Babbage方程f3=id存在分式线性函数解的条件:
1)b = c = a-d = 0;
2)a2+bc+ad+d2=0.
由条件 1)可得 f(x)= x 与 b2+c2≠0 矛盾,故f3=id 当且仅当 a2+bc +ad +d2=0,bc(bc -ad)≠0.同理易证结论(iii).定理证毕.
注1定理1 的证明方法可推广到Babbage方程迭代次数n≥5 的情形.此外,还可运用上述方法找出Babbage方程的一般有理函数解,即形如
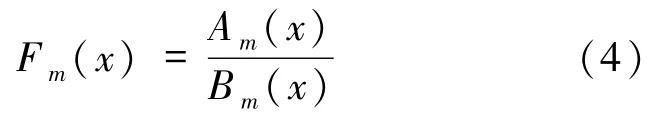
的解,其中
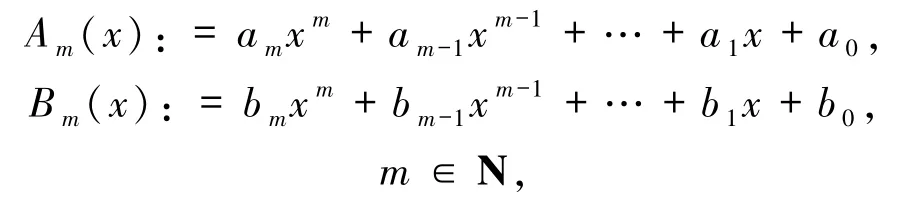
即所有正整数的集合,并且 ai,bi∈C,i = 0,1,…,m,使得以及(Am(x),Bm(x))=1.以 m =2 为例,运用定理 1 的证明方法,可得如下结论.
定理2Babbage方程f2=id存在形如
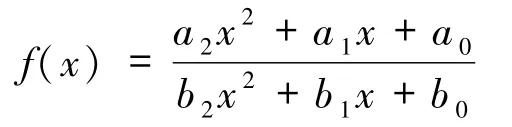
的解,并且满足(4)式中系数条件要求,当且仅当下述条件之一成立:
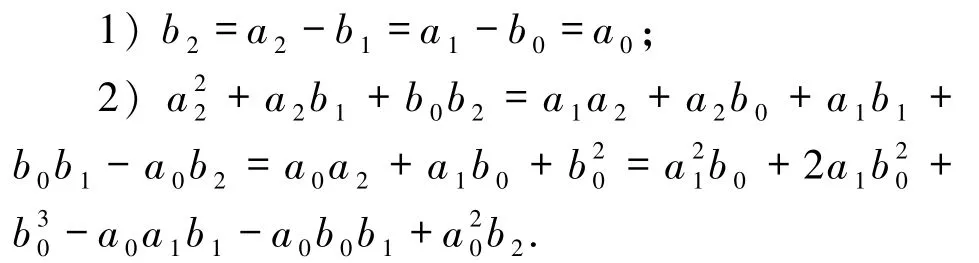
事实上,定理1 的证明方法可以找出Babbage 方程中迭代次数≥3 的情形其有理函数解.
3 二维情形
对于平面线性多项式映射
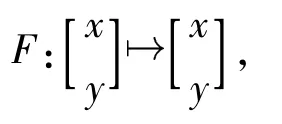
以及平面二次多项式映射
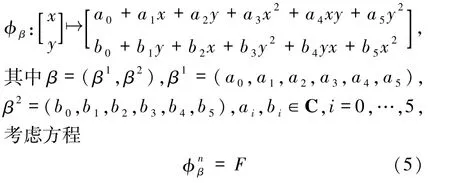
的解.针对方程(5),寻找其形如φβ的解实际上就是找出ai和bi最简代数关系,使得φβ的n次迭代恰好等于F.实际上,为了找寻ai和bi最简代数关系,利用多项式代数理论[21,24],有如下算法:
输入:平面多项式映射φβ和F.
输出:关于多项式φβ系数ai和bi的最简代数条件,使得(5)式成立.
过程如下:
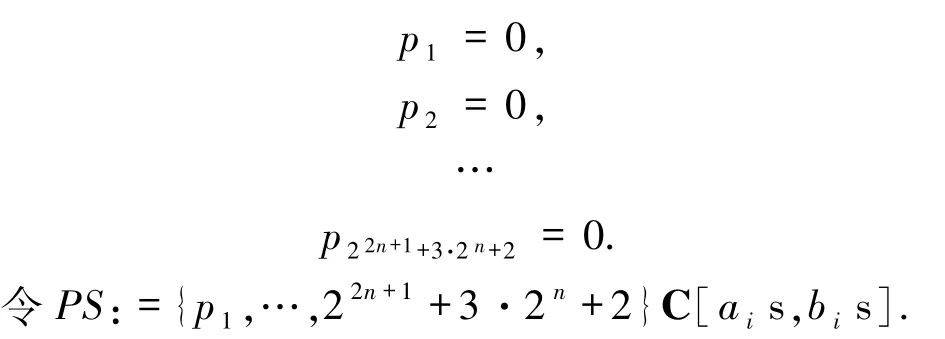
步骤 2 设定项序为分次字典序,变元序为ai> bi,计算 PS 的 Gröbner 基 G,若 G = {1},则输出:函数方程(5)无平面二次多项式解;否则,转步骤3.
步骤 3 设定项序为分次字典序,变元序为ai>bi,计算 PS 的 Gröbner基 G,若 G = {0},由 Hilbert弱零点定理[21,28],运用 Singular 的库 primdec.lib中的命令minAssGTZ 计算PS′的代数簇的极小不可约分解,并由此获得函数方程(5)有多项式解关于多项式φβ系数ai和bi的最简代数条件.
步骤4 将步骤3 中获得的条件重新带入函数方程(5),并判定由这些条件所确定的φβ是否为Babbage方程的解,以确定是否由增根,最终找出平面Babbage方程的平面二次多项式解.
作为上述算法的应用,我们讨论当n =2 时,Babbage方程(5)的平面二次多项式解有:
定理 3当n =2 时,方程(5)存在平面二次多项式解,当且仅当下列条件之一成立:
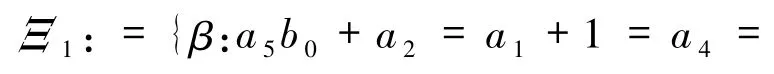
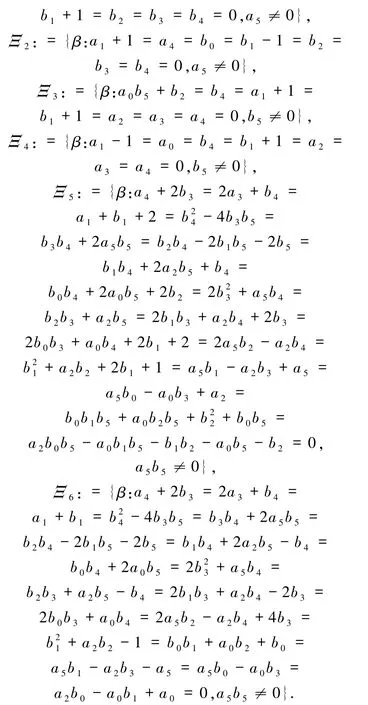
证明运用上述算法的步骤1,设φβ是方程(5)的一个二次迭代根,计算的二次迭代并令= F,比较和F 的系数,得到如下代数系统(记为 APS):
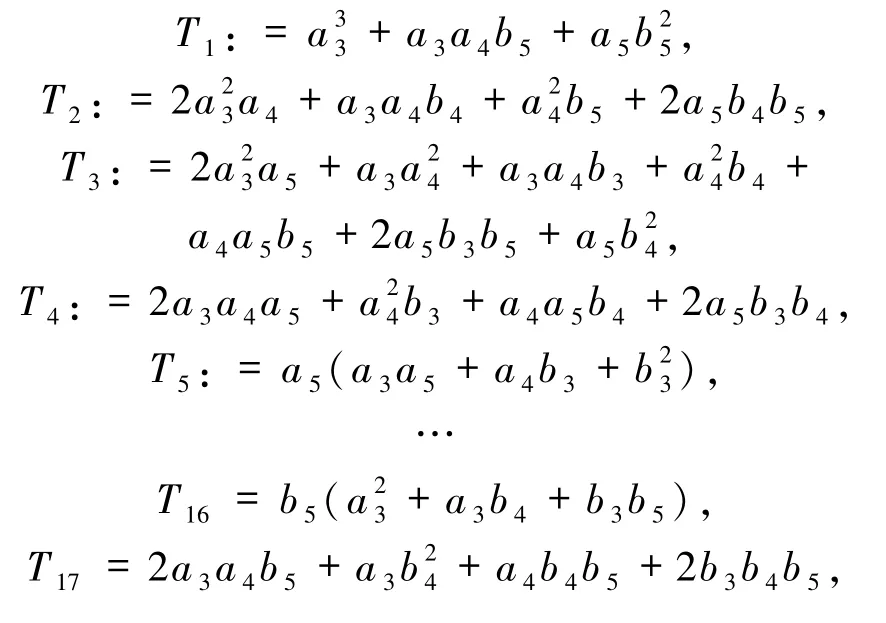
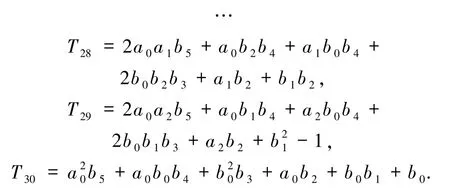
考虑到φβ是平面二次多项式,并结合T5和T16的形式,将代数系统APS分为如下3 个半代数系统
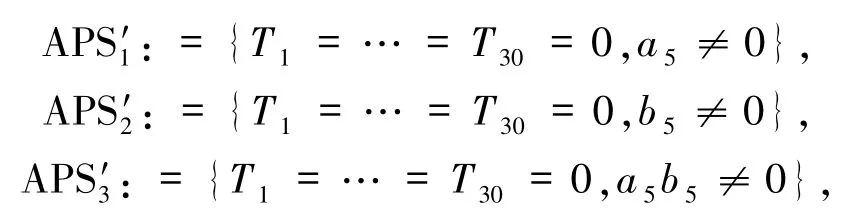
其中,3 个半代数系统中的每个多项式均为有理数域Q中的不可约多项式.为了避免冗余,仅针对半代数系统进行讨论,其他2 种情形可类似证明.
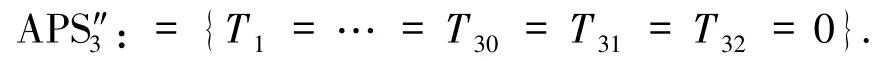
根据算法的步骤2 和3,设定项序为分次字典序,变元序为v >w >ai>bi,计算出的Gröbner 基G:={g1,…,g70},其中,
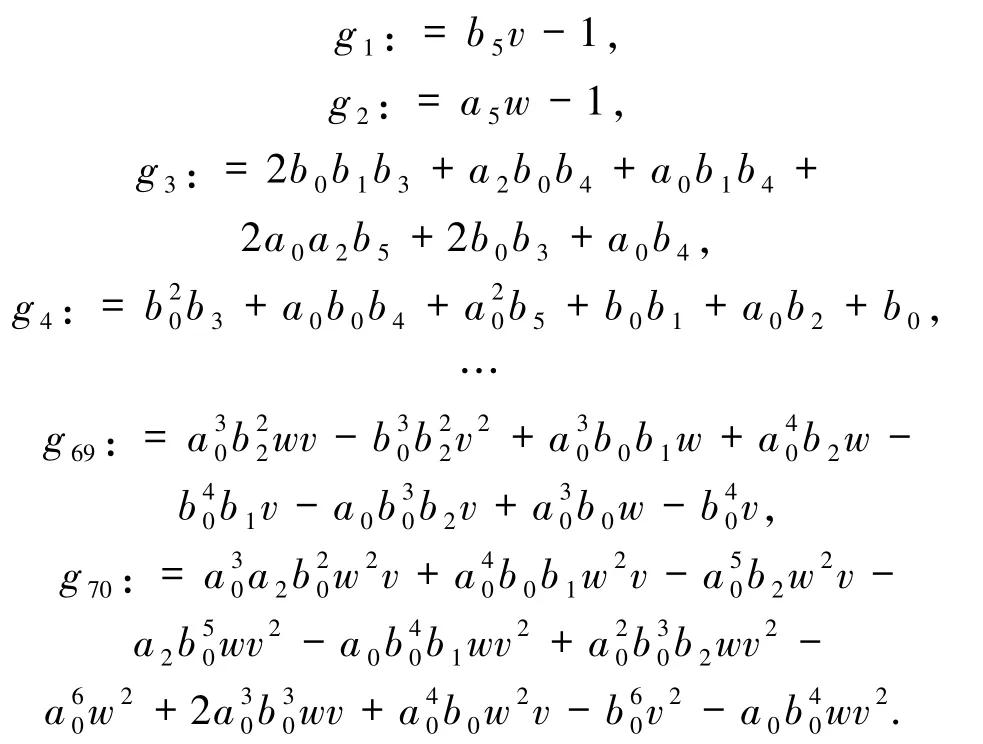
通过简单的计算可知,G ={0}.进一步,运用多项式代数系统Singular 中的命令eliminate 消去变元v、w 并得到一个仅含 ai和 bi的代数系统,记作APSG:={h1=0,…,h29=0},其中
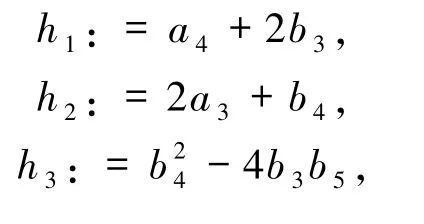
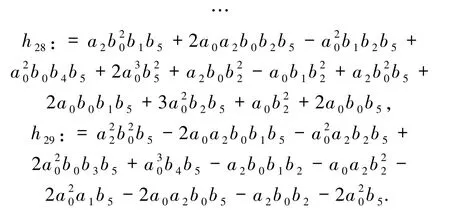
根据算法步骤3,运用Singular 的库primdec. lib 中的命令minAssGTZ 计算APSG 的代数簇的极小不可约分解,并由此获得函数方程(5)的二次平面二次多项式解,即定理中的Ξ5和Ξ6.最后,运用算法步骤4,对上述解进行验根并最终获得条件Ξ5和Ξ6的正确性.定理证毕.
定理3 给出了当迭代次数 n =2 时Babbage 方程(5)平面二次多项式解,实际上,根据文献[29]中定理3.1,当迭代次数n >2 时,上述结论仍成立.
推论 1对任意 n≥2,n∈N,方程(5)存在平面二次多项式解,当且仅当条件Ξ1,Ξ2,…,Ξ6之一成立.
注2实际上,在电脑内存允许的情况下,算法可推广到计算Babbage方程(5)的平面高次多项式解.
4 应用举例
由条件Ξ6可得
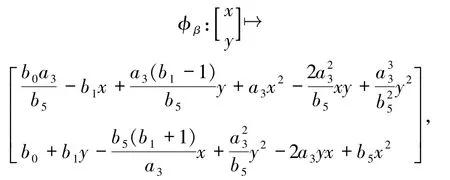
经过简单的计算易得
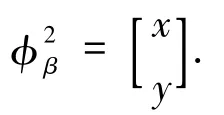
同理可计算出其余几个条件所对应的φβ,且均满足上式.
致谢成都市工匠文化研究中心项目(2020ZC17)对本文给予了资助,谨致谢意.
