一道极坐标方程调考题引发的思考——被忽略的极径

广东 闫 伟

极坐标方程是选修4-4的内容，该试题对于基础较好的学生而言不难，但是根据考试结果看学生得分不高，据多数考生反馈本次考题第一问简单，第二问由于计算量“太大”导致学生无法解出，究其原因笔者认为是学生过分依赖直角坐标方程，理想地认为只要转化到直角坐标方程中就可以解决所有问题，对极坐标方程中极径的本质理解不到位.因此高三复习备考中应强化互化、突出应用、突破用“极”、“直”还是“参”及何时用效果更好.本文从极坐标方程的本质出发来做一些研究.

1.再现学生答题错误

(I)求C1的极坐标方程和C2的直角坐标方程；

下面给出几个典型错误：

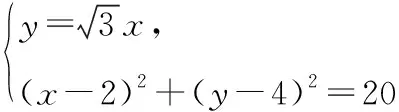
无法继续算下去，这种把希望寄托在直角坐标方程中，殊不知这样算根号中带根号，不能继续化简，后续运算劳而无功，经统计使用这种解法的学生占58.49%.

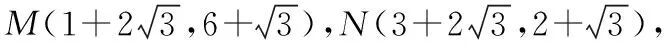
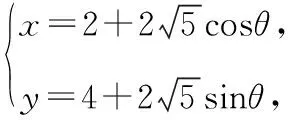
2.错误原因分析

2.1 对教材、考试大纲认识不足

对于极坐标方程，近些年考试大纲明确：(1)了解极坐标方程，了解极角、极径的意义；(2)掌握极坐标方程与直角坐标方程的互化；(3)举例说明解题时用极坐标方程比普通方程更方便，感受极坐标方程的优越感.对于极坐标方程而言：极角的几何意义是极径与极轴所成的夹角，极径是曲线上的点到极点的距离；学习极坐标方程有助于学生进一步体会解题中数学方法的灵活多变，这一点在考查极坐标方程中的极径ρ的几何意义上体现尤为突出.

2.2 思维固化导致解题方法僵化

考试过后，和学生进行深入探讨，分析无法解答的原因，大部分学生反映，由于对直线和圆以及圆锥曲线较熟悉，所以解题时严重依赖直角坐标方程，只想着在直角坐标系中求解，而不想去接受“新知识”、“新方法”，对于该掌握的知识和方法没有掌握好，更谈不上灵活应用，导致一些试题陷进就束手无策了；如本题第(Ⅱ)问是不适合用直角坐标方程求解的，不然计算量很大，也很容易出错.

2.3 知识系统不完善，师生重视不够

部分老师认为极坐标方程这一部分是送分的，新课快速讲完，几乎不怎么复习，就直接开始高三一轮复习；对于学生的学习状况停留在答案对就行的层面，以为学生会用直角坐标方程解答就能应对一切，没有对这部分内容进行深入的分析，没有构建完善的知识体系.对于学生而言可能只会进行“直”“极”“参”之间的转化，只会在直角坐标方程中解答，但是纵观近些年的高考题，极坐标方程的问题一旦转化成直角坐标方程，就掩盖了其几何意义，使得运算量繁杂，甚至无法顺利完成.笔者分析了近期学生的作业，利用极坐标来解答的题型学生都难以应对.

3.利用极坐标方程解答几类常见的题型

笔者整理了近年来在高考和模拟考中经常出现的利用极坐标方程中ρ的几何意义来解答的试题.

类型1.求线段长度的最值

(Ⅰ)求C2与C3交点的直角坐标；

(Ⅱ)若C1与C2相交于点A，C1与C3相交于点B，求|AB|的最大值.

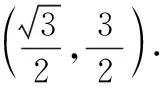
评注：本题考查参数方程、极坐标方程化为普通方程和极径的几何意义，利用极径表示两点间的距离，再利用三角化一求最值；要求学生掌握极径的应用——表示两点间距离.

类型2.求线段比的最值

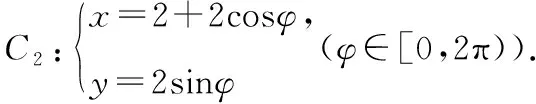
(Ⅰ)写出C1，C2的极坐标方程；

解析：(Ⅰ)易求得C1，C2的极坐标方程分别为ρ(cosθ+sinθ)=1，ρ=4cosθ；

评注：本题考查三种方程间的转化，注意消参与转化公式的灵活应用；另外，应用极坐标中极径的几何意义可求过极点的弦长，解题中要合理运用这些方法.

类型3.求数量积

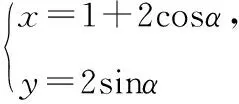
(Ⅰ)求曲线C的极坐标方程；

(Ⅱ)若直线l与曲线C交于A，B两点，求|OA|·|OB|的值.

解析：(Ⅰ)易知C的极坐标方程为ρ2-2ρcosθ-3=0.

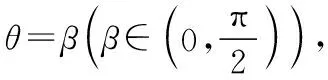
评注：本题考查参数方程化为普通方程与极径的几何意义；将直线化成极坐标方程代入圆的极坐标方程中，根据一元二次方程的根与系数的关系和极径的几何意义求解.

类型4.求面积

评注：本题考查极坐标方程以及参数方程的应用，重点是极径与极角的几何意义的应用，考查综合应用所学知识的能力，解答问题的能力，需要学生积累关于极径解题的经验.

类型5.求参数

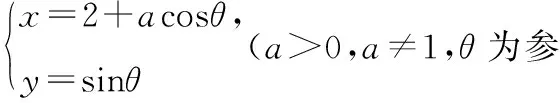
(Ⅰ)若a=2，求曲线M的极坐标方程；

解析：(Ⅰ)易求得曲线M的极坐标方程为ρ=4cosθ.

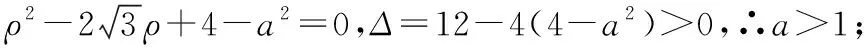
评注：本题考查极坐标与参数方程的知识，关键是明确极坐标系中ρ和θ的意义，从而利用极坐标方程建立关于参数的等式来求解参数和距离.

类型6.求轨迹方程

例6.(2019·全国卷Ⅱ·文22理22)在极坐标系中，O为极点，点M(ρ0，θ0)(ρ0>0)在曲线C:ρ=4sinθ上，直线l过点A(4，0)且与OM垂直，垂足为P.

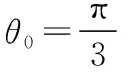
(Ⅱ)当M在C上运动且P在线段OM上时，求P点轨迹的极坐标方程.

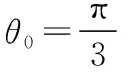
评注：本题主要考查极坐标方程的应用，解题的关键是借助直角三角形边角关系建立ρ和θ的等式，再根据P的位置确定极角的取值范围，要求学生熟练运用极坐标方程进行运算.

极坐标方程的应用不只是在选考题中体现，还可以用它来巧妙地解决圆锥曲线中其他类型的问题，可以大大地降低运算的复杂度，在解题教学中值得推广.

4.利用极坐标方程巧解圆锥曲线问题

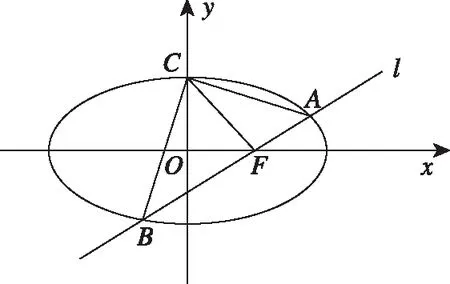
类型1.求椭圆方程

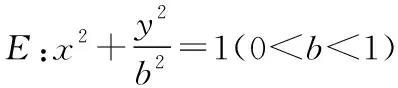
类型2.求离心率

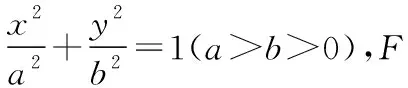
类型3.求线段长最值

例9.设抛物线y2=2x的右焦点为F，过点F的直线交抛物线于A，B两点，则|AF|+4|BF|的最小值是________.

类型4.求面积最值

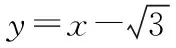
(Ⅰ)求椭圆的标准方程；

(Ⅱ)过F1作两条互相垂直的直线l1，l2，与椭圆分别交于P，Q，M，N四点，求四边形PMQN面积的取值范围.

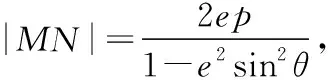
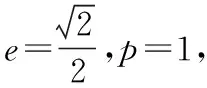
类型5.求参数

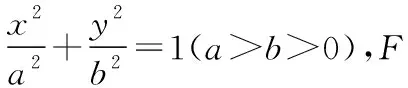
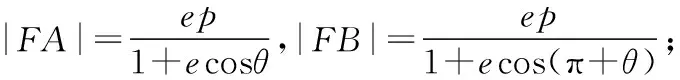
评注：利用极坐标的几何意义解圆锥曲线问题的类型很多，在此不一一列举，运用角度形式的极径解题，不但可以秒杀一类涉及圆锥曲线中过焦点的弦的相关问题，而且避免了联立方程组带来的极其复杂的运算，相比标准答案提供的解法，文中介绍的方法不仅省时省力，且准确率高，但很多学生会忽略这种解题的方法，希望教师在复习备考时应多引导学生关注极坐标方程中极径的几何意义的应用，这样会事半功倍.

5.教学启示

近些年全国卷关于极坐标与参数方程的选考题考查类型比较平稳，一般第一问是三类方程的互化，第二问经常会出现最值问题、长度问题、面积问题、轨迹问题、函数问题、存在性问题等，难度有加大的趋势，考查内容逐渐向几何意义靠拢，化为普通方程解答计算量大，思维的难度也大，切实体现了极坐标与参数方程解题的优越性；所以解决此类问题的思路通常是：若方程的几何意义不明显，可以考虑转化为直角坐标方程，用普通方程的方法解决；若方程的几何意义明显，则用参数方程和极坐标方程解题会更简单.在复习备考中，要让学生强化对极坐标与参数方程本质的理解，重点突破解题中用“极”、“参”还是“直”，灵活应对选考题中各类问题，从而提高复习备考效率.