基于改进Fisher判别准则的卷积神经网络设计

徐小雨,赵龙章,程晓月,何志超

(南京工业大学 电气工程与控制科学学院,南京 211816)

0 概述

卷积神经网络(Convolutional Neural Network,CNN)[1-2]是用于处理二维数据的多层神经网络,其可以自动学习图像特征。根据生物学中的感受野[3]概念,深度学习领域通过引入卷积与激活等结构模仿生物的视觉感知机制,并在20世纪80年代建立视觉感受野模型[4]。之后,纽约大学的LECUN于1998年提出LeNet-5卷积神经网络模型[2],其在手写数字识别中取得了突破性进展。2012年,深度神经网络模型AlexNet[5]以巨大的优势在2012 ImageNet[6]竞赛中获胜,给传统机器学习带来了巨大冲击,同时引发卷积神经网络的研究热潮,使得深度学习技术受到越来越多研究人员的关注。此后,VGGNet[7]、ResNet[8]、ZFNet[9]及GoogleInceptionNet[10]等一系列CNN模型被相继提出,CNN优化方法也不断出现。结构化稀疏学习(Structured Sparsity Learning,SSL)[11]能使模型结构更加紧凑,并且提升了其运行速度。文献[12]利用一系列优化方法将不可微分的t0范数正则项加入目标函数,使得稀疏网络具有更好的泛化能力。文献[13]利用教师网络的高层神经元输出来表示需要迁移的领域知识,使学生网络可以获得更高的压缩率。文献[14]基于LASSO正则化剔除冗余卷积核与其对应的特征图,然后重构剩余网络。文献[15]提出使用最小平方误差函数的代价函数,使其在样本数量较少的情况下依然能够保持较高的分类准确率或使模型更快的收敛。在文献[16-17]工作的基础上,文献[18]提出基于改进Gabor滤波器的卷积神经网络模型,引入曲度系数概念对传统Gabor滤波器进行改进,使得改进的Gabor滤波器在具备方向和尺度特性的同时兼具良好的局部曲率响应特性。

本文借鉴Fisherface[19]方法的思想,设计一种基于改进Fisher判别准则的CNN(FDCNN)网络结构,使用CNN学习从输入图像到多维欧式空间的映射关系,并将改进的Fisher判别准则作为网络模型的损失函数,以提高FDCNN在实际应用中的灵活性。

1 基于改进Fisher判别准则的CNN设计

1.1 基于距离度量的分类方法

本文提出一种基于距离度量的分类方法,其利用CNN将图像映射为一个相似向量,通过比较相似向量之间的距离判别图像类别。由于卷积部分依据具体任务学习从图像到向量的映射关系,因此在模型训练完成后只要分类任务没有变化,该映射关系就一直有效,即使数据集发生变化也无需重新训练模型。准确而言,该方法属于验证问题,即比较两个输入是否为同一类,其能同时应用于验证任务及图像识别与检索任务。图1为基于距离度量的分类过程,其中黑色点为该类样本相似向量的均值,在识别任务中通过比较待识别数据与各类样本相似向量的平均值之间的距离确定待识别样本的类别。

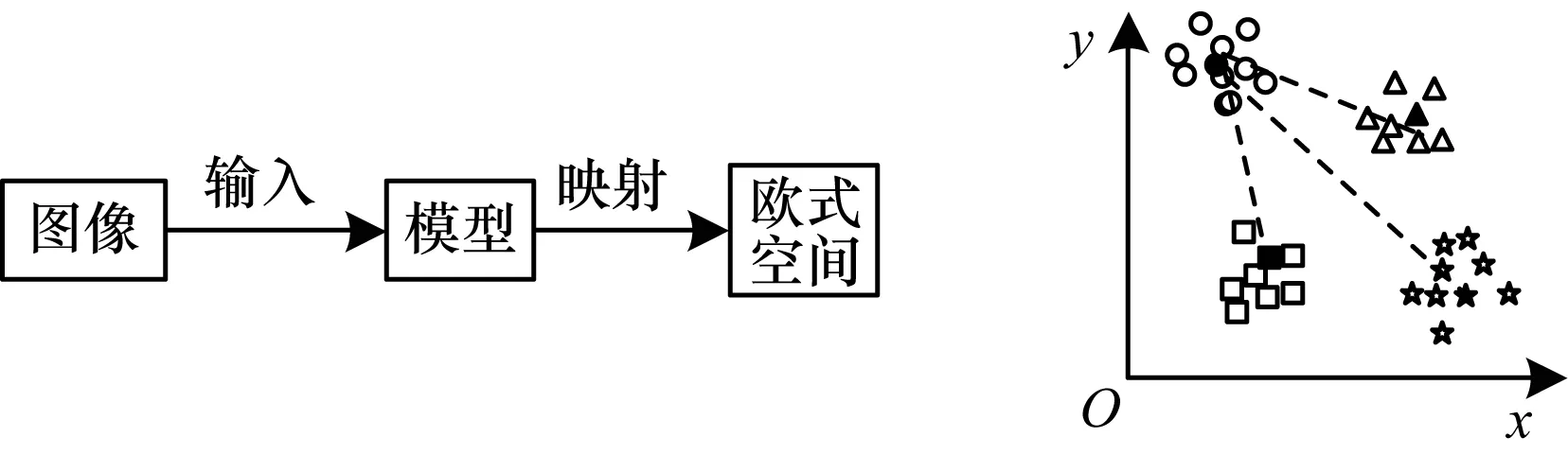
图1 基于距离度量的分类过程

1.2 损失函数及其反向传播方法

Fisher判别准则基于传统线性判别法,其主要思想是为达到最佳分类目的,需求解最优投影方向,将样本数据投影到低维空间中,在保证相同类别样本投影向量之间距离尽量小的同时,不同类别样本投影向量之间的距离尽量大。基于Fisher判别准则的损失函数表示为:

(1)

其中,判别函数J为关于投影方向w的函数,JB为类间离散度,JW为类内离散度,SB为类间离散度矩阵,SW为类内散度矩阵。

本文将CNN看作是从图像到相似矩阵的一种非线性映射关系,对于图像样本集X={x1,x2,…,xN},模型输出为:

V(xi)=Net(xi)

(2)

其中,Net(·)为非线性映射,即CNN前向计算过程,V(xi)为模型对样本集X中第i个样本xi经过非线性映射输出的相似向量。

类内离散度表示为:

(3)

类间离散度表示为:

(4)

当式(1)取最大值可以保证类内离散度尽量小的同时,类间离散度尽量大,因此理论上其可以作为训练模型的损失函数,但在神经网络反向传播时需要将其对各权重参数进行梯度求解,而式(1)为分式形式且分子分母都有权重参数,由于对各权重求梯度时太过复杂,且要在保证类内离散度尽量小的同时,类间离散度尽量大,因此基于改进Fisher判别准则的损失函数为:

J=JW-γJB

(5)

其中,JW和JB分别表示各输入数据在非线性映射空间中的类内离散度和类间离散度,γ为两种离散度的权重系数。式(5)不仅能保证类内离散度尽量小的同时,类间离散度尽量大,而且与式(1)相比,其大幅降低了权重求梯度的计算量。

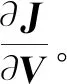
(6)

其中,V(xi)d为输出层的第d个节点。

同理可以得到类间离散度JB的输出层节点的残差计算推导过程为:

(7)

根据式(6)与式(7)可得,对于损失函数J,其输出层节点的残差计算公式为:

(8)

在模型训练时,对损失函数使用式(8)求得输出层的残差后,就可通过反向误差传播方法对网络权值进行更新。式(5)中的γ为类内与类间离散度的权重系数,权重系数的选取会对模型准确性产生较大影响,而γ值的选取则会影响模型的分类效果。

1.3 损失函数有效性验证

本文在MNIST数据集上进行实验验证,特征提取阶段的网络结构如图2所示,包括卷积计算层(Conv)、最大池化层(Max Pool)、全连接层(FC),其中Conv 5×5s1,256/ReLU表示使用5×5大小的卷积核,步长设置为1,通道数为256,对卷积后的值使用ReLU激活函数,ReLU激活函数的运用减少了参数的相互依存关系,缓解了过拟合问题。将图2中的网络结构分别应用于本文基于改进Fisher判别准则的CNN与传统CNN进行对比实验,其中:本文基于改进Fisher判别准则的CNN将图2的输出作为多维欧式空间中的相似向量,然后使用基于Fisher判别准则的损失函数(见式(5))对网络模型进行训练直至收敛,其中γ取1.1;传统CNN将图2的输出作为softmax的输入,使用交叉熵作为该softmax分类器的损失函数。

图2 特征提取阶段的网络结构

图3和图4为测试样本分别经过两个CNN特征提取阶段后,使用t-SNE算法降到二维后的可视化结果。

图3 传统CNN特征提取后的可视化结果

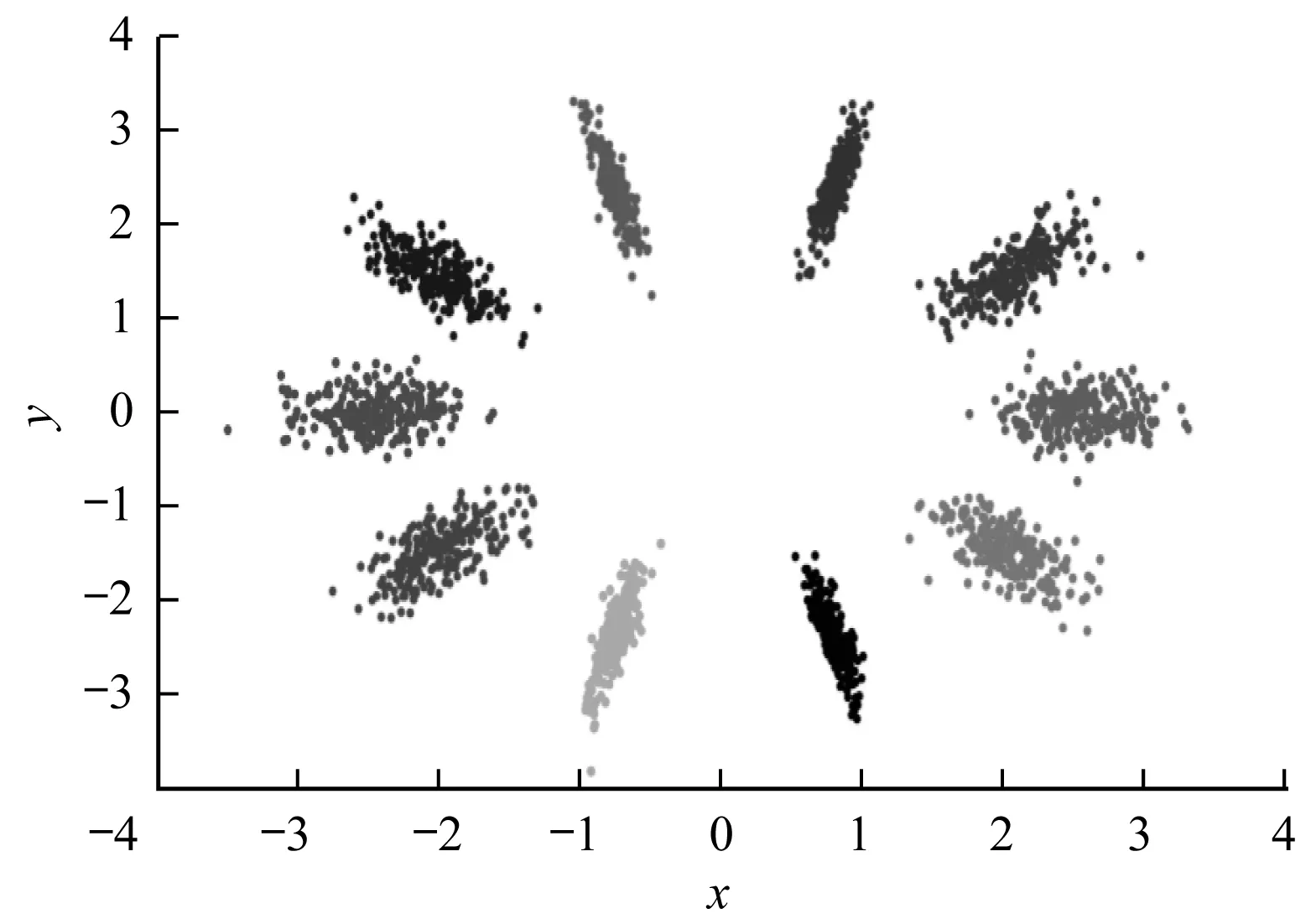
图4 本文CNN特征提取后的可视化结果

图3中样本的类内离散度较小,同类之间的数据有重叠与交叉部分,而图4中每一类类内样本离散度较小,而类间离散度较大,更有利于分类,从而证明本文基于改进Fisher判别准则的损失函数能增大类间距离的同时减小类内距离,提高分类性能。

1.4 网络结构设计

本文设计一种GRV网络模块,其借鉴GoogleNet的Inception思想,使用3个不同尺寸的卷积增加网络对不同尺度特征的适应性,并且使用1×1的卷积结构减少参数个数的同时跨通道融合信息,降低模型复杂度,并提高网络表达能力。同时,GRV结合了ResNet的残差学习模块,可在一定程度上减少信息丢失,并且借鉴VGGNet中多个小卷积层替代单个大卷积层的思想提高了模型精确度。GRV网络模块如图5所示。

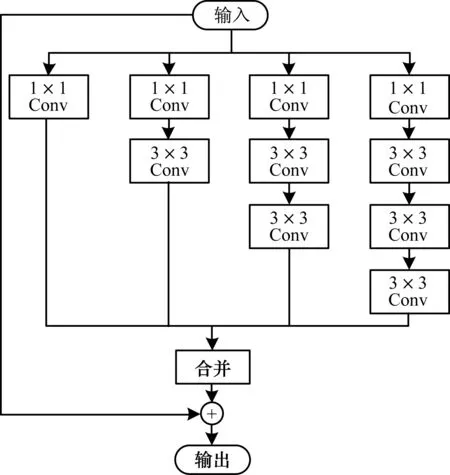
图5 GRV网络模块

本文将GRV模块引入到CNN网络中,设计FDCNN人脸识别网络,并使用基于改进Fisher判别准则的损失函数对网络模型进行训练,如图6所示。

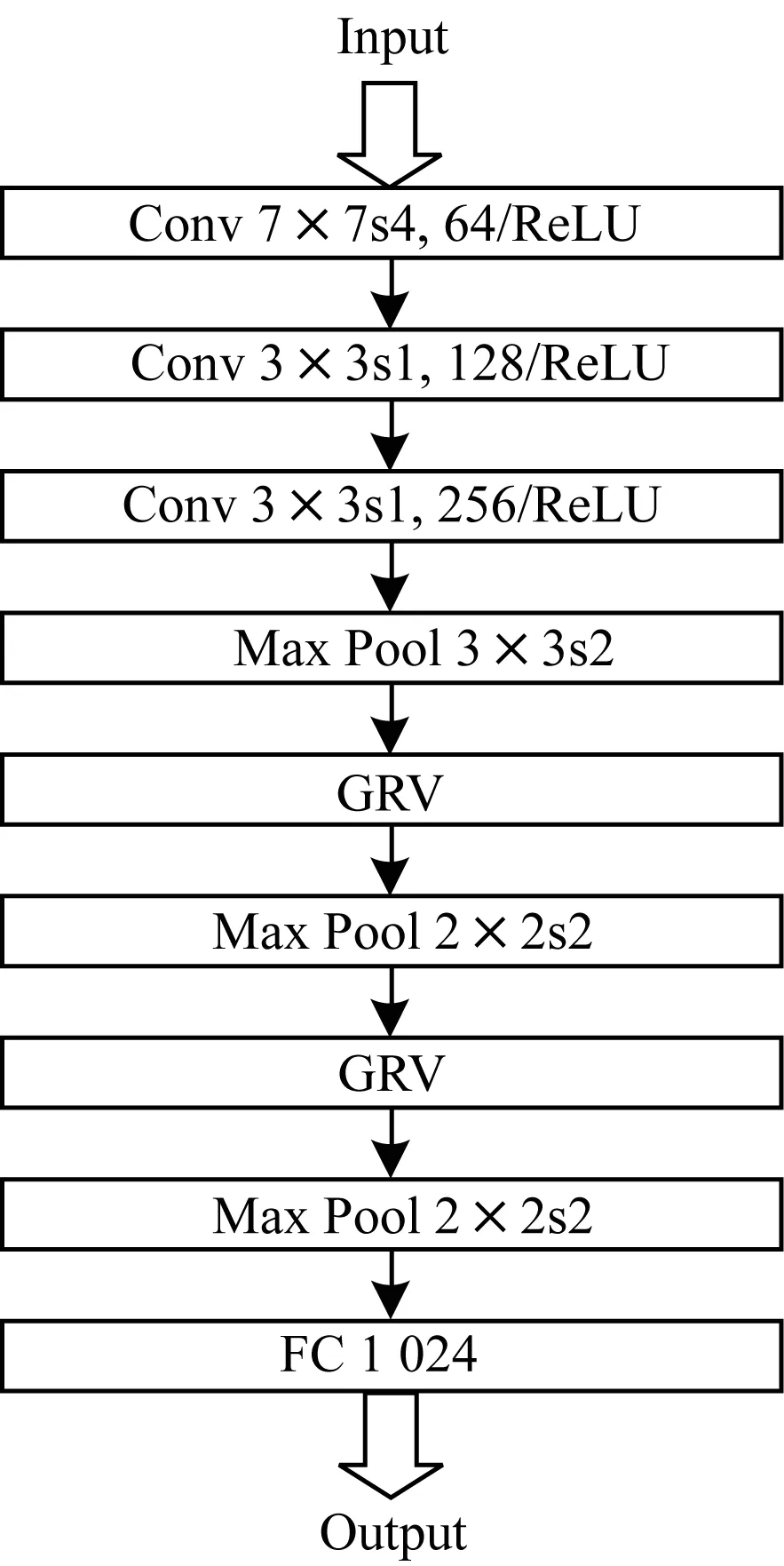
图6 FDCNN人脸识别网络结构

2 实验结果与分析

2.1 数据集选择与设置

本文使用CBCL人脸数据集对网络模型进行训练与测试,并采用ORL人脸数据集对其进行测试。图7为ORL数据集部分图像。由于CBCL数据集与ORL数据集图像较清晰,且图像中的人脸都占主要部分,因此图像预处理只需将图片分辨率调整为128像素×128像素。

图7 ORL数据集部分图像

2.2 损失函数的参数确定

为给式(5)中损失函数的参数γ选取一个合适的值以实现较好的分类效果,本文在MNIST数据集上进行验证,将FDCNN作为网络模型,分别对取不同γ值的损失函数进行训练并测试最终的识别率。不同γ值时的识别率如表1所示。可以看出,γ取不同值会对识别率有一定影响。当γ取值为0.5～1.1时,模型识别率不断增加;当γ取值为1.3和1.5时,模型识别率不断降低;当γ取值为1.1时,模型识别率最高,因此γ=1.1为最佳取值。

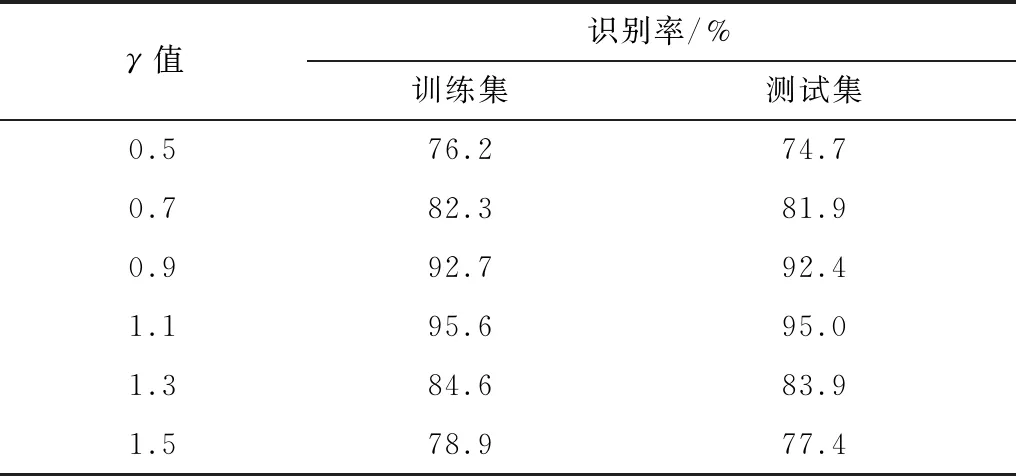
表1 不同γ值时的识别率对比

为进一步验证γ为1.1时模型的分类效果,分别使用不同γ值求得测试样本的相似向量,并使用t-SNE算法将该相似向量降到二维,得到不同γ值时测试样本相似向量的可视化结果如图8所示。

图8 不同γ值时测试集的可视化结果

可以得出,当γ值较小时,不同类之间的距离所占比重小,类内距离对分类的影响较大,此时随着γ值的增加,不同类之间的距离会缓慢增大,但是继续增加γ值会使类内离散度所占比重越来越小,直至不同类间的距离对分类的影响占主导作用,此时虽然类间的距离很大,但是类内离散度也很大,导致分类效果不理想,且随着γ值的不断增加,类内离散度随之增大,分类效果也急剧变差。由此可见,γ值并非越大越好,从表1和图8可以看出,当γ取值为1.1时,模型分类效果最佳,因此式(5)中基于改进Fisher判别准则的损失函数的γ取值为1.1。

2.3 对比实验

将FDCNN网络模型与传统CNN网络模型和文献[18,20]网络模型进行多组实验,并将结果进行对比与分析,验证FDCNN网络模型的有效性,其中:文献[18]网络模型在传统CNN损失函数的基础上,将Fisher判别准则中的类内离散度与类间离散度以一定的权重添加到交叉熵损失函数中,并使用该损失函数对具有不同数量训练样本的网络模型进行训练,并测试模型最终识别率;文献[20]网络模型使用基于改进Fisher判别准则的损失函数对全连接神经网络进行训练。将CBCL数据集如表2所示进行训练集和测试集设置,并对4种网络模型进行训练与测试,在训练样本数量不同时的识别率如表3所示。

表2 CBCL训练集与测试集设置

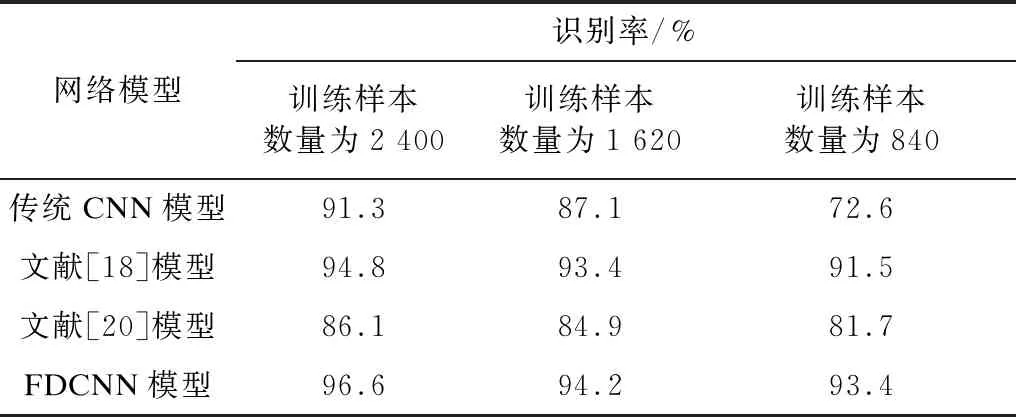
表3 CBCL数据集上的识别率对比

从表3可以看出,随着训练样本数量的减少,识别率不断降低,而本文FDCNN网络模型无论是在训练样本数量为2 400时还是训练样本数量为840时,识别率都为最高,当训练样本数量为840时,识别率为93.4%。文献[20]网络模型属于全连接神经网络,在训练样本数量为2 400时,其识别率低于传统CNN网络模型,但是由于其损失函数基于改进的Fisher判别准则,因此在训练样本数量为840时,其识别率反而高于传统的CNN网络模型。文献[18]网络模型也使用了基于改进Fisher判别准则的损失函数,但由于本文FDCNN使用GRV模块,因此其最终识别率高于文献[18]网络模型。

通过在CBCL人脸数据集上使用不同训练样本得到的本文FDCNN网络模型对ORL人脸数据集中的人脸进行识别,以验证该网络模型在不同数据集上的泛化能力。训练得到的FDCNN网络模型在ORL人脸数据集上的识别率如表4所示。

表4 ORL数据集上的识别率对比

由于本文设计的FDCNN网络模型不是学习从图像到类别的拟合过程,而是学习从图像到多维欧式空间的映射关系,其是一种基于距离度量的机器学习方法,通过比较两输入图像得到的相似向量之间的欧氏距离来判别其是否属于同一类别。一旦模型训练完成,在识别过程中即使数据集发生变化,但是由于该映射关系已经建立,因此仍可以通过比较向量之间的距离进行分类识别。从表4可以看出,虽然在ORL数据集上的识别率略低于在CBCL数据集上的识别率,但是其降低的幅度很小,即训练得到的FDCNN网络模型的泛化能力较强。

3 结束语

本文提出基于改进Fisher判别准则的卷积神经网络(FDCNN)。利用基于距离度量的分类方法,设计基于改进Fisher判别准则的损失函数训练模型,并综合VGGNet、GoogleNet和ResNet网络结构的特点,通过引入GRV模块的CNN网络进行人脸识别。实验结果表明,FDCNN网络模型具有较好的人脸识别性能及泛化能力。后续将从CNN运算速度、训练时间及训练过程中容易陷入局部极小值等方面进行深入分析与优化研究,进一步扩大FDCNN网络模型的适用范围。