基于泊松簇过程的毫米波异构网络频谱分析

陈玉宛,贾向东,2,纪澎善,吕亚平

(1.西北师范大学 计算机科学与工程学院,兰州 730070; 2.南京邮电大学 江苏省无线通信重点实验室,南京 210003)

0 概述

无线数据业务流量的指数级增长和频谱资源的短缺,推动了新的无线通信网络技术的发展。为满足日益增长的网络吞吐量的需求,必须考虑新技术来设计下一代5G蜂窝网络。工业界和学术界普遍认为,异构网络(Heterogeneous Networks,HetNets)和毫米波(mm-Wave)是未来5G蜂窝网络容量增长的两项关键技术[1]。

高通公司定义HetNets[2],其由宏小区和具有低发射功率的小小区共同组成。低功耗小型基站的部署,可以提高系统网络容量,增强覆盖范围并消除覆盖盲点[3]。此外,由于HetNets的不规则性和异构性日益增加,为了提供一个系统级的分析框架,随机空间模型、统计几何和点过程理论工具被用于精确建模和简化分析[4-5]。目前最流行的方法是将HetNets建模为多层独立泊松点过程(Poisson Point Process,PPP)的叠加网络[6],其中每层由不同类型的基站(Base Station,BS)构成。该方案的网络节点在空间上呈均匀分布,因此没有充分利用5G网络的异构特性。网络元素异构部署的直接后果是在BS和用户设备(User Equipment,UE)的位置上出现了不同类型的空间耦合[7],所以PPP建模不能为上述条件下的干扰提供准确的模型。因此,根据热点形成与UE-BS耦合的潜在联系,文献[8]利用泊松簇过程(Poisson Cluster Process,PCP)对UE分布进行建模和分析[9]。

在大规模热点区域中,随着热点的增加,BS的数量也随之增加。特别是每个簇中UE的级联很大程度上依赖于其所在位置。在不同的位置,目标UE可能与不同的BS相级联,UE性能取决于其位置[10]。基于这些考虑,文献[11]结合部分频率复用(Fractional Frequency Reuse,FFR)和UE分类进行研究分析,然而该方案仅对基于网格的蜂窝网络有效。为克服该问题,文献[12]将该方法推广到基于随机的两层异构网络,并根据信干扰加噪声比(Signal-to-Interference-Noise Ratio,SINR)阈值对蜂窝网络中的UE进行分类。考虑到基于SINR的分类方法会导致目标用户频繁地在中心用户和边缘用户之间切换,文献[13]提出了基于距离比的分析方案。

本文提出一种基于PCP的建模方案,该方案将用户热点的地理中心建模为独立的PPP,其周围的UE、微微基站(Pico Base Station,PBS)和毫微微基站(Femto Base Station,FBS)是分散的,从而形成独立的、非齐次的PCP。利用目标UE与PBS之间的第一和第二最近距离之比对UE簇进行分类,结合随机几何的方法,推导目标UE的级联概率和下行链路(Downlink,DL)的频谱效率,并分析发射功率、UE簇分类因子、PBS分布最大值对级联概率的影响。

1 系统模型与信道假设

1.1 系统模型

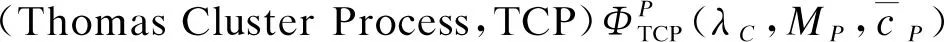
本文为实现系统建模所采用的两种簇过程的定义如下:

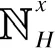
(1)

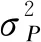
(2)

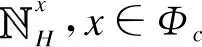
1.2 传输模型

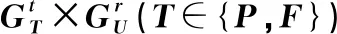
表1 天线增益的值及概率

由于定向波束形成增益较大,本文仅考虑所有无线信号在忽略小尺度衰落的情况下受到较大的路径损耗效应[15]。由于毫米波的一个显著特点是容易受到障碍物的干扰,对于大规模的路径损耗,本文引入视距(Line of Sight,LoS)球来模拟阻塞[16]。在该阻塞模型中,定义视距球半径为μ,即UE与其附近阻塞之间的平均距离。特别地,有且只有当发射器的通信链路距离r小于视距球半径μ时,接收器才会认为该发射器是视距,否则,该发射器是非视距(Non Line of Sight,NLoS)。根据上述模型,得出通信距离为r的路径损耗定律为:

L(r)=U(μ-r)CLr-αL+U(r-μ)CNr-αN

(3)

其中,Ck是截距,αk是路径损耗指数,k=L和N分别表示视距和非视距链路,U(.)是单位阶跃函数。

1.3 簇分类方法

在PBS和FBS簇中,UE会遇到更严重的簇内干扰,从而使性能大大降低。为克服这一问题,本文提出了一种有效的干扰管理方案,即根据UE到PBS(而不是FBS)的第一和第二最近距离比对UE簇进行分类。

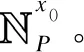
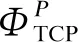
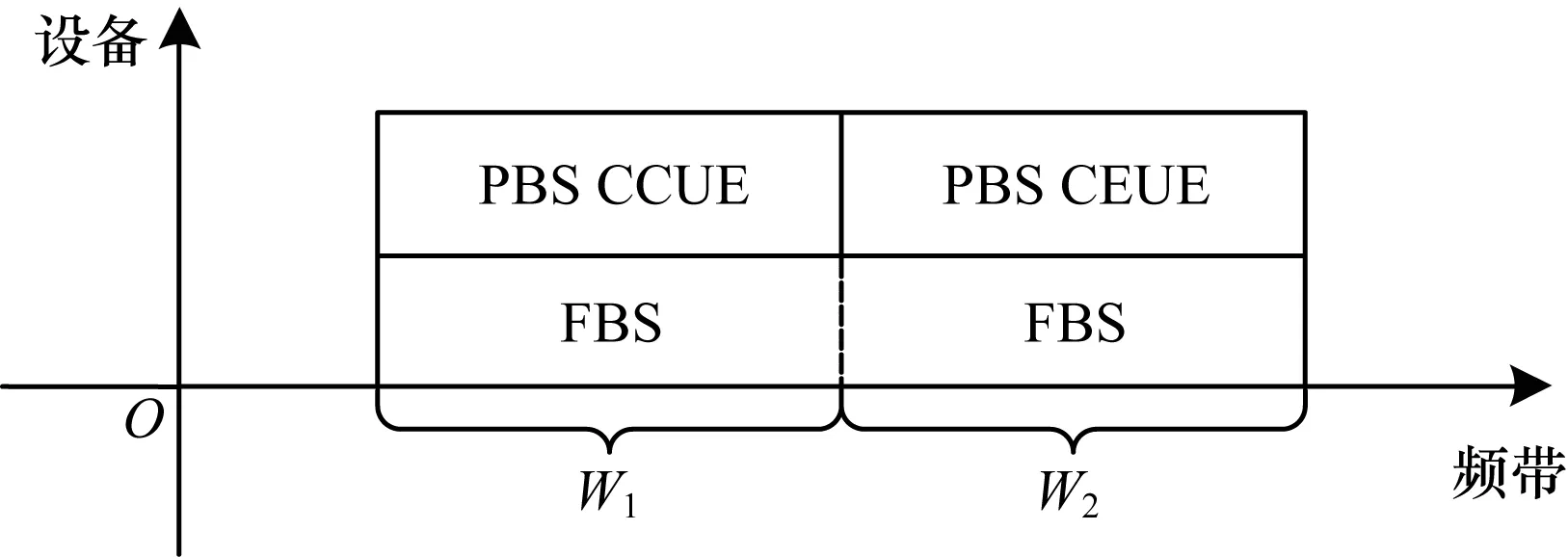
图1 改进的FFR、CCUE与CEUE频谱分配示意图

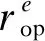
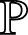
(4)

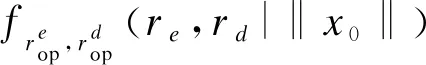
(5)

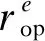
(6)

然后,将式(6)代入式(4),得出把目标UE分类为CEUE的概率:

(7)

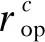
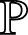
(8)

2 UE级联准则与概率

假设开放访问方案允许用户连接到任何层BS[20-21]。受毫米波信号传播特性的启发,本文提出加权最近距离级联准则。设rop和rof分别为目标UE与PBS和FBS的最近距离。因此,目标UE与PBS级联的概率计算为:

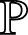
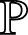
(9)

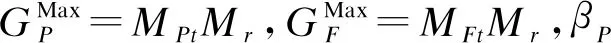
(10)

根据式(9),目标UE与FBS级联的概率为AF=1-AP。式(9)表明,为了实现级联概率AP,需要对最近距离rop和rof进行统计描述。

2.1 CEUE级联概率

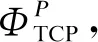
(11)

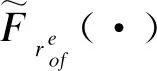
(12)

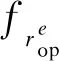
(13)

其中,CE表示目标UE位于簇边缘区域的概率。然后,把式(12)和式(13)代入式(11),得到定理1。

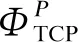
(14)

2.2 CCUE级联概率

(15)

其中,概率CC=(MPξ2)/(MP-1+ξ2)由式(8)给出。然后使用类似于式(11)的定义,得到定理2。

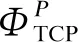
(16)

3 DL频谱效率分析

本节首先给出了目标UE接收到的SINR。结合干扰的拉普拉斯变换和上述的级联概率,推导出相应的DL频谱效率。基于上述描述,给出目标UE的SINR为:

(17)

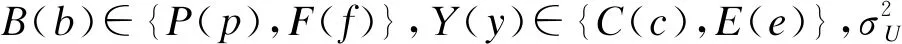
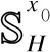
(18)

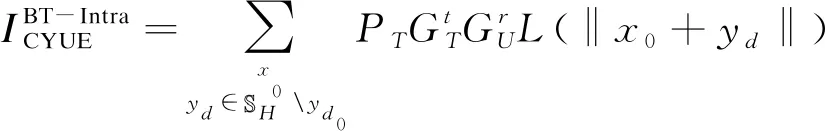
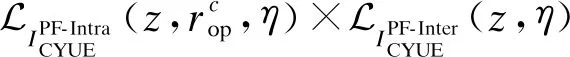
(19)

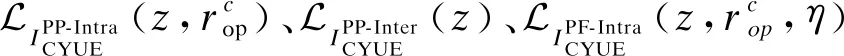
(20)

(21)

(22)

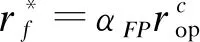
(23)

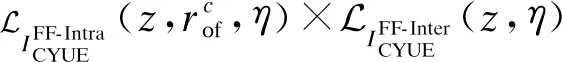
(24)

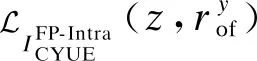
(25)

(26)

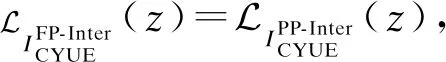
(27)

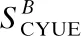
(28)

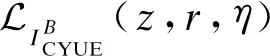
4 仿真结果与分析

通过上述推导和分析,给出仿真和数值结果,验证了推导的正确性,并分析了不同网络参数对可实现的级联概率和频谱效率的影响。本文所有的仿真分析均使用表2所示的参数值。

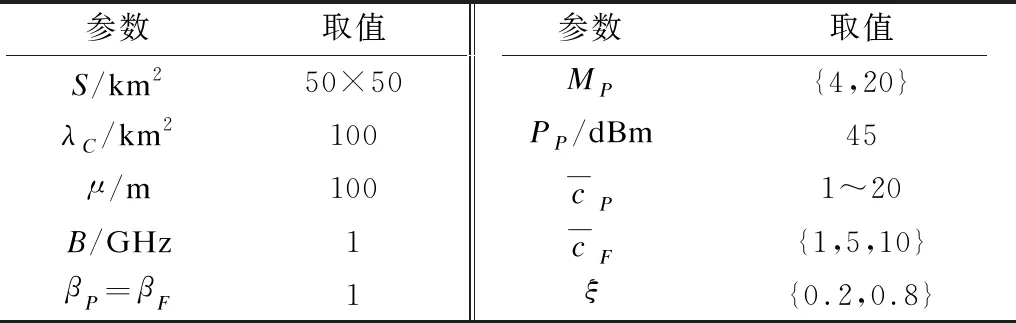
表2 仿真系统参数值

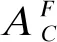
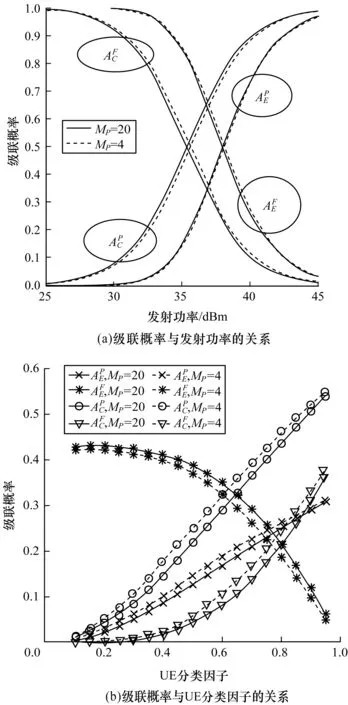
图2 不同网络参数对级联概率的影响

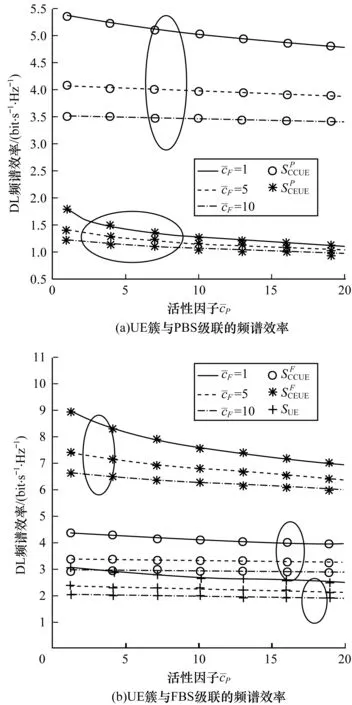
图3 频谱效率与活性因子的关系

5 结束语

本文基于PCP网络模型研究大规模热点区域毫米波异构网络模型的级联概率和频谱效率。在该网络模型下,借助毫米波路径损耗模型和随机几何方法,推导出UE级联概率和频谱效率表达式,并分析了相关参数对系统性能的影响。仿真结果表明,与传统基于PPP的网络模型相比,设置合适的UE簇分类因子可显著提高网络的级联概率和频谱效率。下一步将基于PCP网络模型研究毫米波异构网络的覆盖概率和能量效率。