基于截面曲线方程的螺旋转子建模及数控加工

姜 海， 陈超超， 田春艳

(1.合肥学院 先进制造工程学院，合肥 230601；2.华德控股有限公司 华科技术部，浙江 慈溪 315300)

0 引 言

双转子流量计是一种先进的容积式流量计，具有计量准确、无脉动、噪音低、粘度适应性强等优点，在我国已逐步得到市场认可。[1-3]该流量计中关键功能部件是一对相互啮合的螺旋转子，其结构参数直接影响了流量计的工作性能。[4-5]由于技术垄断等原因，螺旋转子在国外一般都采用成型刀具加工。成型刀具设计制造困难，价格昂贵，且难以满足单件小批量生产要求。因此，结合国内现有实际生产条件，探索采用标准球头铣刀对该类零件进行数控铣削加工，具有一定的理论意义和较高的实用价值。为此，我们和有关企业合作，对螺旋转子的精确建模和多轴数控加工技术开展了研究。

1 螺旋转子的工作原理及轮廓线形分析

双转子流量计的工作原理如图1所示，两个齿形参数、结构尺寸相同，旋向相反的螺旋转子相互啮合，在流体压力作用下，按箭头所示方向平稳均匀地旋转，无主被动之分；同时流体从齿槽与壳体之间的空间一份一份地流到右边的管道，其流量与转子转数成正比。[3]欲使两转子平稳无干涉地转动，必须符合齿廓啮合基本定律，即两转子工作齿面应是一对共扼曲面。同时，为满足容积式流量计两转子之间的密封性要求，两转子轮齿应作无侧隙、无根隙啮合。

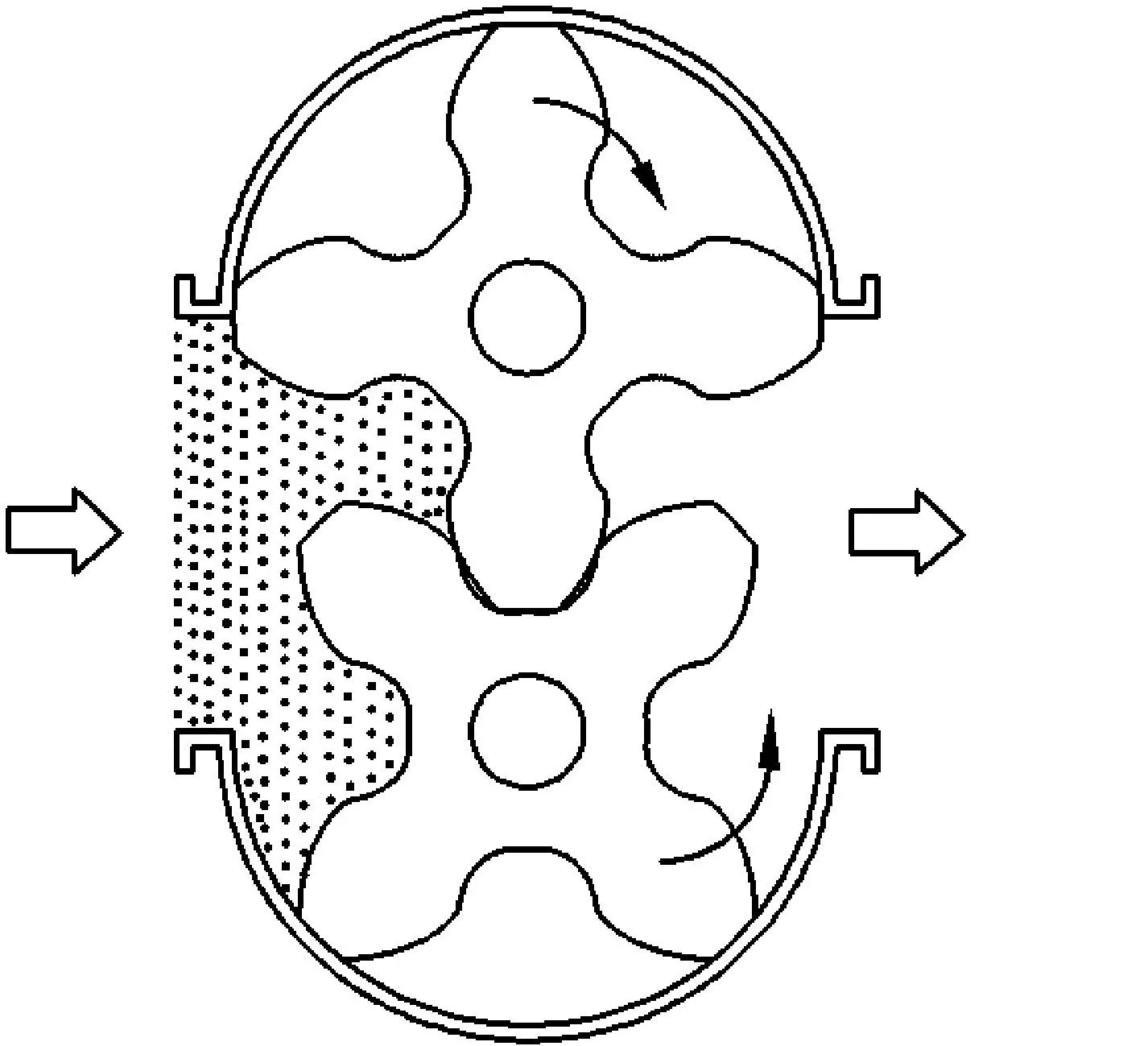
图1 双转子流量工作原理

从啮合原理看，能满足上述要求的齿形有很多。考虑到制造方便、流量计容积空间最大等因素，经分析研究设计了由渐开线和过渡曲线组成的复合齿形，其截面形状由齿顶圆弧、渐开线、过渡曲线、齿根圆弧等组合而成，如图2所示。这样螺旋转子可以描述为大模数、小齿数的斜齿轮。与一般的斜齿轮不同，为满足两转子啮合转动时密封性的要求，转子在工作时其双面齿廓、齿顶圆和齿根圆都必须参与啮合；[6]同时由于齿数小(例如只有4齿)，啮合传动时轮齿会发生根切现象，[7]故形成了截面轮廓中的过渡曲线。因双转子流量计的两转子属平面啮合，转子的螺旋型曲面是其端面齿形作螺旋运动形成的，故转子设计制造须解决的核心问题是精确求取其截面轮廓曲线。

2 螺旋转子的数字化精确建模

根据上述对螺旋转子轮廓线形的分析，可以对各曲线段建立函数方程表达式，以求取螺旋转子截面轮廓曲线，从而对转子进行数字化建模。考虑到后续应用UG软件建模的方便，宜采用直角坐标参数方程形式。

2.1 截面轮廓渐开线方程的建立

螺旋转子截面轮廓中，与齿顶圆弧相邻的部分为渐开线。如图3所示，渐开线是一直线(即发生线CP)沿一半径为rb的圆周(即基圆O)作纯滚动时，直线上任一点P所形成的轨迹EPS。[7]图中，θ是渐开线的展角，t是发生线与y轴的夹角。

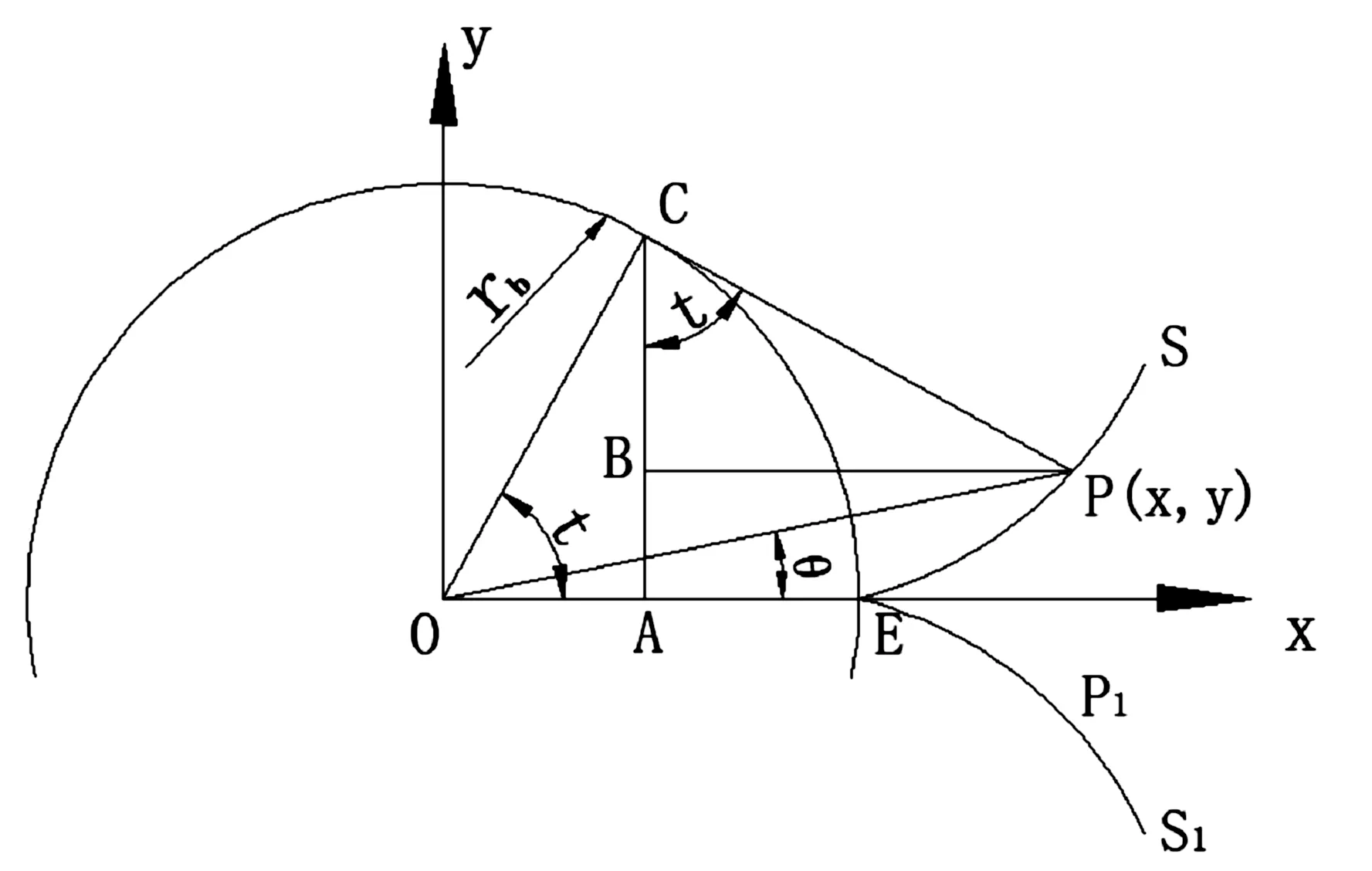
图3 截面轮廓渐开线方程的建立

当渐开线从基圆与X轴交点E作为起始位置时，t和θ取值均从0开始增大。由图，渐开线EPS上任一点P的X坐标为：

x=OA+BP=rbcost+CPsint

(1)

因发生线CP沿基圆O作纯滚动，故CP与圆弧段CE相等，即CP=rb×t

代入(1)式则有：

x=rbcost+rbtsint

(2)

同理，渐开线上任一点P的Y坐标为:

y=rbsint-rbtcost

(3)

由(2)、(3)即得渐开线EPS的直角坐标参数方程为：

(4)

相应地，与y轴对称的另一方向渐开线EP1S1的直角坐标参数方程为：

(5)

上述曲线函数方程的参变量为t，t∈[t1,t2]。

2.2 截面轮廓过渡曲线方程的建立

螺旋转子截面轮廓中，与齿根圆相邻的部分为过渡曲线，它是因小齿数斜齿轮啮合传动时轮齿发生根切而形成的，也是研究的重点和难点。如前图2所示，根据范成运动加工共轭齿廓的原理，当两转子啮合传动时，转子上两直径相等的节圆相切并作无滑动的滚动；它可视为一转子固定不动，而另一转子的节圆沿固定转子的节圆作纯滚动。[7]因转子齿顶圆和齿根圆都参与啮合，故在此过程中，滚动转子轮齿的齿顶边缘点B生成的轨迹即为两转子啮合时因根切所形成的过渡曲线。

现以固定转子截面中心O为原点建立坐标系，如图4所示。设在初始位置时，两转子节圆的相切点在滚动转子上为点P，滚动转子中心A和齿顶边缘点B的连线AB与两转子中心连线AO的夹角为δ(即齿顶圆齿厚对应圆周角的一半)；当滚动转子节圆沿固定转子节圆作纯滚动转过t角度时，原滚动转子中心点A到达C点，原相切点P到达点K，原齿顶边缘点B到达点D，而两转子节圆的相切点则变为点N。

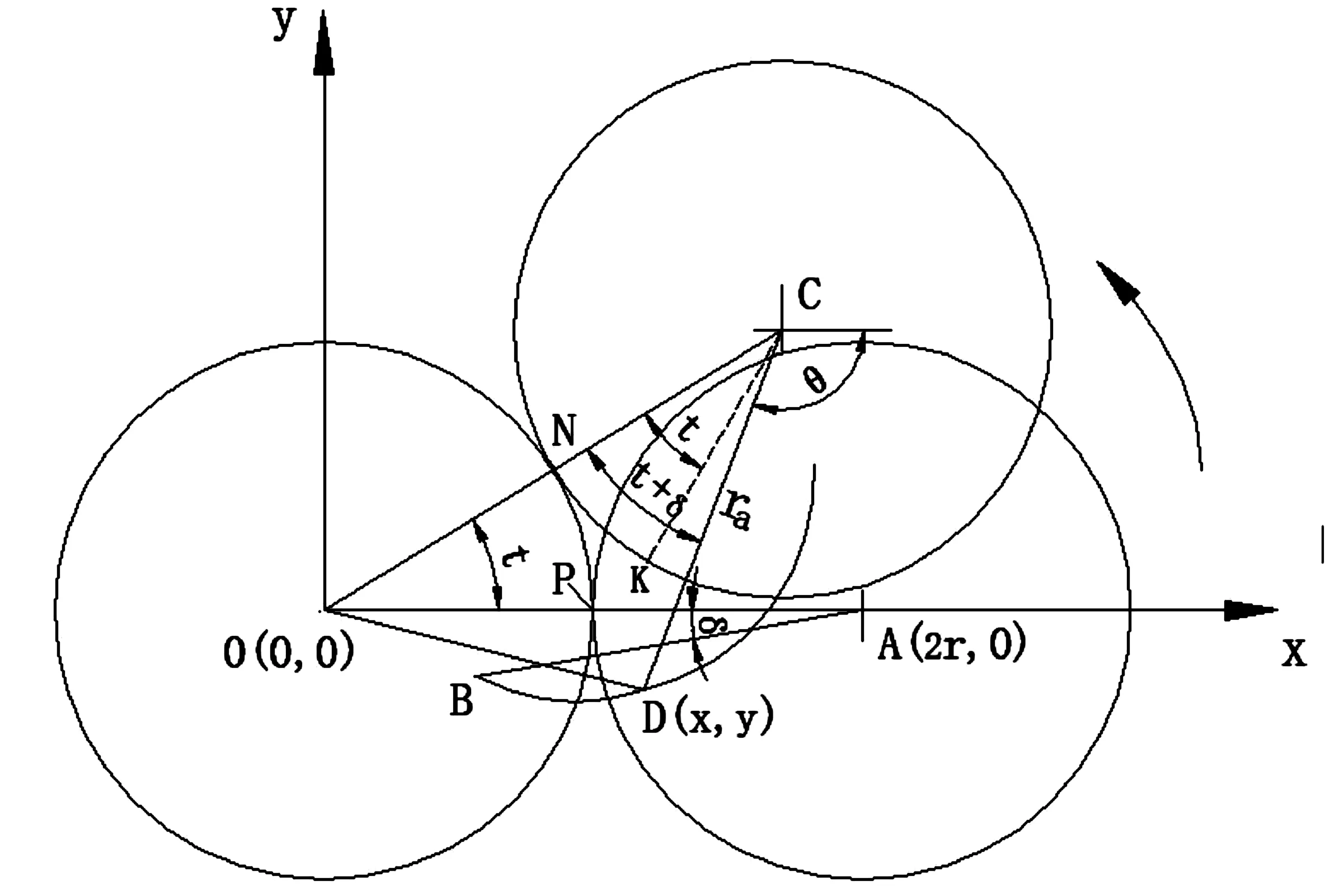
图4 截面轮廓过渡曲线方程的建立

因两转子截面形状相同，故可设两转子的基圆半径均为rb，两转子的齿顶圆半径均为ra，两转子的节圆半径即为分度圆均半径r，此时AB= CD =ra；因滚动转子作纯滚动，由图4知圆弧NK长度等于圆弧NP长度，

故有

∠NCK=∠NOP=t

此时，有：

θ=-(π-t-t-δ)=-(π-(2t+δ))

(6)

设滚动转子齿顶边缘点D的坐标为(x,y)，由图有以下几何向量关系：

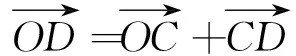
(7)

其中

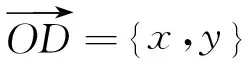
(8)

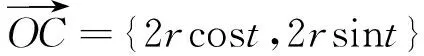
(9)

(10)

将(6)式代入(10)式即有：

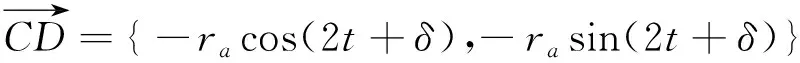
(11)

将(8)、(9)、(11)式代入(7)式，即得：

{x,y}={2rcost-racos(2t+δ),2rsint-rasin(2t+δ)}

(12)

故

(13)

公式(13)即为螺旋转子截面轮廓过渡曲线的直角坐标参数方程；该函数方程的参变量为t，t∈[t1,t2] 。

此外，滚动转子的齿顶圆弧段在两转子节圆作纯滚动过程中，包络形成了另一转子的齿根圆弧段，它与上述过渡曲线段相切。至此，转子截面轮廓各曲线段形式均已确定。

2.3 螺旋转子建模实例

现给定一对相互啮合的螺旋转子，已知的基本参数如下：

两转子中心距81mm，转子齿数4，端面模数20.25mm，法向压力角20°，导程405mm。

按上述基本参数，易求得螺旋转子建模设计所需的其它参数，如分度圆半径r、基圆半径rb、齿顶圆半径ra、齿根圆半径rf、齿顶圆齿厚Sa、齿顶圆齿厚对应的半圆周角δ等。然后在UG软件中，按以下基本步骤进行建模。[8]

(1)通过UG的“表达式”功能，根据式(5)、式(13)，输入转子截面轮廓渐开线、过渡曲线的参数方程表达式，并选择合适的参数取值范围；再利用“规律曲线”功能，即可生成高精度的函数方程曲线；

(2)画出相应的齿顶圆、齿根圆及必要的辅助线等；然后通过对相应曲线段和圆弧段的修剪、旋转调整至适宜位置、对称操作等，得到单个齿廓曲线，如图5所示；

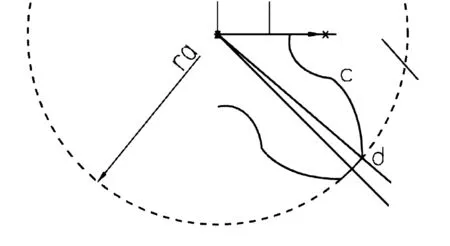
图5 在UG中所得的螺旋转子单个齿廓曲线

(3)通过阵列、修剪等操作，得到完整的转子截面轮廓。

(4)在此基础上，构建相应的空间螺旋线作为引导线，经扫掠操作即生成一个完整螺旋螺旋转子三维数字化模型。

用同样方法，可完成另一旋向相反的螺旋转子建模。

为验证上述建模设计方法及结果的合理性，通过UG软件对构建的螺旋转子数模进行运动仿真，如图6所示。利用UG的干涉分析功能，首先确认双转子运动过程中相互啮合的工作齿面无干涉；然后模拟双转子在压差作用下各自转动的效果。仿真结果表明，两转子在无干涉情况下，啮合运转能紧密且平稳持续地进行。

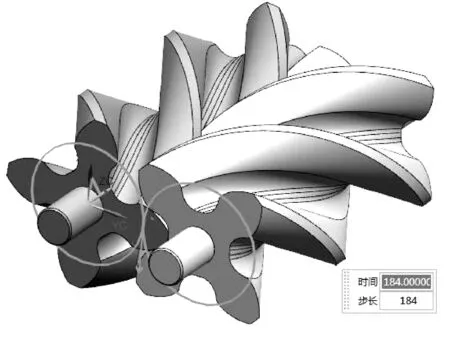
图6 双转子啮合运动仿真

3 螺旋转子零件的数控加工

3.1 数控加工原理

根据螺旋转子零件的形状结构特点，结合国内现有生产条件，宜采用四轴铣削加工中心，用标准球头铣刀进行加工。数控铣削的基本原理如图7所示，其中机床上的旋转工作台带动工件绕X轴旋转即实现A轴运动。加工时，工件沿X轴方向相对于刀具作均速直线进给，同时沿A轴作匀速旋转[9]，直线运动距离和旋转角度之间保持相应的比例关系，这样刀具即加工出一条空间螺旋线；然后工件快速复位，刀具在YOZ平面联动，快速运动到下一条螺旋线起始点，依次加工下一条螺旋线，直到完成整个螺旋面的铣削。

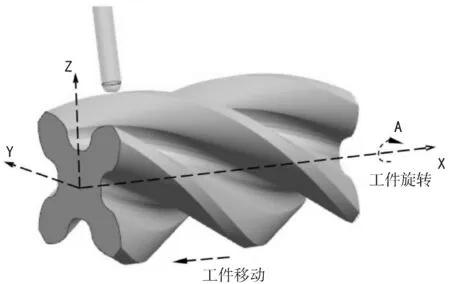
图7 标准球头铣刀数控铣削螺旋转子的原理

加工过程中，机床通过Y、Z 轴联动，可依次调整刀具相对于工件在轴向及径向的位置，这样可控制刀具在YOZ平面所到达的相应点位，从而由系列刀具切削点拟合组成转子的截面轮廓曲线；同时配合X、A轴联动加工出一条条螺旋线，由螺旋线组成螺旋面，实现螺旋转子的数控加工，其过程类似于“行切法”加工。

3.2 数控加工程序的编制

考虑到完全采用自动编程所生成的数控程序，其实质是沿每条加工路径用小直线段来逼近空间型面，与转子螺旋面的形成机理有一定差异，不利于精度提高；故采用手工编程结合自动编程的方法进行数控编程。[10-12]首先根据转子的数字模型，应用UG的CAM模块，通过设置相应的加工精度、刀轴矢量、干涉检查等，计算出铣削加工每条螺旋线时，刀具在螺旋线切削始点处的刀位点数据；然后按上述X、A轴联动加工螺旋线的原理，采用手工编程方法，并引入宏变量，以刀具在螺旋线切削始点处的刀位点数据对宏变量进行赋值，编写出空间螺旋线加工子程序，供主程序多次调用；这样大大简化了程序结构，精简了程序量，且易于修改。

编程时加工走刀路径的规划，可按照齿槽的形状，遵循由外而内、尽量左右对称的原则，即先分别加工转子一个齿槽左、右两边最外侧的型面螺旋线，然后刀具沿Y、Z方向联动进给一个切削行宽度，加工相邻的左右两条型面螺旋线；依次加工直至切削完成一个齿槽；接着A轴旋转90°，用同样方法加工下一个齿槽，直至完成全部加工。经宇龙多轴数控加工仿真软件的模拟运行及相关数控切削加工实验，表明该编程方法简洁高效，效果良好。转子零件数控程序部分代码如下所示：

O1006

G0 G54 Z100 G90

X-6.Y0

M03 S3500

#1=0

#2=81

#101=44.238

#102=56.029

M98 P8106

#101=44.148

#102=55.45

M98 P8106

………

………

4 结 语

本文分析了螺旋转子零件的型面轮廓形成原理，在此基础上推导求取了其截面轮廓曲线的函数方程，进而应用UG软件构建了其三维精确数模；采用自动编程结合手工编程，编写了螺旋转子的数控加工程序；通过相关实验验证了上述方法和结果的正确性。本文所提供的方法应用于企业实际，可较好解决现有生产条件下采用标准刀具加工螺旋转子的技术问题，具有一定的推广应用前景。