基于“θ”值法的民间金融规模测算——以合肥市为例

刘 炯，林峥峥

(1.宣城职业技术学院 旅游商贸系，安徽 宣城 242000；2.安徽外国语学院 国际经济学院，合肥 230000；3.合肥学院 经济与管理学院，合肥 230601)

0 引 言

学术界一般认为，民间金融是游离于正规金融体系之外的、未纳入国家金融当局管理的金融活动的总和，有时也称之非正规金融。由于民间金融自发产生，隐蔽性特征鲜明，不在官方统计领域之内，因而唯有凭借测算，方可获取它的规模。习见的方法有直接测算法和间接测算法，前者实质是统计学中的抽样调查法，通过对有代表性的样本的实地调查，推算出总体的民间金融规模。[1]间接测算法则是运用相关统计数据进行测算，主要有李建军的经济金融相关系数法和郭沛的资金供求轧差法。

2005年,李建军提出经济金融相关系数法，可以测算民间金融规模。[2]此方法把经济金融相关系数(投入产出比例)用“θ”表示。在实际应用中，常需要选择参照物计算出各年度“θ”的具体数值，所以又叫“θ”值法。运用该方法，彭芳春测算出1993—2009年武汉市的民间金融规模[3]，欧文测算出2000—2011年株洲市的民间金融规模[4]，宾伟华测算出2003—2014年岳阳市的民间金融规模等等。[5]已有的研究结果表明，“θ”值法比较科学，测算结果与真实值之间的差距不大，测算偏差也在可接受的范围之内，因此，“θ”值法具有较高的参考价值，被广泛应用于测算民间金融规模。

本文选用“θ”值法，测算合肥市2000—2018年的民间金融规模。选取民间金融规模指标与GDP指标分别代表合肥市民间金融发展与合肥市经济增长，使用EVIEWS9.0软件，计量分析合肥市民间金融对合肥市经济增长的影响。根据研究结论，为合肥市民间金融风险防范与规范发展建言献策，以期更好地发挥合肥市以及经济发展水平相当的地区民间金融对区域经济增长的促进作用。

1 合肥市民间金融规模测算

1.1 “θ”值法的基本假设

假设1：同一时期(一般为一年)全国各个地区存在相同的“θ”值。在市场经济高度发展的情况下，全国可以被看作是各个地区各种经济共同相处、相互依存的一个大环境，市场在资源配置中占据决定地位，资本和劳动自由流动，最终势必实现“等量的资本投入、劳动投入生产等量的产出”的均衡状态。不同年份的因素，比如经济政策、技术进步、创新等不同，相应的，经济运行的效率则有所不同。因此，一定时期内各地区资本对经济的贡献一致，即各地区在同一年份经济金融相关系数“θ”值相同，亦即资本投入与产出的比例相同，不同的年份资本与产出比例则有所不同，该假设的理论基础为分析投入与产出关系的道格拉斯生产函数。[6]

假设2：正规金融越发达，民间金融越式微。正规金融资源的缺乏为民间金融的生存提供了沃土，民间金融的存在弥补了正规金融的不足。正规金融越衰弱，民间金融越兴盛；正规金融越兴旺，民间金融的空间越狭窄。极端地，当正规金融足够发达，民间金融几无发展余地。北京市金融机构云集，金融制度完善，金融监管严格，民间金融举步维艰。故而，相对于庞大规模的正规金融，北京市的民间金融可以忽略不计。所以，可选取北京市作为测算合肥市民间金融规模的参照物。

1.2 “θ”值法的逻辑思路

根据“θ”值法的假设以及金融学理论，可得：

θ=FAi/GDPi=FAj/GDPj

(1)

FAi=FFi+IFi,FAj=FFj+IFj

(2)

其中，FA表示融资总量，即资本投入量，包括正规金融融资FF和民间金融融资IF两个部分，GDP表示国内生产总值，i与j分别表示i地区与j地区。

李建军教授的“θ”值模型中的正规金融由三部分构成：短期贷款、股票融资、外商直接投资[2]，即，

FA=STL+STF+FDI

(3)

公式(3)中，STL代表短期贷款，STF代表股票融资,FDI代表外商直接投资。

联立(1)、(2)、(3)三个公式，经过代数演算可得：

(4)

因此，只要选择一个正规金融高度发达的地区，比如北京，算出“θ”的具体数值，然后获取合肥市的短期贷款、股票融资、外商直接投资与国内生产总值的具体数值，对公式(4)稍作简单的代数变形即可计算出合肥市的民间金融规模。

1.3 合肥市民间金融规模的测算

“θ”值测算：根据“θ”值法的基本假设和逻辑思路可知，要想测算出合肥市的民间金融，首先选择一个金融高度发达的地区“θ”值作为参照。由前面假设可知，可以选择北京市的“θ”值为参照。从2001—2019年的《北京统计年鉴》，选取计算北京市“θ”值所需的相关年度的短期贷款、股票融资、外商直接投资和国内生产总值的数值，见表1。

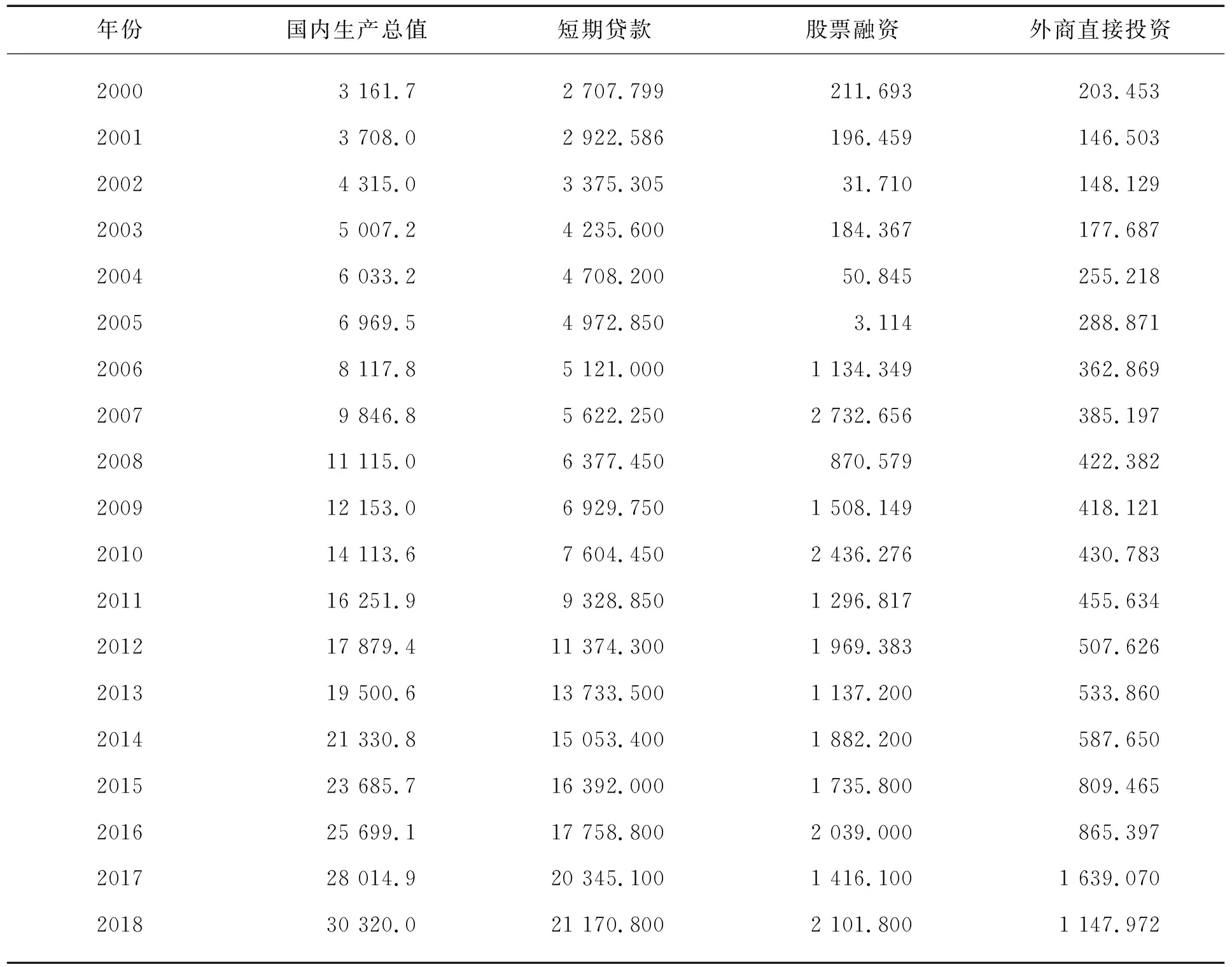
表1 北京市主要金融指标 单位：亿元

综合运用公式(1)、(2)、(3)，计算出北京市2000-2018年的经济金融相关系数“θ”的具体数值，参见表2。从计算结果可以看出，北京市各年度“θ”值的范围在0.682与0.988之间，平均为0.804。

表2 北京市2000—2018年“θ”值

合肥市民间金融规模测算：根据公式(4)，以北京市为参照物，测算合肥市民间金融规模，需要所测算各年度的短期贷款、股票融资、外商直接投资和国内生产总值的数值，所需数据皆来自于2001—2019年《合肥统计年鉴》，如表3所示。

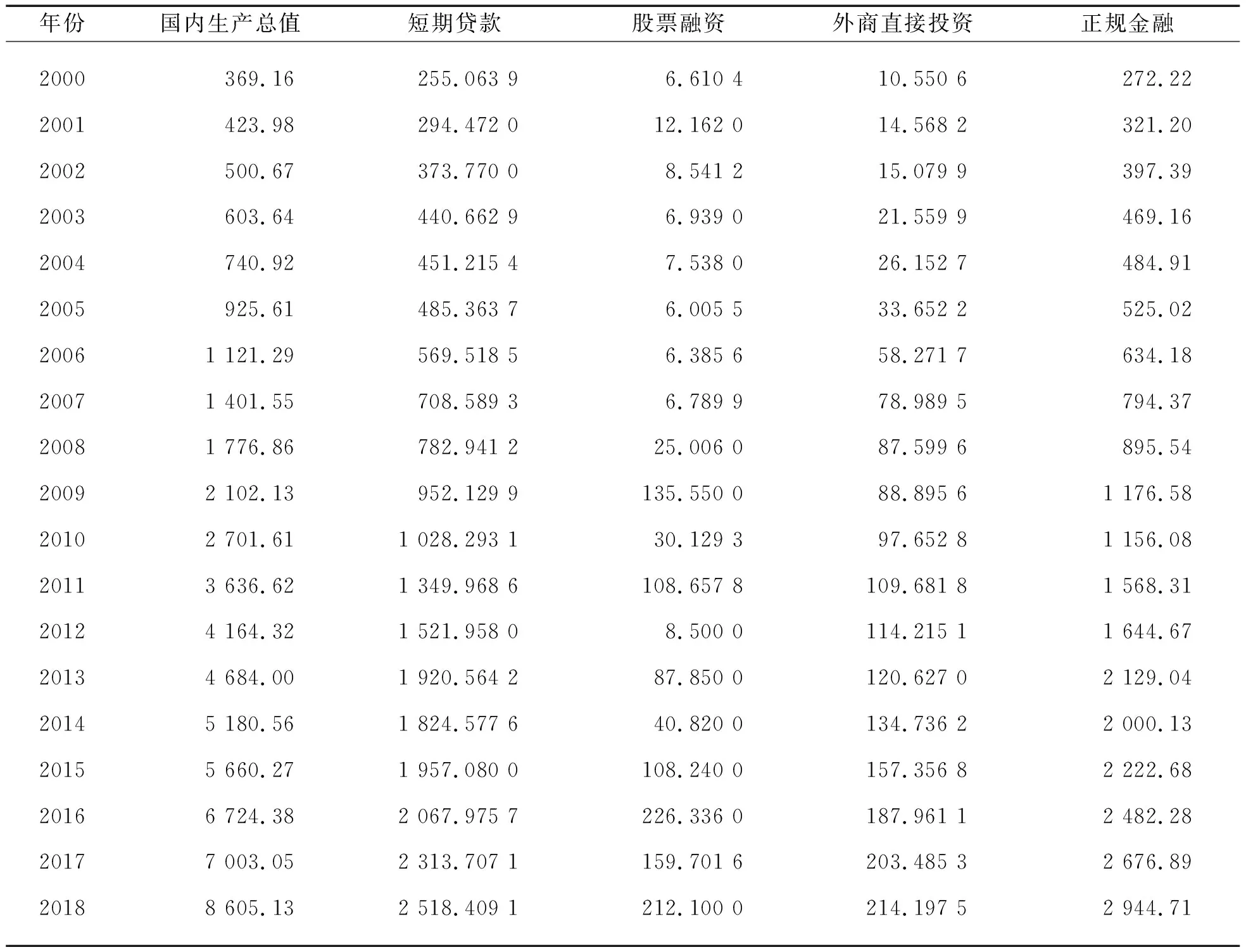
表3 合肥市主要金融指标 单位：亿元

由“θ”值法的基本假设和逻辑思路可得，合肥市民间金融规模计算公式如下：

IFj=θ×GDPj-(STLj+STFj+FDIj)

(5)

这里的IFj、GDPj、STLj、STFj、FDIj分别表示合肥市的民间金融、国内生产总值、短期贷款、股票融资、外商直接投资，运用公式(5)，计算出合肥市2000—2018年民间金融规模，见表4。。

表4 合肥市民间金融规模 单位：亿元

综合考察表3、表4，可以看出，2000—2018年内，伴随着合肥市经济的快速发展以及2011年合并县级巢湖市与庐江县，合肥的GDP迅猛增长，年均增长19.12%。与此同时，合肥市民间金融发展迅速，总体上的上升趋势十分显著，18年间共计增长了42.05倍，平均每年增长23.25%。

2000—2018年，合肥市正规金融增长了10.82倍，平均每年增长14.14%，远低于民间金融规模扩张速度。从绝对数来看，合肥市正规金融与民间金融规模不断扩大，2014年民间金融首次超过正规金融且有差距越来越大之趋势，由此可见，合肥市民间金融与正规金融共同发展，民间金融很大程度上弥补了正规金融的供给不足。

整个考察期内，民间金融规模有着两次较大的起伏，一次是从2000年的92.51亿元跌至2001年的21.37亿元，可能的原因是：受到911事件拖累，世界经济疲软，发展中国家跟着遭殃；另一次是从2007年的450.21亿元降到2008年的330.49亿元，主要是受到美国2008年次贷危机的影响。较大的规模且波浪式的上升趋势，意味着合肥市民间金融风险较大，势必增加民间金融的不确定性。

“θ”值法固然是一种间接测算法，不是非常的精确，但是其测算结果，却真实地反映了合肥市民间金融的大致情况：规模较大，与正规金融同步发展，呈现出波浪式上升趋势。

2 计量分析

2.1 指标与数据说明

民间金融指标，采用民间金融规模表示，记为IF，前文已经运用“θ”值法测算出2000—2018年各年度的合肥市民间金融规模。经济增长指标，学术研究习惯采用国内生产总值，本文沿袭惯例，用GDP表示，样本数据来源于《合肥统计年鉴》。民间金融与经济增长二者同为总量指标，因此不需要考量不同年份人口变动，也不需要剔除通货膨胀因素，因为人口与物价因素对二者均有着同样的影响。

2.2 计量分析

(1)平稳性检验。实际经济问题的时间序列大部分非平稳，如果不经过平稳性检验就直接进行回归分析，容易出现对非平稳变量伪回归问题。[7]

依据赤池信息准则以及施瓦茨最小标准确定最佳滞后期数，采用ADF检验法，对IF与GDP进行平稳性检验，检验结果见表5。三种检验形式下，IF与GDP的ADF统计量都大于10%临界值，P值均大于10%，不能拒绝原假设，因而IF与GDP都是非平稳序列；继而对IF与GDP的一阶差分DIF与DGDP进行单位根检验，可知DIF与DGDP在1%显著性水平下平稳，所以IF与GDP都是一阶单整序列。

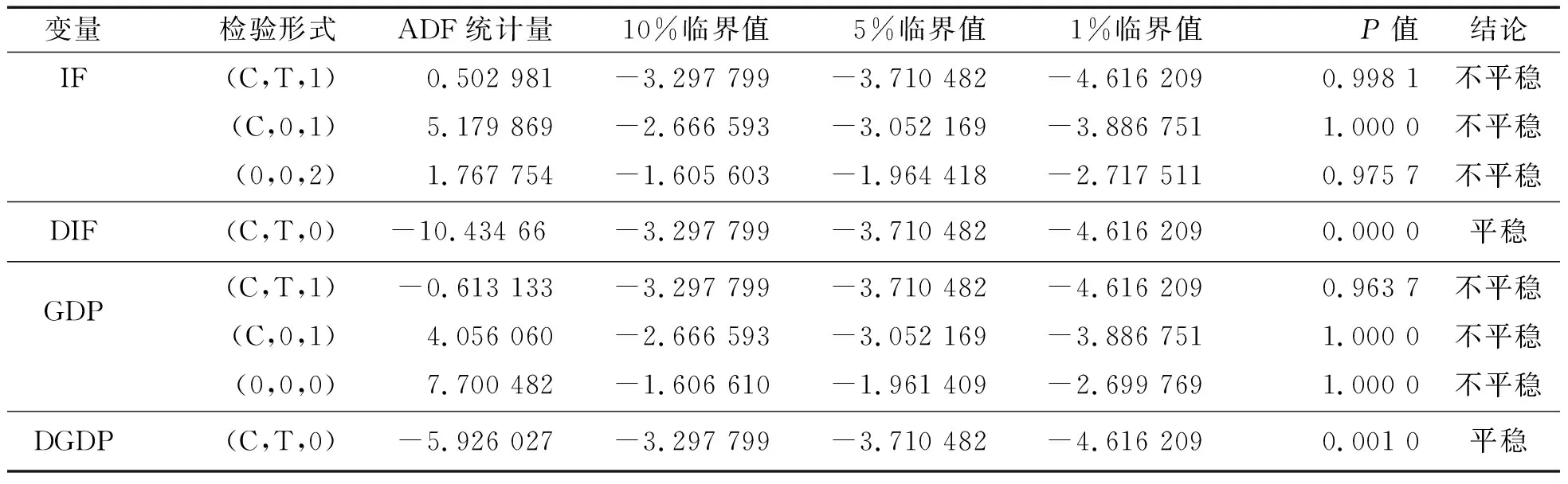
表5 LNIF与LNGDP单位根检验结果

(2)协整分析。单位根检验表明，合肥市民间金融序列IF与合肥市国内生产总值序列GDP都是一阶单整的，符合协整的必要条件，可以进行协整分析。本文选择E—G两步法对GDP与IF两个变量进行协整检验。

第一步：以GDP为被解释变量，以IF为解释变量，借鉴欧文[3]、冯曦明[8]、冯海红[5]等的做法，将模型设定为

GDP=α+βIF+e

(6)

运用普通最小二乘法实施回归分析，获得GDP与IF的回归方程：

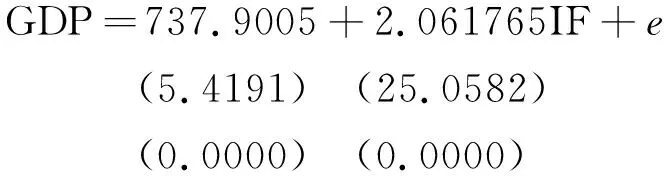
(7)

回归结果还显示，R2为0.973 640，调整的R2为0.972 089，F-stat高达627.914 8，P(F-stat)的值是0.000 000。

从回归结果来看，回归系数通过t检验，回归方程通过F检验，说明IF对GDP影响显著。因为R2和调整的 R2都很大，进而判断，方程(7)拟合程度很好。

第二步：由回归方程，可得

e=GDP-2.061 765IF-737.900 5

(8)

为排除伪回归，对残差e进行水平项的ADF检验。鉴于残差序列，所以采取不含常数项和趋势项的检验形式[9]，表6为检验结果。

表6 残差e的水平项单位根检验结果

由检验结果可知，残差序列的t统计量-2.778 636小于1%显著性水平的临界值-2.699 769，从而拒绝原假设，表明残差序列e不存在单位根，是平稳序列，说明GDP与IF存在协整关系，即合肥市经济增长与合肥市民间金融之间存在长期的均衡关系，IF每增长1个百分点，促进GDP增长2.061 765个百分点，合肥市民间金融正向影响合肥市经济增长。

(3) Granger因果关系检验。IF与GDP存在协整关系，但IF与GDP是否存在因果关系，尚需进行Granger因果关系检验，表7输出检验结果。

表7 Granger因果关系检验结果

检验结果表明，在5%的显著性水平下，拒绝“IF不是GDP的格兰杰原因”的原假设，不能拒绝“GDP不是IF的格兰杰原因”的原假设，因此，IF是GDP的格兰杰原因，GDP不是IF的格兰杰原因，IF与GDP存在单方向上的格兰杰因果关系，这与欧文[3]、冯海红[5]的研究结果保持一致。

3 结论与建议

3.1 结 论

本文所使用的“θ”值法假设条件相对苛刻，不完全符合我国实际的国情，在现实经济中难以实现，因而不能保证理论测算的结果完全正确。在无法获得准确数据的情况下，“θ”值法的测算结果却真实地反映了合肥市民间金融规模的基本状况、变化趋势与发展规律：发展较快，规模较大，有效地弥补了正规金融资源的不足；规模扩张起伏较大，呈现波浪式上升态势，风险十分明显。

协整检验揭示，合肥市经济增长与合肥市民间金融存在长期均衡关系，二者同方向变动，民间金融规模的增长显著地促进了GDP的增加。格兰杰检验表明，合肥市经济增长与合肥市民间金融存在单方向的格兰杰因果关系，民间金融显著地促进了经济增长，经济增长亦对民间金融发展产生一定的推动作用。

3.2 建 议

合肥市民间金融规模较大，受经济发展的影响较大，风险已然存在，需要关注和防范。一要加强民间金融研究，定期采集数据，把握其发展规律，预测其发展趋势，才能发现问题，防患于未然；二要设立监管机构，负责制定与民间金融相关的政策，实时监测民间金融的规模、利率、组织形式及其运营，有针对性地加强监督管理。三要向中小企业、农户、城镇居民等民间金融资金供需主体提供经济金融、法律专业知识咨询服务和培训，培养风险意识，树立法律观念，使得他们能够正确认识风险，以及在纠纷出现后知晓如何依法处置。四是要严厉打击非法集资、洗钱、带有黑社会性质的融资等扰乱市场经济的非法金融行为，整饬地方金融秩序，维护地方社会稳定。

计量分析表明，合肥市经济增长与合肥市民间金融存在长期均衡关系，合肥市民间金融显著地促进了合肥市经济增长。为此，应合理引导合肥市民间金融健康发展。一是加快相关政策法规的建设，确保民间金融的合法地位，确定民间金融的合法界限，确立民间金融合法运行，保护借贷双方的合法权益，并能够解决民间金融活动出现的各种问题与纠纷。二是在当前相关法制尚不健全的情况下，对于合情合理而又不违法的内生性民间金融活动，给其一片自由翱翔的天地，让其充分发挥金融对经济发展的促进作用。尤其鼓励民间金融资金支持中小企业，比如贷款、入股、担保或租赁，缓解中小企业融资难，促使其发展壮大的同时亦能够促进自身的繁荣，实现“双赢”。三是加强与正规金融的合作。在向农户与中小企业供给贷款时，民间金融的信息优势明显，手续更加灵活，而在管理与资金规模方面，正规金融的优势却非常的显然。该当发扬各自的比较优势，断长补短，协力同心地推动地方经济可持续发展。