基于结构张量的混合阶偏微分方程图像去噪
2020-11-14许宛如吴海峰
许宛如,刘 奎,吴海峰
(安庆师范大学 计算机与信息学院,安徽 安庆 246011)
0 引 言
图像在获取、存储和传输的过程中会引入噪声,这严重影响对图像的后续处理。因此,图像去噪一直是数字图像处理领域的研究热点。近几年来,随着数学理论的发展,偏微分方程(PDE)成为数字图像处理的主要工具。1990年Perona和Malik提出的基于偏微分的各向异性扩散模型(PM模型)[1]对图像恢复领域的工作具有着开创性,PM模型中的扩散系数采用在不同方向上梯度的单调递减函数,即在平坦区域梯度值较小,则它的扩散系数较大,可以平滑平坦区域的噪声;而边缘或角点区域梯度值较大,则其扩散系数较小,能保护边缘和角点。但这个模型在数学理论上被证明是“病态的”,即方程解的唯一性和稳定性得不到保证。此外,噪声的频率与图像边缘频率的相近,使得PM模型会把噪声信息误认为边缘信息,在平滑区域处减少扩散,产生“阶梯效应”(伪边缘)。1992年Rudin等人提出的全变分去噪[2],该模型以梯度信息作为图像平滑性的度量来实现图像去噪,由于该模型所依赖的是梯度范数,所以也会导致在图像的光滑渐变区域出现阶梯效应。通过增加扩散模型的阶数[3-8],利用分段斜面来逼近原始图像来克服“阶梯效应”是一种常用有效的方法。根据这个思想,2000年You和Kaveh两人首次提出了基于拉普拉斯算子的四阶偏微分方程图像去噪模型(YK模型)[3],该模型虽然能有效的消减阶梯效应,但是该模型在平滑区域滤波噪声时,会产生黑白斑点。
为了克服上述传统模型的缺陷,刘奎等人提出了基于结构张量的各项异性扩散模型[9],该模型很好的保护了图像的纹理细节,但是当噪声密度大时,去噪效果并不是很好。文献[5]提出了基于结构张量的四阶偏微分方程模型,该模型能很好的去除图像里的噪声,但是存在着边缘的模糊现象。本文综合了基于结构张量二阶偏微分方程和四阶偏微分方程的优点,提出了一种基于结构张量的混合阶偏微分方程模型。实验证明,本文模型能更好的在去除噪声的同时保护图像的边缘、纹理等细节。
1 非线性扩散模型
1.1 各向异性扩散模型
在图像去噪的早期,最先用于图像去噪的是各向同性线性热扩散模型,这种模型的优点是速度快,在平滑区域能很好地去除噪声,但是该模型不能有效保护边角。为了克服热扩散模型的缺陷,Perona与Malik首次提出的保持边缘各向异性扩散模型[1],该模型是传统热扩散模型的一个推广,其形式为:
(1)
其中u0是原始图像,u是噪声图像,div是散度算子,u是u的梯度,|u|是u的梯度模,g(•)是一个非负增函数,作为扩散算子,当g(•)=1时,该模型退化为各向同性热扩散方程。g(•)有两种经典形式如下:
(2)
其中k是一个常量。
1.2 四阶偏微分模型(YK模型)
为了消除PM模型的缺陷,2000年You和Kaveh两人提出了基于拉普拉斯算子的四阶偏微分方程图像去噪模型(YK模型)[3],来实现去噪和保留边缘之间的权衡。该模型的能量泛函:
(3)
(4)
(5)
其中k>0是拉普拉斯阈值。YK模型使用Laplacian算子代替梯度算子,利用分段斜面来逼近原图的,有效地克服了“阶梯效应”。但是该模型在平滑区域滤波噪声时会产生斑点,影响去噪图像的视觉效果。
2 基于结构张量的偏微分方程
1897年DiZenzo提出了的结构张量的概念,结构张量可以用于提取和分析图像的局部结构信息,如几何结构和方向。近些年,结构张量已经在数字图像处理和机器视觉领域中得到了广泛应用[10-14]。结构张量的定义如下:
(6)
其中Gρ是标准差为ρ的高斯核函数,*是卷积运算符,uσ是图像u经过方差为σ的高斯滤波图像,即uσ=u*Gσ,目的是使边缘检测对尺寸小于σ的内容不敏感,从而提高边缘检测的鲁棒性。结构张量矩阵Jρ是一个对称的半正定矩阵,其两个正交的单位特征向量如下:
(7)
特征向量v1和v2分别用来表示边缘的法线和切线方向,用来控制扩散方向。它们对应的两个非负特征值如下:
(8)
通过结构张量的两个特征值来计算它的行列式d(d=λ1×λ2)和迹t(t=λ1+λ2),特征值λ1,λ2能反映图像局部的特征信息,在平滑区域,λ1≈λ2≈0,对应d≈t≈0;在边缘区域,λ1>>λ2≈0,对应d≈0,t>>0;在角点区域,λ1≈λ2>>0,对应d>>0,t>>0。
使用结构张量的行列式和迹来构造扩散系数,刘奎等人提出了基于结构张量的自适应各向异性扩散模型[9],该模型能很好的克服传统PM模型的缺陷,模型如下:
(9)
其中,η和ξ分别表示等照线方向和梯度方向,u0为噪声图像,阈值K>0。该模型充分发挥了结构张量的优势,保护了图像的边缘纹理,但是当噪声严重时,不能有效去噪。
文献[5]将结构张量与四阶偏微分方程结合提出了基于结构张量的四阶偏微分模型,模型如下:
(10)
其中,v1v1和v2v2分别表示结构张量估计的梯度方向和边缘方向,阈值K用于边缘保持,可手动设置。 在式(9),(10)中方程的前两项是扩散项,第三项是保真项,λ是拉格朗日乘子用来平衡数据项和保真项。
3 基于结构张量的组合PM模型和四阶YK模型
3.1 混合偏微分模型
受文献[8]和文献[9]启发,本文提出了一种基于结构张量的混合阶偏微分模型,如下:
(11)
在二阶偏微分模型使用局部坐标系(ξ,η),其中ξ代变梯度方向,η代表对应的垂直方向;在四阶偏微分模型引入局部结构张量坐标系(v1,v2),其中v1代表梯度方向,v2代表边缘方向,则模型如下:
(12)
其中d是结构张量的行列式,t表示结构张量的迹,uηη和uξξ分别表示图像在梯度和水平集方向上的二阶导数;uv1v1和uv2v2分别表示图像沿着由结构张量估计的梯度方向和边缘方向的二阶方向导数,计算如下:
(13)
模型的扩散系数g(h)的大小,决定于结构张量的行列式和迹。在图像平滑区域,d≈t≈0,则g(d)≈g(t)≈1,在梯度方向和其垂直方向上的扩散程度几乎相同,能有效去噪;在图像边缘区域,d≈0,t>>0,则g(d)≈1,g(t)≈0,扩散只沿着边缘方向,在梯度方向上几乎不扩散,能很好的保护边缘和细节;在图像的角点区域,d>>0,t>>0,则g(d)≈g(t)≈0,此时,在角点处不扩散,起到很好的保护角点的作用。
3.2 模型求解
使用有限中心差分法对本文提出的模型(11)进行求解,对于二维图像u的一阶和二阶导数如下:
(14)
(15)
(16)
(17)
(18)
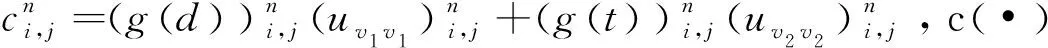
(19)
(20)
4 实验结果与分析
为了评估提出模型的有效性,进行大量实验,选取了合成图像、512×512的Lena图像Barbara图像和Pepper图像作为仿真实验的测试图。将本文改进模型分别与PM模型[1]、张量PM模型[8]、和张量YK模型[9]分别对加噪图像进行滤波处理。图像去噪中对滤波器性能的评估从主观评价和客观评价两个方面从发,客观评价的标准采用峰值信噪比(PSNR)、信噪比(SNR)和平均结构相似性(MSSIM),分别定义如下:
(21)
(22)
(23)
其中u和u0分别表示去噪后的图像和原始图像,M、N分别为图像的高度和宽度,μu、μu0分别表示图像u和u0的均值,σu、σu0分别表示图像u和u0的方差,σuu0表示图像u和u0的协方差,H表示滑动窗口将图像分成H块。SNR和PSNR数值越大表示图像失真越小;MSSIM取值范围为[0,1],数值越大表示图像失真越小。
在实验中,基础参数设置λ=0.9,α=0.55,Δt=0.35。对Lena和Peppers图像添加标准差为20(σ=20)的高斯噪声,给合成图和Barbara图像添加标准差为30(σ=30)的高斯噪声,实验结果主观效果如图1~图5,图中(a)是原始图像,(b)是噪声图像,(c)是PM模型去噪图像,(d)是PM模型去噪图像,(e)是张量YK去噪图像,(f)是张量YK去噪图像,(g)是本文模型去噪图像。客观数据对比如表1~表2。
由图1(c)、图3(c)、图4(c)和图5(c)可以看出,经PM模型处理后的图像会在边缘产生模糊的现象,结合图2(c)的局部放大图,可以看出图像去噪效果不显著且产生现阶梯效应;由图1(d)、图3(d)、图4(d)和图5(d)可以看出,经YK模型处理后的图像去噪效果明显,但结合图2(d)的局部放大图,可以看出图像平滑过度,损失大量边缘细节且会产生黑白孤立的斑点。

(a)原始图像

(a)原始图像

(e)张量PM模型

(a)原始图像

(e)张量PM模型

(a)原始图像

(a)原始图像
由图2(e)和其他个图(e)可见,张量PM模型处理后的图像去噪效果有提高,但存在着边缘细节被模糊和丢失的现象。由图2(f)和其他个图(f)可见,张量YK模型处理后的图像去噪效果显著,但处理后的图像过于平滑,使得部分边缘纹理模糊。最后比较图1(g)、图3(g)、图4(g)和图5(g),可见本文模型处理后的图像相比于前面模型,视觉效果更好,图像中的噪声得到了有效的抑制,且边缘和纹理也得到了有效保护,如图2(g)Lena图像的帽檐上的毛发细节、图4(g)合成图像中间十字没有模糊和阴影,而其他几种模型处理后的十字都有阴影。表1给出了噪声方差为20的Lena和Peppers图像使用各种模型算法去噪结果的PSNR、SNR和MSSIM指标比较,表2为噪声方差为30的合成图和Barbara图像使用各种模型去噪结果的PSNR、SNR和MSSIM指标的比较,由表1和表2中的数据可以得出本文模型处理后的图像峰值信噪比、信噪比和平均结构相似性均有显著的提高。
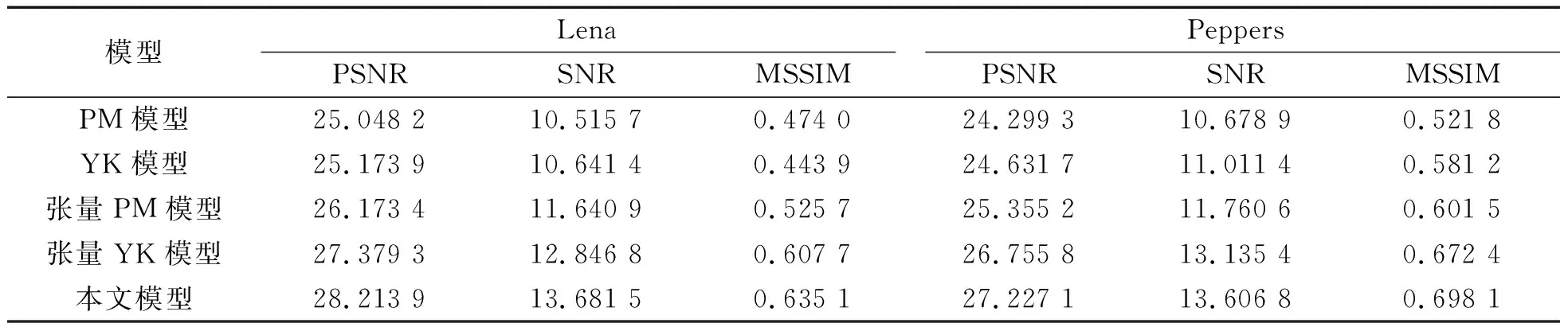
表1 Lena和Peppers图像各种模型去噪的PSNR、SNR、MSSIM的比较
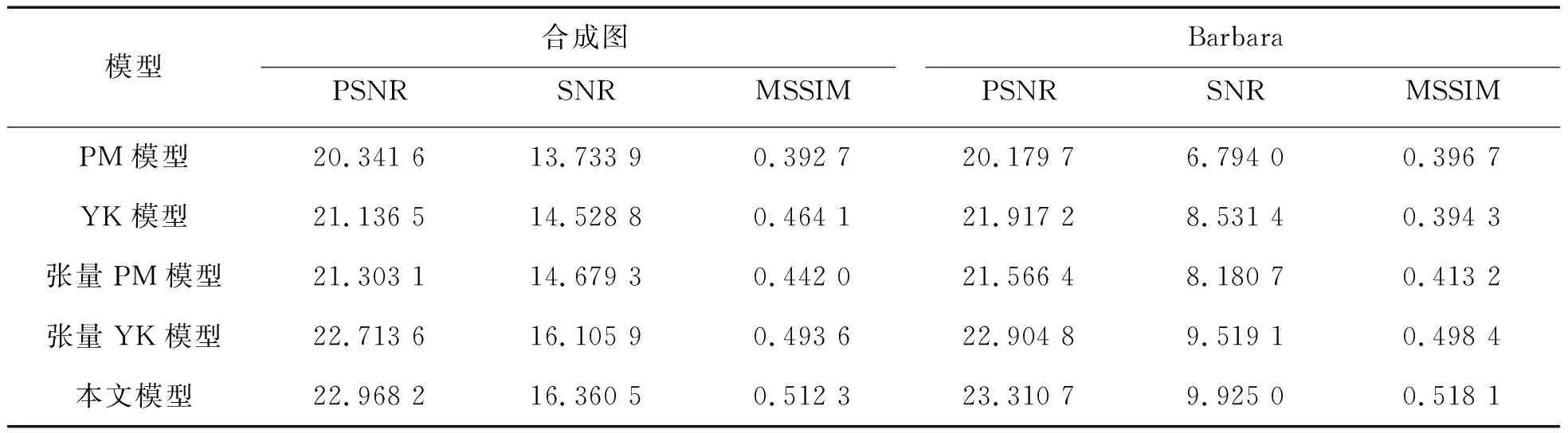
表2 合成图像各种模型去噪的PSNR、SNR、MSSIM的比较
5 结束语
提出一种基于结构张量的混合阶偏微分方程的图像去噪方法,该方法充分利用结构张量在确定图像边缘、角点的优势,分别在不同区域对其进行不同程度的扩散,达到在去除图像噪声的同时实现对边缘细节的保护。本文同时使用梯度坐标系和结构张量梯度坐标系,更加精准化的控制扩散。通过实验得出,将本文模型与PM模型、YK模型、张量PM模型、张量YK模型进行对比,本文模型去噪效果更显著,且更好的保护了图像的边缘特征和纹理细节。
