一种完全数据驱动的众数回归模型估计方法

李胜男，杨联强，潘东辉，沈 燕

(安徽大学 数学科学学院，合肥 230601 )

0 引 言

经典的均值回归、中位数回归和分位数回归模型分别估计条件分布的期望、中位数和分位数这些数字特征。但是，当数据的分布是多峰、重尾、有偏或存在离群值的情况下，这些模型的表现往往不够让使用者满意，尤其在稳健性方面表现不足。当今大数据时代，数据结构日益复杂，噪声源也形式多样，其分布往往远离经典情形下的正态性假定，此时，模型的稳健性就非常重要。因此，近年来流行的众数回归模型因其稳健性而被人们所关注，并且被成功的应用到实际问题研究中，例如温度数据的分析和预测[1]，交通工程的速度流分析[2]，阿尔茨海默症[3]的预测等。

而关于众数估计的理论研究，最早可以追溯到20世纪60年代 Parzen[4]的开创性工作，该方法给出的帕森窗方法为核密度估计和众数估计拉开了帷幕。而关于众数回归方法的研究，由Sager和Thisted[5]首次提出参数众数回归模型，然后Collomb[6]得到该估计量的一致收敛性质；Lee[7]用0-1损失函数得到了众数回归估计量并证明了其强一致性；Wharton[8]等人提出了估计局部条件众数的方法；Herrmann和Ziegler[9]通过核密度估计研究了密度函数众数的非参数估计问题；Einbeck和Tutz[10]给出了一种改进的MS(Mean Shift)算法来进行众数回归模型的估计；Yao[11]提出了一种非参数回归模型中回归函数的局部众数估计方法；Yao和Li[12]则研究了局部线性众数回归模型的理论性质；Sasaki[13]应用MS算法提出了通过直接估计对数密度梯度来寻找众数实现聚类；Chen[14]则对非参数众数回归模型的解在流形意义下给出了深刻的研究；Chen[15]也对众数估计及众数回归模型的研究历史和现状进行了全面的总结。

上述这些解法大都依赖于核密度估计，通常是借助核密度估计得到联合或条件密度函数，然后使用只有在核函数取高斯核时才可以得到的梯度上升迭代解法。但是，正如Sasaki[16]指出，这些方法将囿于核密度估计的原理，存在边界效应差、非全局最优、效率低等缺陷，而且一个效果好的密度估计方法并不一定是效果好的密度导数估计方法等。于是他们提出了一种直接估计对数密度导数进而估计条件众数的方法。本文则提出一种完全由数据驱动的众数回归模型估计方法，该方法从众数的本质特征出发，通过搜索最优覆盖区间，来确定条件众数。整个过程不依赖于核密度估计，也不依赖于梯度上升算法。在模拟和实际应用中，该方法表现良好，计算过程简洁，估计效果优良。本文内容结构如下：第一节给出众数回归模型理论及PMS算法简介，第二节提出一种新的完全由数据驱动的众数回归模型估计方法，第三节和第四节将分别给出模拟实验和真实数据应用结果，第五节对该方法进行总结。

1 众数回归模型的PMS算法简介

设有随机向量(X,Y)，其密度函数为p(x,y)。众数回归模型是估计在给定输入变量X的条件下输出变量Y的密度函数p(y|x)的众数，即回归函数M(x)=Mode(Y|X=x)，假设M(x)存在且唯一，等价的，

进一步，在X=x固定时，也等价于

给定观测值(xi,yi),i=1,...,n.众数回归函数估计流行的PMS(Partial Mean Shift)算法[2]是基于核密度估计和梯度上升的一种方法，本质上是MS算法在条件众数估计上的推广，具体实现可分成两个步骤：首先，用核密度估计表示联合密度：

这里m表示归一化常数，K表示核函数，hx和hy为带宽。其次，将核函数取为高斯核，‖•‖表示欧式范数，则由上式关于y的一阶条件可以得到如下迭代关系式：

(1)

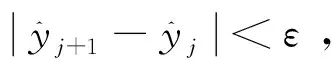
由上述过程可知，PMS算法的原理是基于核密度估计以及梯度上升迭代法得到条件众数的估计量。因此，该方法必然蕴含上节所述的源于核密度估计和梯度上升迭代法的缺陷。

2 完全数据驱动的众数回归模型估计方法

从众数的本质属性出发来解释本文给出的众数回归函数的估计方法。众数回归函数刻画的是在给定X=x时，随机变量Y的密度函数的最大值点M(x)，也就是说，此时，随机变量Y以最大的概率取值M(x)。因此，从实验观察的角度来看，此时应该有最多频数的Y观测点出现在M(x)附近。直观上来刻画这种现象，就是在X=x附近，如果将一个恰当的固定长度的小区间，沿着平行于Y取值的方向移动，当小区间中心位置移动到M(x)时，该小区间对观测值Yi有最大的覆盖率。根据这种众数回归函数的本质属性的直观解释，我们构造完全由数据驱动的众数回归模型的解法如下。

在给定的x处，首先，我们选定一个带宽hx，并以区间[x-hx,x+hx]来刻画x附近，再选定一个带宽hy，构造d个长度为2hy的区间Dj=[mj-hy,mj+hy]，其中

(2)

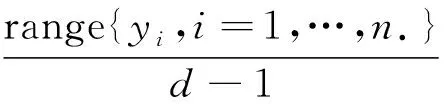
(3)

这里I(·)是示性函数。

(4)

现给出以上过程中超参数的选取法则。理论上，通过多重交叉验证法则来进行超参数选取，可以取得更令人满意的估计效果，但在实际应用中，特别是数据量较大和超参数个数较多时，交叉验证选取法则要付出巨大的计算成本。因此，所谓的经验法则(拇指法则)在实际应用中被频繁使用。本文方法所用到的超参数hx,hy和d选取经验法则如下：

(5)

其中[•]表示取整函数。

至此，将完全数据驱动的众数回归函数估计方法总结如下，

step1. 按(5)计算超参数hx,hy和d的取值;

step2. 按(2)计算mj,j=1,...,d;

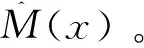
3 模 拟

首先，通过三个模拟来展现完全数据驱动的众数回归模型估计方法的拟合效果，并与PMS算法拟合效果进行比较，在每个例子中超参数选择按照上一节介绍的准则来进行，拟合效果图分别见图1、2、3。

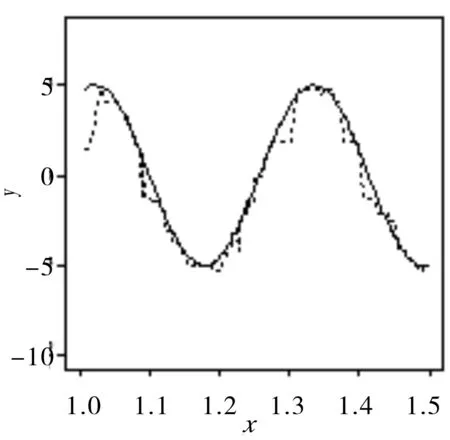
例1根据函数yi=5sin(20xi)+εi生成数据，样本xi从均匀分布(1,1.5)中抽取，样本容量为200，εi从均值为0，方差为0.5的正态分布中抽70%的样本点，从均值为-3，方差为0.5的正态分布中抽30%的样本点，估计效果图见图1。

(a)

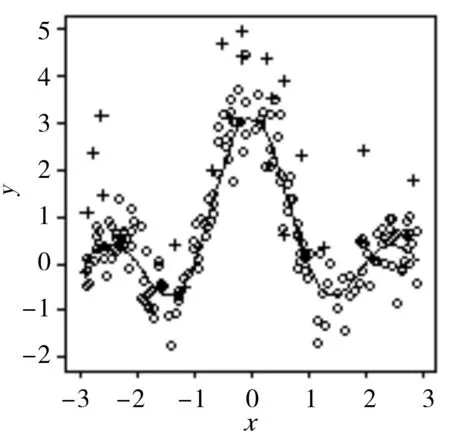
例2根据函数yi=sin(πxi)/xi+εi生成数据，样本xi从均匀分布(-3,3)中抽取，样本容量为200，εi从均值为0，方差为0.5的正态分布中抽取90%的样本点，剩下10%从均值为1，方差为1.5的正态分布中抽取，作为混入的离群点，估计效果图见图2。

(a)

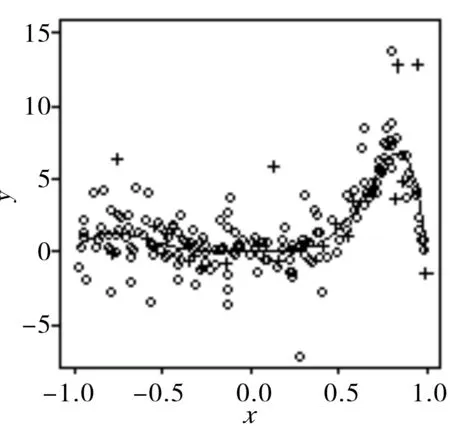
例3 根据函数yi=-20xi4(xi2-1)exp(xi)+εi生成数据，样本xi从均匀分布(-1,1)中抽取，样本容量为200，εi从自由度为4的t分布中抽90%，剩下10%从自由度为1的t分布中抽取，作为混入的离群点，估计效果图见图3。

(a)

从图3中可以看出，本文提出的完全数据驱动的众数回归模型估计方法可以很好的刻画出数据的原本特征，估计效果良好。本文还将PMS算法与完全数据驱动的众数回归模型估计方法做了简单对比，发现两者所用时间在参数选取适当的时候并没有太大差别，效果也并无太大差别，因此在只利用样本点，不借助任何工具的条件下完全数据驱动的众数回归模型估计方法更有优势。另外，见例2和例3，分别在数据中随机混入离群点。此时，我们知道通常的均值回归模型的表现会较差，受离群点影响很大，但由图2和图3中的(b)、(c)可以看出，众数回归模型依旧可以拟合出贴近真实图像的曲线，由此也验证了众数回归模型确实具有较好的稳健性。

4 应用

本节将完全数据驱动的众数回归模型估计方法应用于真实数据：加利福尼亚州不间断高速公路3车道速度流(数据来源见参考文献[2])。数据中包含1 318个样本，以流量作为自变量，速度作为响应变量，估计结果见图4，由图4可以看出完全数据驱动的众数回归模型估计方法拟合效果良好。

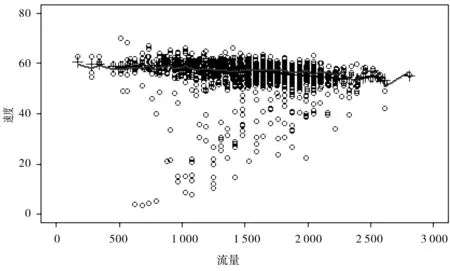
图4 加利福尼亚州不间断高速公路3车道速度流散点图.完全数据驱动的众数回归模型估计方法拟合函数(实线),PMS算法拟合结果(加号).

5 总结

基于对PMS算法的新理解，提出了完全数据驱动的众数回归模型估计方法，从数据本身出发，充分利用所给样本数据，不借助核密度或任何外部条件来进行拟合估计，做到完全由数据驱动。从上面的三个模拟实验以及真实应用中也可以看出这种算法拟合出来的曲线跟真实曲线差别并不大，表现良好。希望在后续的研究中可以继续挖掘这种方法的其他优点并且推广到实际应用中。