粘贴钢板法加固桥梁可靠度分析

曹智骅，杨林恺

(江西省公路科研设计院有限公司，南昌 330002)

0 引言

我国部分现役桥梁修建于20世纪80年代，随着社会经济的发展，超载等现象增加，服役桥梁结构也相继出现各种病害，桥梁的维修加固作为提高既有桥梁通行能力、缓解通行压力的重要的方式之一，已经被众多国内外学者作为研究对象。利用可靠度指标来量化加固处理后的桥梁使用寿命，定量评价加固方法与加固效果，对桥梁工程养护部门的决策是具有一定参考价值的。

目前国内外关于加固后的桥梁可靠度研究主要围绕承载能力极限状态可靠度分析进行评估，对于正常使用状态下的研究并不多。江胜华[1]等人对采用CFRP布加固的钢筋混凝土梁进行正常使用极限状态下可靠度表达式的推导，并对蒙特卡罗法可靠度分析法进行了改进；冯浩雄[2]等人对加固后的混凝土桥梁数据进行采集，采用JC法对结构可靠度进行计算，并对影响混凝土强度的各种因素进行了参数敏感性分析；胡建林[3]等人根据服役期间桥梁的实测数据，以桥梁时变可靠度作为判别指标，维修方案作为变量，对维修方案决策收益差异进行讨论分析；K.C.Chou[4]提出根据外观检测、材料试验以及非破坏试验等手段得到的数据，用模糊数学理论来对维修加固后的房屋结构的可靠性进行分析；Val[5]等人研究了采用外套纤维布加固柱体结构的结构可靠度，采用蒙特卡罗法对模型的材料强度、截面尺寸、恒活载比的参数敏感性进行了分析，得到三个参数的影响规律。

对加固后的桥梁进行正常使用阶段的可靠度评估，可以揭示加固后桥梁的日常服役性能，是保证桥梁结构在使用运营期间的必要条件，也可为后续维修加固方案的可行性分析进行指导。

1 粘贴钢板法

桥梁维修加固的手段是对既有的桥梁构件的补强，由于存在受力阶段的时间差，其加固设计方案较新建桥梁更为复杂，且对于耐久性有更高的要求。改善或维持原桥受力状态，不改变原桥的社会影响与投资效应，桥梁维修加固是较好的手段。

粘贴钢板法通过双组份环氧粘合剂粘贴砼外表面，形成互相结合的体系，其加固效果主要取决于衔接面传递应力的效果。通常的方法是采用环氧树脂系列材料，将钢板粘贴在受拉力部分的薄弱部位，与之形成整体，以钢板代替需要增设的钢筋，对梁体的承载能力进行补充，属于一种非破坏式的加固手段。在加固方案前，需对既有结构的受力现状和承载能力富余情况进行分析，以保证其加固后的结构体系传力线路明确，体系可靠。

图1 粘贴钢板法加固桥梁

2 蒙特卡洛法

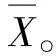
假设样本中有X1,X2,…,Xn，n个随机变量，其分别对应的概率密度函数为fx1(x1)，fx2(x2)，…，fxn(xn)，由n个随机变量组成的结构功能函数为Z=Fx(X1,X2,…,Xn)。重要性结构的失效概率可由下式进行计算，采用Matlab工具箱功能进行计算模拟分析：

(1)

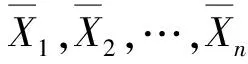
3 粘贴钢板法加固桥梁时变可靠度分析

3.1 抗力时变因素影响

3.1.1 混凝土强度

桥梁混凝土的强度服从正态统计分布，其经过t年后混凝土强度均值发展规律的时变统计模型如下式所示[6]：

μf(t)=η(t)μf0

(2)

式中:μf0是混凝土28d立方体抗压强度的均值；η(t)是均值时变函数，经回归分析得到其规律表达式为：

η(t)=1.4529exp[-0.0246(lnt-1.7154)2]

标准差可以表示为：σf(t)=ζ(t)σf0

式中:σf(t)是混凝土28d立方体抗压强度的标准差；ζ(t)是标准差的时变函数，经过回归分析得到其规律式为：ζ(t)=0.0305t+1.2368。

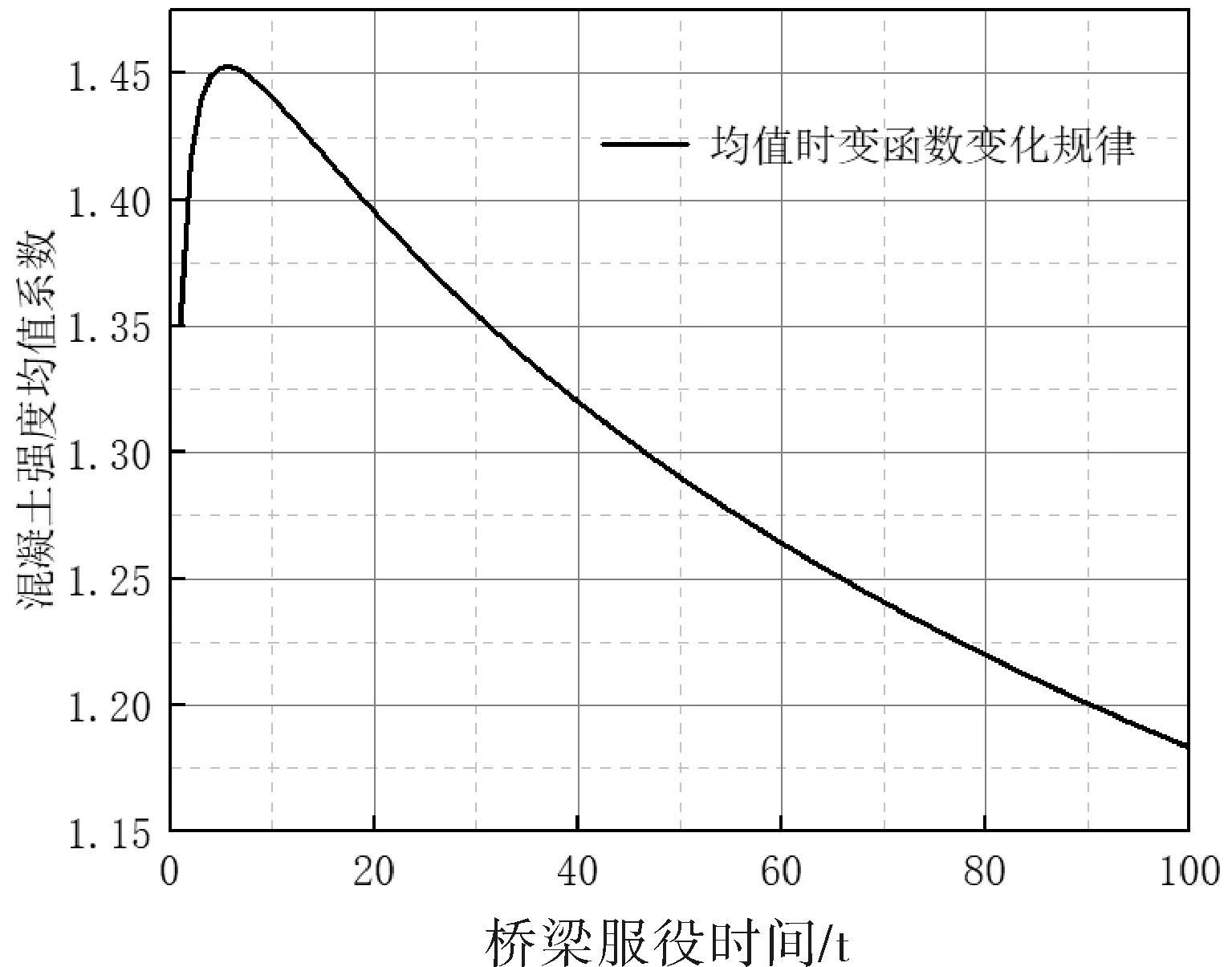
图2 混凝土强度均值时变函数规律

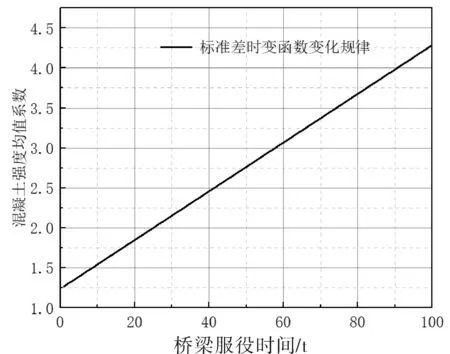
图3 混凝土强度方差时变函数规律

3.1.2 钢筋锈蚀截面

钢筋锈蚀的过程较为复杂，其影响多具有很大的随机性，根据相关参考文献[7]得到钢筋截面的损失率时变公式为：

η(t)=ω(t-t0)

(3)

(4)

(5)

式中：η(t)—对应t时刻的钢筋截面损失率；

ω—钢筋截面损失率函数；

t0—开始发生腐蚀的时间，为简化计算取桥梁服役时间；

c—钢筋混凝土保护层厚度(cm)；

d—钢筋的公称直径(mm)；

β1—混凝土养护系数,取1.0；

β2—水泥类别影响，对于普通硅酸盐水泥取1.0；

β3—环境作用系数，取1.34。

3.1.3 钢筋锈蚀屈服强度

钢筋在发生锈蚀时不但截面发生变化，钢筋力学性能也发生变化，主要表现为屈服曲线屈服阶段缩短、塑性能力变差、屈强比指标增大。当截面锈蚀率在15%以内时，名义屈服强度的标准值按下式表示[7]：

fsk=fk(1-1.077ηb)

(6)

式中：fsk—钢筋设计屈服强度；

fk—钢筋设计标准值；

ηb—截面锈蚀率。

3.2 荷载

3.2.1 恒载可变性参数

对于小跨径桥梁来说，恒载属于设计荷载的主要部分，一般来说随时间的变化较小，通常认为其服从正态分布规律，其概率分布和统计参数可直接表示为[8]：

(7)

μG=KGGk

(8)

σG=μGδG

(9)

式中：Gk—恒载设计值；

μG，σG—桥梁恒载的均值和标准差。

KG，δG—统计参数。可以直接引用国标工程可靠度规范值，结合桥面铺装和构件自重的正态统计参数，组合后的统计参数为KG=1.0148，δG=0.0431。

3.2.2 汽车荷载可变性参数

车辆荷载是一个与时间有关的变量，在整个桥梁服役过程中是动态可变的。由于缺少足够多的实测资料，本文按设计时的荷载统计特性进行推算，采用规范推荐的标准车辆荷载计算的效应值来进行既有桥梁的可靠度分析。

表1 车辆荷载计算参数统计分布规律

注：SQK表示汽车荷载作用下结构产生的效应值,FM(x)为汽车荷载效应的截口分布概率。

桥梁设计基准期T=100，t表示现阶段服役年限，汽车荷载效应的时变均值与标准差模型如下式所示：

μSQ(t)=μSQ(T)+[ln(t/T)]/αt

(10)

σSQ(t)=σSQ(T)

(11)

(12)

式中:μSQ(t)和σSQ(t)分别表示任意时间汽车荷载效应值的均值与标准差；σSQ(T)与σSQ(T)分别表示T=100年时汽车荷载效应的均值与标准差。αT为中间参数。

4 工程实例

以某30m简支预应力混凝土桥梁为例，现阶段桥梁的服役期为30年，桥梁的原设计荷载为汽-13、拖-60。随着社会经济的发展，需求荷载等级为城B，对应桥梁汽车荷载为一般运行状态。采用粘贴钢板的方法来对既有桥梁结构进行加固，以收集到的检测报告数据作为参数取值依据，对该桥的正常使用阶段能力进行判断。根据现行国标，受弯构件挠度为：

(13)

式中:l0为桥梁计算跨度；Bl为构件受弯长期刚度;Ms表示短暂荷载组合计算得到的弯矩值。

以桥梁跨中结构的挠度值f与规范允许的挠度值[f]两者的差值，建立桥梁结构正常使用极限状态下的可靠度方程：

Z=[f]-αf·f

(14)

式中:[f]为规范规定桥梁跨中的最大允许挠度；f为桥梁结构在恒活载作用下跨中截面的挠度值；αf为挠度计算模式的不确定系数，本文取1.1。

建立的可靠度方程的均值和标准差模型，依据误差传导公式，可推导如下：

(15)

(16)

根据现状桥梁检测资料分析结果，截面锈蚀率ηb取0.1。《城市桥梁检测与评定技术规范》CJJ/T 233-2015表5.4.1-1规定梁桥主梁跨中挠度限值为L/600，L表示为简支梁的计算跨径，跨中限值为μf=5cm，σf=0.105。考虑抗弯失效模式，其梁体跨中的挠度为μf=3.75cm，σf=0.234。设计基准期为100年，后续该桥梁的服务年限为70年。采用蒙特卡罗法计算后续服役期内加固时变可靠度，荷载仅考虑结构恒载以及汽车活载，采用Matlab工具箱进行可靠度计算，结果如图4所示。

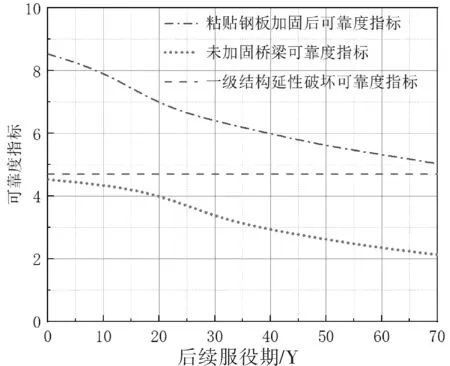
图4 粘贴钢板法加固桥梁前后可靠度指标计算

计算结果表明，加固后的桥梁在后续服务70年内目标可靠度可以满足使用阶段的要求，若不进行加固则桥梁不满足一级结构等级延性破坏可靠度指标要求，采用粘贴钢板加固法对既有桥梁进行加固是有效的。

5 结论

时变可靠度分析理论作为一种量化桥梁剩余服役使用年限指标理论，在桥梁使用寿命分析中得到广泛应用。以某30m简支预应力混凝土梁桥为例，对采用钢板加固后的桥梁混凝土强度、钢筋锈蚀截面、钢筋锈蚀屈服强度抗力时变统计参数进行分析，给出各参数的统计分布规律。对桥梁设计基准周期内的恒载时变分析参数、汽车荷载时变参数进行分析，在考虑恒载和汽车活载作用下利用粘贴钢板法进行桥梁结构加固正常使用极限状态下挠度计算公式的可靠度方程。

依据规范规定的一级结构延性破坏的可靠度限值，对桥梁剩余寿命进行判别。计算结果表明：在以挠度作为桥梁剩余使用寿命的评估方式中，采用钢板加固可以显著地增加桥梁的剩余使用寿命。