宽厚板矫直机支承辊强度分析
2020-11-13赵岽
赵 岽
(太原重工股份有限公司矫直机研究所, 山西 太原 030024)
矫直辊具有辊径与辊身长度之比很小的特点,造成矫直辊的强度与刚度都很低,因此在矫直辊上设置了多排支承辊以增加强度和刚度。宽厚板矫直辊承受矫直力大,支承辊在过大的支反力作用下会造成辊面裂纹与表面剥落的发生。
以下以1 台9 辊宽厚板矫直机为例,计算各排支承辊受力,按最大支反力分析支承辊强度。
1 宽厚板矫直机辊系的主要技术参数
1.1 支承辊
支承辊参数见表1。

表1 支承辊参数
1.2 矫直辊
矫直辊身半径为110 mm;矫直辊身长度L2为3600 mm。
2 计算各排支承辊支反力
各排支承辊布置与所受的支反力见图1 所示。
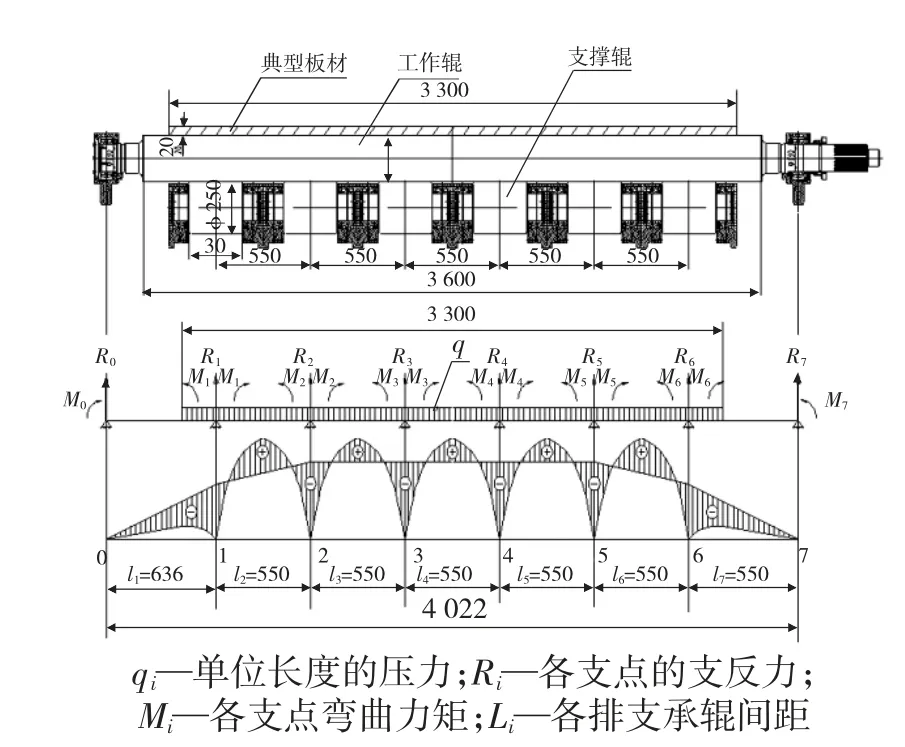
图1 支承辊布置与受力(mm)
由图1 可以看出,在得出整个矫直辊上各支点的弯曲力矩Mi后,就可进一步求出各支点的支反力Ri;各支点的支反力Ri可通过分段求出各段的支反力,再将相同支点的支反力相加得出。如:支反力R1由0~1 段的支反力R1'和1~2 段的支反力R1"组成。
通过计算已知各支点的弯曲力矩:M1=M6=-0.5×108N·mm,M2=M5=-0.65×108N·mm,M3=M4=-0.61×108N·mm,M7=M0=0[1]
2.1 计算支点0 的支反力R1

2.2 计算支点1 的支反力R0
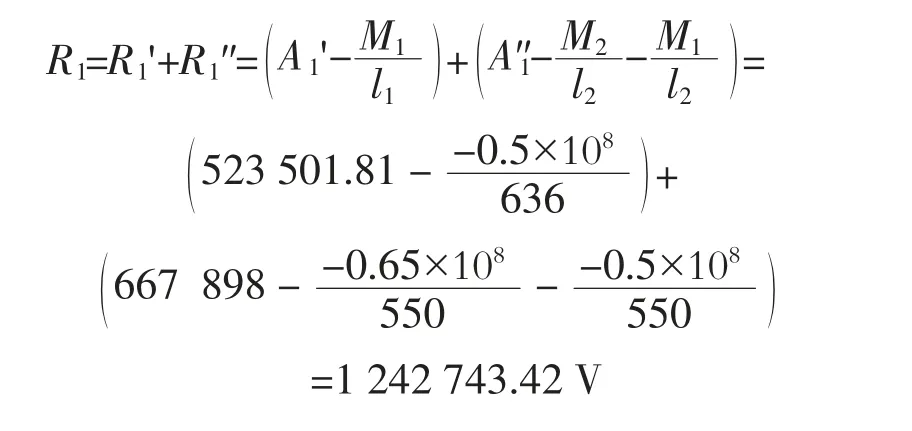
式中:A1'、A1" 为只考虑由该段外载荷对支点1 产生的支反力,N;A1'=q·l1'-A0=2428.72×275-144396.19=N;q=2428.72 N/mm[1];l1=275 mm[1]。
2.3 计算支点2、3 的支反力R2、R3

由图1 可以看出,1-2 排、2-3 排、3-4 排的作用载荷相同,故A2'+A2"=A3'+A3"=A1'=667898 N。

由于R7=R0,R6=R1,R5=R2,R4=R3,故求出R1、R2、R3后,可得出整个矫直辊上各支点的支反力,其中R2为最大支反力。
3 支承辊强度校核
支承辊垂直布置于矫直辊上,辊间接触区主要应力分布见图2 所示;由于支承辊采用简支式结构,除应对辊间接触区应力进行校核外,也需对两轴颈所受剪切应力进行校核。
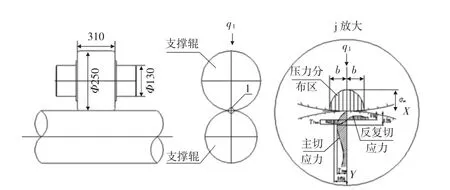
图2 支承辊与矫直辊接触区主要应力分布(mm)

式中:E 为钢质弹性模量,2.1×105N/mm2;q1为支承辊与矫直辊接触表面单位长度上的负荷,N/mm。
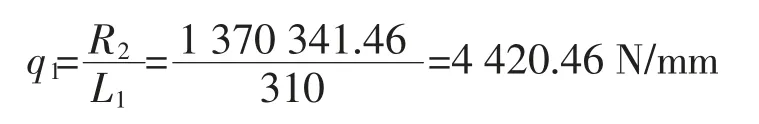
3.1 校核辊间接触区应力
在辊间接触区需按最大支反力R2校核最大压应力σmax、辊体内最大切应力τ1max、最大反复切应力τ2max。
3.1.1 计算最大压应力σmax
支承辊受弯矩产生的支反力沿轴向均布作用在辊面上,辊间接触区内产生局部的弹性压扁,材料变形处于三向压缩状态,形成半椭圆形分布的压应力,沿法向压应力最大。
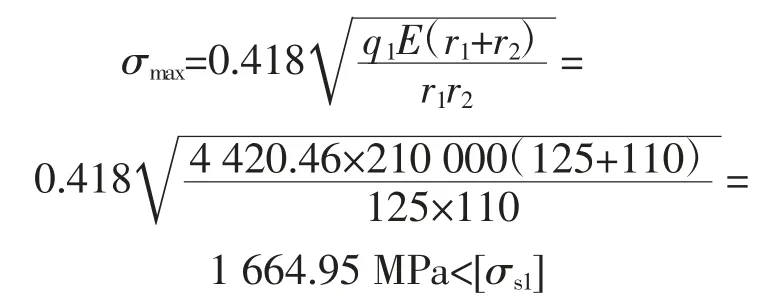
3.1.2 计算辊体内最大切应力τ1max
辊体内最大切应力在接触点处其值为零,沿着Y 方向逐渐增大,在距接触表面Y=0.78b 处达到最大切应力τ1max。
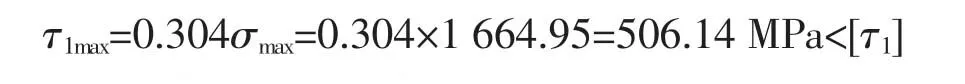
3.1.3 计算最大反复切应力τ2max
最大反复切应力τ2max沿着X 方向反复交变存在,也是造成辊面剥落的原因,在距接触表面Y=0.56,X=±0.856b 处达到最大反复切应力τ2max。
τ2max=0.256σmax=0.256×1664.95=426.23 MPa≤[τ1]
3.2 计算轴颈剪应力
支承辊两轴颈受剪,剪力之和等于支反力。

支承辊强度满足使用要求。
4 结论
以上各项分析得出,虽然辊间接触区中法向压应力最大,但材料变形处于三向压缩状态,故能承受较高的压应力,不致造成影响;而切应力的影响更容易造成辊面的开裂和辊面剥落;轴颈剪应力虽然较小,但轴颈相对辊径差值很大,截面突变很容易在轴颈根部形成应力集中,因此需要设计相应的过渡区防止应力集中而造成断裂。
宽厚板矫直机矫直辊受力大,通过增加支承辊的数量可提升矫直辊的刚度和承载能力,但在有限的矫直辊身长度上,过多增加支承辊的数量也必然会相应的减少支承辊身长度,造成接触应力增加,在设计中需兼顾两者的平衡关系。
