基于雨课堂的随机信号分析理论实践
2020-11-13徐文俊
汪 飞 徐文俊
(南京航空航天大学 江苏·南京 211106)
0 引言
随机信号分析是大学本科电子信息类必修的专业基础课,以随机过程作为学习与研究对象,概率与数理统计中随机变量的基础知识是其先导课程。当忽略随机过程的观测时间时,随机过程的取值就转变为概率论与数理统计课程中讨论的随机变量。比如古典概率中的掷色子,人们关注的是每次抛掷出现的点数,并不会去关注它出现的点数与时间的关系。随机过程具有非常明确的时间概念,它是随着时间而变化的,更贴近人们实际中遇到的生活与工程经历。[1][2]简而言之,随机过程是结合了观测时间的随机变量。随机信号分析的核心基础是充分理解概率论中的随机变量,以及随机过程等基本概念。
“雨课堂”由清华大学在线教育办公室组织研发,是一种快捷免费的为所有教学过程提供数据化、智能化信息支持的教学工具。它全面提升了课堂教学体验,具有互动性强、操作简单、反馈及时等优点。基于“雨课堂”的互联网+教学模式能够将课外预习与课堂教学相结合,让课堂互动永不下线;能够定制符合自己教学风格和教学节奏的教学设计,师生沟通及时反馈;能够实现实时答题、弹幕互动,为课堂教学师生互动提供了完美解决方案;能够科学地覆盖课堂的每一个教学环节,为师生提供完整立体的数据支持,个性化报表、自动任务提醒,使教师及时了解学生的认知水平及不懂的难点。[3]
随机信号分析教学过程中引入“雨课堂”,一方面可以利用“雨课堂”提供的各种便利新颖的教学模式,提高教学效率;另一方面可以通过有意设计课堂练习,利用“雨课堂”提供的数据报表实时将随机信号分析理论与实践相统一,达到学以致用的教学效果。
1 基于雨课堂教学数据的概率论理论实践
概率论中的随机变量是随机信号分析教学的核心基础之一。高斯型的概率密度函数是大学本科电子信息类专业最常见的一种随机变量,其数学模型表示为:
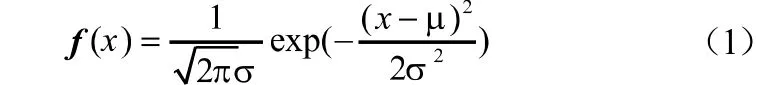
其中,代表样本值,代表均值,代表标准差。随机变量广泛采用高斯型概率密度函数是它不仅能够较好地描述绝大多数随机变量的分布特征,而且具有非常好的可微可积特性,便于数学分析计算。
为了让同学们能够更直观地理解高斯型“较好”描述随机变量的程度,可以利用“雨课堂”以身高为变量设计单项选择题。设计A 选项代表身高155~159 厘米,B 选项代表身高160~164 厘米,以此类推,任意两个选项之间的身高数据完全不重合。同学们完成单项选择之后的结果如图1(a)所示,图1(b)是用高斯型函数去拟合身高的概率统计结果。通过图1(b)的对比,可以让同学们清晰地了解到理论上的高斯型概率密度函数与现实统计数据之间的关系,认识到随机信号分析理论中常用概率密度函数的出现并不是对现实世界的准确描述,而是在近似描述现实物理现象的同时方便利用数学工具。

图1 身高的概率统计值及其高斯型拟合曲线
2 基于雨课堂教学数据的随机过程理论实践
准确理解随机过程概念是随机信号分析教学的另一个关键。简单的随机过程可以用数学模型表示为, ,其中 代表随机变量, 指观测时间起点用0 时刻表示,观测时长为。
以某一班级作为随机过程中的随机变量样本,该班对8 次课程的知识点掌握的人数统计结果如图2 所示。可以看到绝大多数同学都掌握了8 个课程的知识点,表明该班级对随机信号分析课程的学习理解能力具有平稳随机过程的特性。
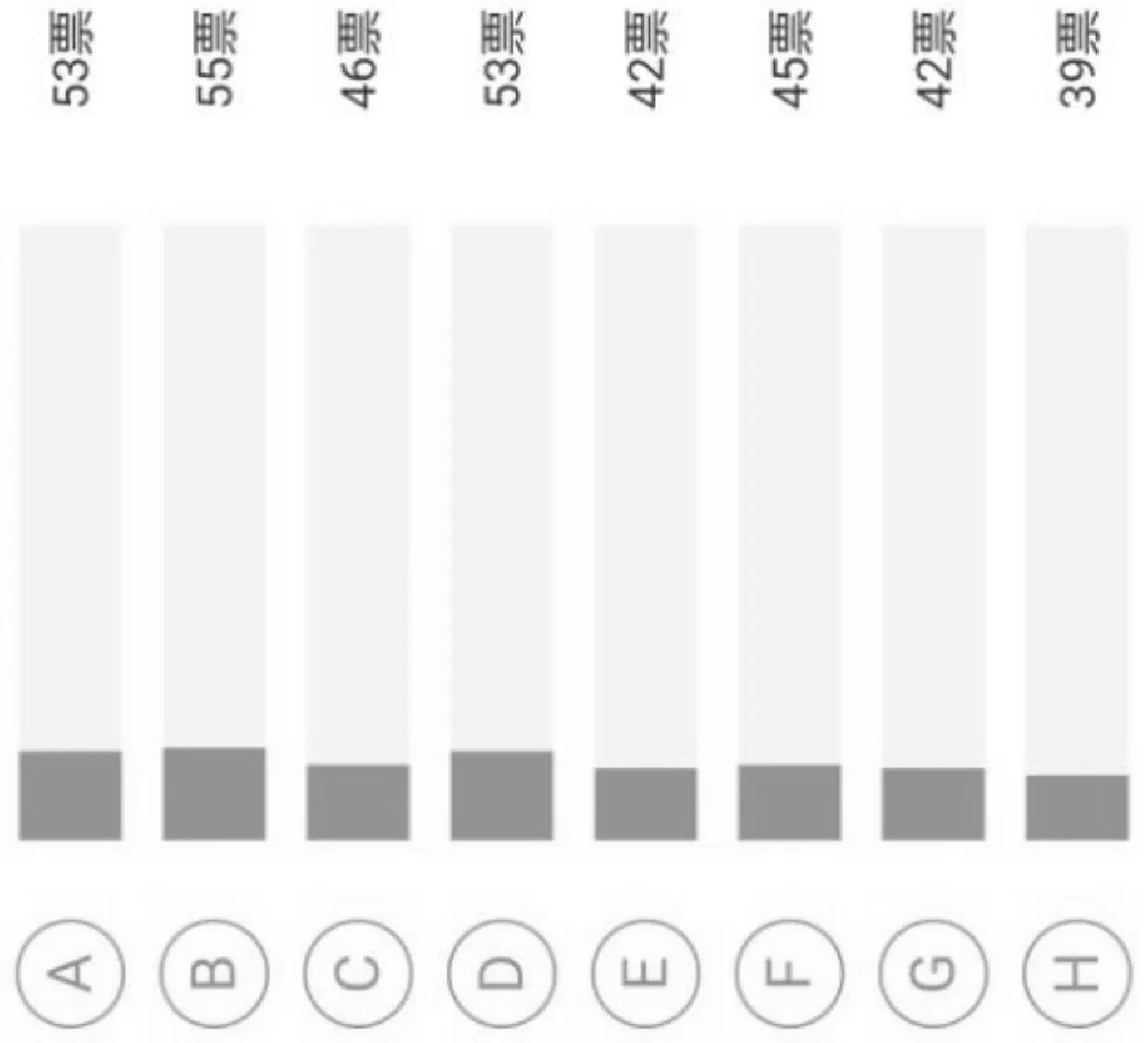
图2 以某一班级作为随机变量样本的随机过程样本
3 总结
利用随机过程分析随机信号,是在人类尚未完全掌握信号产生机制条件下趋向可知方向发展的方法,其目标是掌握随机信号的产生机制,实现可知论。随机过程是经验与知识的完美结合,充分利用“雨课堂”的特点,不仅能够实时掌握同学们的知识点掌握程度,同时能够让同学们直接将理论应用于实践。
