基于ARIMA的往复式压缩机气缸振动故障预测
2020-11-12刘喜梅曲鹏程
刘喜梅,曲鹏程
(青岛科技大学自动化与电子工程学院,山东 青岛 266100)
0 引言
故障预测历来是设备安全保障中重要的一环。近年来,各种故障预测方法层出不穷,大致可归为两大类。一类是基于设备参数的在线监测,凭借专家系统经验或技术人员现场维护实现故障类型的诊断预警。另一类则是通过数据驱动预测,应用大数据技术对故障进行预警。
在设备参数监测方面,国内石化行业有着成熟的实践经验。如:①实时监测外输泵机组的油温、转速以及振动等参数,从而有效地对故障进行诊断[1];②利用振动趋势、频谱图、时域波形图等分析手段,对参数进行实时监测,进而实现故障诊断预警[2];③采用Internet传输形式,通过分析常用内燃机监测技术,最终实现内燃机的性能监测、故障诊断和油液在线分析[3]等。
在数据驱动预测方面,高帆等应用机器学习算法对设备运行大数据进行数据挖掘,建立专家知识库,获得与故障有关的诊断规则,实现了设备故障在线预警[4]。另外,模糊C均值聚类分析算法[5]、长短期记忆(long short-term memory,LSTM)网络[6]、支持向量机(support vector machine,SVM)[7]以及整合移动平均自回归模型(auto regressive integrated moving average model,ARIMA)算法在故障预测方面都有着不错的应用效果。其中,ARIMA算法在时间序列数据预测上有着广泛的应用。
黎瑜春提出了一种基于ARIMA和反向传播(back propagation,BP)神经网络的组合预测方法[8]。该组合预测算法分别对振动序列的线性相关部分和非线性相关部分进行预测,充分利用了各单一模型的优点,提高了预测精度。李志军等则结合核主成分分析(k principal components analysis,KPCA)方法,应用ARIMA算法,以田纳西-伊斯曼(tennessee eastman,TE)过程作为研究对象,得到了较为满意的预测效果[9]。刘颖等根据汽轮机典型故障构造模拟信号,建立其ARIMA预测模型,通过聚类分析得出标准信号及待测信号的特征向量,取得了很好的预测效果[10]。周建民等运用最小二乘法估计参数建立ARIMA模型,将轴承同工况与类工况下的数据输入已建立的ARIMA模型中,对轴承故障进行预测分析,效果良好[11]。
本文选取中国石油青岛石化厂P301A往复式压缩机的气缸振动数据,通过ARIMA算法,对其机械性能故障中的振动故障进行预测预警。
1 ARIMA算法
ARIMA算法来自BOX和Jenkins的著作《时间序列分析、预测和控制》。随着其在金融、证券、航空班次、设备故障预警方面的广泛应用,逐渐形成了一整套时间序列识别、估计、建模、预测及控制的理论和方法[12]。
1.1 基本介绍
ARIMA(p,d,q)算法基于时间序列数据进行预测,包括自回归(auto regressive,AR)模型、移动平均(moving average,MA)模型、自回归移动平均(auto regressive moving average,ARMA)模型、差分(integrated,I)运算。该算法的目的是将时间序列变为平稳序列。在获取到设备的振动数据后,对数据依次进行数据预处理、时间序列平稳,然后通过自相关函数(auto correlation function,ACF)与偏自相关函数(partial auto correlation function,PACF)寻找p、q最优值,建立模型、检验模型、模型预测。
ACF用来衡量yt与yt-k之间的相关性;PACF是在去除yt-1,yt-2,...,yt-k+1之后,衡量yt与yt-k之间的相关性。
1.2 模型结构
ARIMA(p,d,q)模型包括序列的平稳性处理与ARMA(p,q)模型预测。
①平稳性处理。
ARIMA算法要求所预测的时间序列必须是平稳序列。所谓平稳,就是要求经过样本时间序列得到的拟合曲线,在未来的一段时间内仍能按照现有的形态“惯性”延续。在数学表达上,就是其均值和方差不发生明显的变化。如果不平稳,则必须进行差分处理,使之变为平稳序列。具体处理过程如下。
Δxt=xt-xt-1=xt-Lxt=(1-L)xt
(1)
Δ2xt=Δxt-Δxt-1=(1-L)xt-(1-L)xt-1=(1-L)2xt
(2)
Δdxt=(1-L)dxt
(3)
式中:xt为t时刻数据;xt-1为t-1时刻数据;L为常数滞后算子;d为差分次数。
令wt=(1-L)dxt,此时,wt变为平稳序列。将变换后的时间序列wt代入ARMA模型中,即可进行预测。由于预测序列为差分变换后的序列,因此,在预测结束后要进行预测值还原。
②ARMA模型。
ARMA(p,q)模型可表述为:
(4)
式中:γi为自相关系数;θi为移动平均系数;p为自回归阶数;q为移动平均阶数;wt为当前值;μ为常数值;{εt}为白噪声,即误差值。
当q=0时,ARMA模型变为AR(p)模型。此时,模型表述为:
wt=γ1wt-1+…+γpwt-p+εt
(5)
当p=0时,ARMA 模型变为MA(q)模型,此时,模型表述为:
wt=-θ1εt-1-…-θqεt-q+εt
(6)
1.3 模型建立及预测
①时间序列可视化,进行平稳性处理和白噪声检验。
将时间序列以时间为横轴,以预测数据为纵轴,绘制出拟合曲线,通过单位根检验法(augmented dickey fuller,ADF)判定序列平稳性。ADF的原假设是存在单位根,也即序列不平稳。只要Test Statistic统计值小于1%水平下的统计值,即可以极显著地拒绝原假设,从而认为时间序列平稳。如果ADF检验值介于1%水平下的统计值与5%、10%水平下的统计值,并不能说明时间序列不平稳,需根据具体预测的序列属性进行判断,是否需要对序列进行差分处理。若ADF检验值大于10%水平下的统计值,则必须对序列进行差分处理,再将差分后的时间序列进行ADF检验。以此方法依次进行其他步骤,直到所处理的时间序列通过平稳性检验,所进行差分处理的次数即为d值。
白噪声检验是时间序列预处理过程中非常重要的步骤,它决定了经平稳性处理后的时间序列能否进行实际预测。白噪声时间序列数据,即一组随机数据,这种数据没有研究意义。因此,一旦经平稳处理后的数据被检验为白噪声数据,就不能进行该组数据的数据预测工作。
对平稳性处理后的数据的随机性进行假设检验。其中,原假设H0是自相关系数ρ1=ρ2=...=ρk=0,而备择假设H1至少有一个自相关系数ρi≠0。在默认情况下,返回一个p值。如果该值小于10-4,则拒绝原假设,说明数据不是白噪声序列,即可进行后续预测工作。
②确定p,q的值。
画出平稳后的时间序列的ACF图与PACF图,选择合适的自相关阶数p值与移动平均阶数q值组合,然后对模型进行拟合,确定最佳p、q值组合。如果自相关系数呈指数形式衰减到0,则存在自回归过程;如果偏自相关系数呈指数形式衰减到0,则存在移动平均过程。如果上述两种情况都存在,则该序列符合自回归移动平均模型。p,q值确定规则如表1所示。

表1 p,q值确定规则Tab.1 p,q value determination rules
通过观察ACF图与PACF图,如果有多个p、q值符合要求,接下来依据贝叶斯信息准则(bayesian information criterion,BIC),从中选出最合适的参数组合。
③验证预测。
在确定好最佳p、d、q值组合后,将数据分为训练组与对照组。训练组用于训练改进模型,对照组用来对数据进行准确率验证。
④预测效果评定。
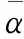
(7)
(8)

2 ARIMA算法的数据预测应用
整理往复式压缩机气缸振动数据,对其进行ARIMA时间序列预测算法建模。首先,对数据的日期进行标准化修正,对数据进行预处理。
2.1 数据预处理
所获取的数据为2015年1月4日至2018年5月3日的812个数据,往复式压缩机气缸振动数据并非每日采集,在日期上不能呈现连续性。因此,在进行预测前应进行插值,得到1 182个在时间上连续的数据。石化设备的振动速度值在短期内不会有太大的波动,一般邻近日期的值不会相差太大。本文采用线性插值的方式,对数据进行插值填充。线性插值具有简单、方便的特点,也符合石化设备运行过程的物理特性。表2为部分原始数据,表3为部分经过差值处理后的数据。

表2 部分原始数据Tab.2 Partial raw data

表3 部分处理后数据Tab.3 Partial processed data
由表3可以看出,经过插值处理后的数据在时间上实现了日期的连续性。
接下来对数据进行可视化及平稳性处理。根据1~4 h数据包含设备开机后的四组振动数据,选取设备趋于稳定后的第4 h的振动数据。数据可视化图如图1所示。
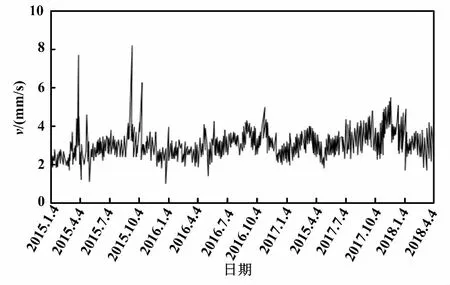
图1 数据可视化图Fig.1 Data visualization
2.2 平稳性与白噪声检验
首先,对序列进行移动平均、标准差求解,使用单位根检验法对数据进行平稳性判断,所得统计值结果为-7.434 663e×10-13,1%显著水平下的统计值为-3.436 353e×10-13。由于统计值结果小于1%显著水平下的统计值,因此可以极显著拒绝原假设,该时间序列平稳。由此可知,原始时间序列数据无需进行差分处理,d值为0。
接着,进行白噪声检验。将数据进行白噪声假设检验处理,检验结果远小于10-4,因此拒绝原假设,认为数列为非白噪声序列,可以进行后续预测工作。
2.3 确定p,q值
ACF图和PACF图如图2、图3所示。
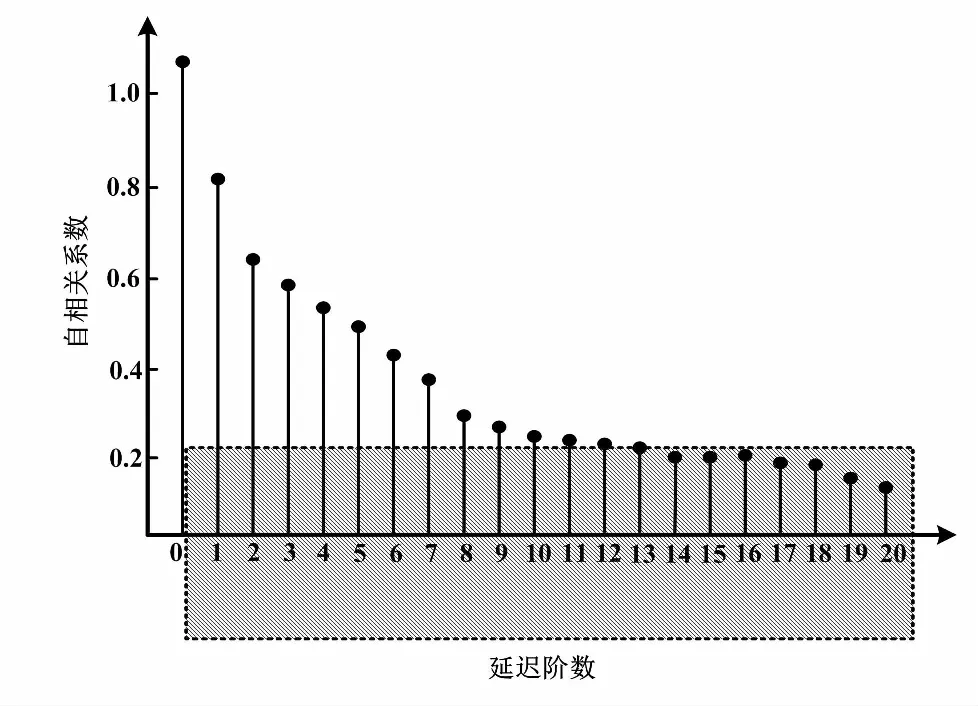
图2 ACF图Fig.2 ACF graph

图3 PACF图Fig.3 PACF graph
图2、图3中阴影部分为置信区间。从PACF图可以看到,AR(p)模型在5阶后自相关值均落于置信区间内,即p=5后偏自相关值均落于置信区间内;MA(q)模型在15阶后均有截尾现象出现。结合积分次数d=0,故预测模型的(p,d,q)=(5,0,15)。
2.4 模型预测
将插值填充后的1 182个数据分成三部分:前1 095个数据作为训练组,训练组之后的30个数据为预测组;剩余数据不作处理。
经试验数据分析,在本设备的振动故障预测上,基于ARIMA的时间序列算法有着不错的效果,且所需信息量少,运行方便快捷,结合往复式压缩机气缸振动速度安全阈值,可以为现场技术人员提供更为精准的故障预警。
预测结果与实际数据对比图如图4所示。

图4 预测结果与实际数据对比图Fig.4 Comparison between predicted results and actual data
3 结论
往复式压缩机气缸的振动频率在故障诊断中是一个重要的指标。由于其数据呈现出时间序列的特性,因此本文使用ARIMA时间预测算法对其数据进行预测,进而对故障进行预警。
通过算法实际运行,取得了较为满意的预测效果。结合其他参数的动态显示(如温度、压强等),可以为现场技术人员提供较为准确的故障预警建议,基本可以取代传统的人工巡检,减少设备因突发故障而产生的损失。
随着大数据科学的不断发展,基于数据驱动的设备故障预测与诊断将会有越来越广泛的应用。
