EFP 垂直侵彻靶板后效破片云形状描述

2020-11-12黄炫宁李伟兵郭腾飞李文彬王晓鸣

含能材料 2020年11期

黄炫宁，李伟兵，郭腾飞，李文彬，王晓鸣

（1. 南京理工大学智能弹药技术国防重点学科实验室，江苏南京 210094；2. 西安现代控制技术研究所，陕西西安 710065）

1 引言

爆炸成型弹丸（Explosively Formed Projectile，EFP）战斗部对装甲目标毁伤效能的评估取决于EFP 的侵彻深度和靶板后效破片对装甲目标内部仪器、仪表及有生力量的打击能力。随着数值模拟研究手段的日趋成熟，国内外学者对EFP 毁伤元的成型、稳定飞行以及侵彻的研究取得了长足的进步，积累了大量研究数据［1-3］。但针对EFP 侵彻有限厚靶板的后效研究相对较少，未能全面、准确地评估EFP 对装甲目标的毁伤效能，因此EFP 的靶后效应研究以及EFP 对装甲目标毁伤效能评估应是下一步研究工作的重点。

Arnold W［4］提出聚能射流（JET）的靶后破片云为空心椭球。相较于JET，EFP 弹径较粗，侵彻孔径较大，穿透靶板后在装甲目标内部会形成毁伤面积相对较大的破片场。Carleone J［5］基于X 光试验结果，对比分析了JET 和EFP 的侵彻后效，结果表明，EFP 靶后破片的密集度及数量大于JET，因此，针对EFP 靶后效应的研究逐步展开。Kim H S［6］等在不考虑质量大、速度低的环状破片的情况下，建立了靶板后效破片云椭圆参数方程，得到了靶后破片的散布特性、最大径向飞散速度。针对靶后效应仿真方法的研究，Dalzell M W［7］等采用AUTODYN 软件中的SPH 算法对EFP 侵彻靶板后效破片进行仿真研究，认为SPH 算法对靶后破片的模拟优于Lagrange、Euler 算法。国内学者对靶后破片的研究多基于动能杆式弹［8-9］，对EFP 后效的研究则相对较少，主要基于工程试验、侵彻理论对EFP 靶后破片的数量、质量等分布特性进行研究。张先锋［10］通过建立的EFP 侵彻有限厚靶板模型，计算得到了侵彻体剩余长度、剩余速度等后效参数。王昕［11-12］等通过试验研究了不同靶板厚度对EFP 靶后破片数量散布及侵彻能力的影响，且采用FEM⁃SPH 自适应转换算法，得到了靶后破片数量、速度空间分布的工程计算模型。邢柏阳［13-14］考虑EFP 变截面的特性，改进了EFP 靶后破片质量模型，并得到了平均应变率和Mott 公式的拟合因子，从而获得了靶后破片数量和质量分布的计算方法。而关于EFP 后效破片云形状的研究中，叶严［15］在一定的假设基础上，从崩落环的飞散特性出发，建立了EFP 垂直侵彻靶后破片云形状描述模型，破片云长半轴、短半轴均为靶板背面最大开孔孔径的单值线性函数。曹兵［16］、王昕［11-12］采用X 光摄像技术获得了EFP 靶后破片云形状，计算了飞散角、长短轴之比，但是没有具体给出破片云形状参数的与弹靶参数的定量关系。

上述研究中EFP 后效破片云形状描述模型主要涉及了靶板背面最大开孔直径，并未涉及EFP 参数。而空间防护领域中超高速碰撞碎片云形状描述发展较成熟，区分了弹丸碎片云、薄板碎片云和中心大碎块［17］，且涉及多层薄板的各层碎片云形状［18］。

因此，为了准确描述EFP 垂直侵彻有限厚靶板后效破片云的形状，本研究基于量纲分析和正交设计理论，结合数值模拟的研究手段建立了破片云形状参量与EFP 成型参量、弹靶材料参量的关系，并将计算结果与仿真结果及相关试验结果进行了对比，以期为破片云对靶后目标的毁伤效能评估工作提供参考。

2 破片云形状分析及基本假设

EFP 对有限厚靶板的侵彻过程可分为塑性侵彻阶段、剪切带或拉伸断面的形成阶段、冲塞穿透或崩落飞出阶段［10］。当剪切带或崩落拉伸断面完全形成后，剩余EFP 从靶体冲出，其后跟随着弹、靶材料的碎片以及靶板背面的崩落环，将这些具有杀伤力的破片称为靶后破片。靶后破片在飞散过程中经碰撞、冲击波冲击等作用，形成某一稳定状态等比例地向外膨胀，将达到稳定状态瞬时的靶后破片云称为初始靶后破片云［19］。

典型的破片云形状如图1 所示：破片云整体呈椭球形，最前端为剩余EFP，中间部分为EFP 和靶板材料的碎片，最末端是由冲击波运动至靶板背部自由界面（空气阻抗远小于靶板阻抗，可近似为自由界面）反射形成的拉伸波导致靶背崩落生成的崩落环。当崩落拉伸断面完全形成后，剩余EFP、弹靶材料碎片、靶板崩落物经P（靶板背面与弹轴线的交点）点喷发，向外飞散。由于崩落环质量大、速度低［4，6］，且其空间分布不符合大部分破片的分布规律（整体呈椭球形），不予考虑，据此可以认为破片云最前端至靶板背面的距离为破片云长轴长2a，破片云中垂直弹轴方向最大截面直径为短轴长2b。

考虑靶后破片的形成及飞散过程极其复杂，从鼓包破裂到靶后破片云形成之间的时间间隔非常短［19］，且稳定后的破片云长轴随时间近似呈线性增大［20-21］，为了对问题进行简化，在后续研究中进行如下假设：

（1）破片云形态可以描述为一个空心椭球［4，6］；

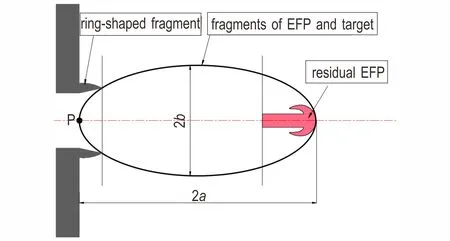
图1 破片云形状示意图Fig.1 Diagrammatic sketch of the debris cloud shape

（2）当崩落拉伸断面完全形成后，认为靶后破片直接进入初始靶后破片云阶段，即以稳定状态等比膨胀；

（3）破片云中所有破片均由P（见图1）点喷发，且沿初始飞散方向作匀速直线运动。

3 基本模型

3.1 破片云形态影响因素分析

依据假设（1），靶后破片云的形态可以通过一个简单的椭球方程进行描述。考虑到对称性，可以简化为一个椭圆方程。故在图1 的基础上建立以下坐标系：以P 点为原点，以EFP 飞行方向为x 轴正向，以向上飞散的破片径向飞散速度方向为y 轴正向。那么，初始靶后破片云的形状就可以描述为：

根据方程（1），只要确定长半轴a 及短半轴b 的值，就可以确定椭圆方程。再由假设（2），破片群体进入初始靶后破片云阶段后，椭圆长半轴与短半轴的比值就成为了一个相对固定的值，将该比值定义为E（即E=a/b），取E=1.5［21］。式（1）可转化为

对于式（2），得到参量a 就可以对初始靶后破片云的形状进行数学描述。故应当建立破片云长半轴a 与EFP、靶板参数的关系。

在侵彻行为中，影响侵彻效率最关键的因素为弹靶材料密度比。故影响破片云形态的主要因素为EFP的成型参数（实心长度l、最大实心直径d、着靶速度v），靶板厚度t、弹靶材料参数（药型罩密度ρp、靶板密度ρt、靶板屈服极限Y 以及靶板杨氏模量Et）。所涉及的弹靶参数如图2 所示。

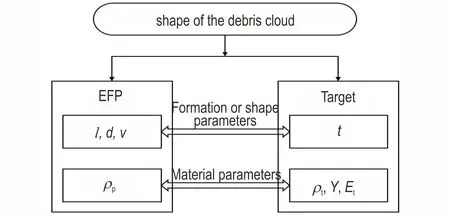
图2 破片云形态的影响因素Fig.2 Influencing factors of the debris cloud shape

3.2 长半轴a 的量纲分析

模型试验是解决物理模型尚不清楚的问题的有效办法，通过模型试验或数值模拟的方法得到

式中，n 为该物理模型所涉及的所有物理量的个数，k为独立量纲参量的最大数目。只要使得模型中的Π1，Π2，……Πn-k与原型分别对应相等，该物理问题便相似。层裂不服从几何相似率［22］，并且引起的靶后破片主要为质量大、速度低的环状破片，在本研究中不予考虑。在剔除崩落环的情况下，研究长半轴的相似性。

根据图2 可得：

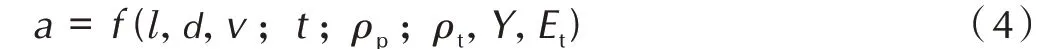
选取d、ρp、Y 为基本量，通过量纲变换可以将上式转化为几个无量纲量之间的关系，即：

式中，有三项物理参量，两项几何参量，若模型与原型速度相同、弹靶材料相同、几何相似，则模型与原型相似。

为了确定式（5）中的f，结合式中的参量对杆式弹正撞击靶后破片云长半轴的工程模型进行修正。由文献［19］可得杆式弹正撞击靶板后效破片云长半轴为：

结合式（5）对式（6）进行修正，增加式（5）中相应的无量纲量修正项，从而引入EFP 实心长度l、弹靶材料密度ρp、ρt、靶板屈服极限Y 以及靶板杨氏模量Et等参量，能够反映EFP 成型参数、弹靶材料参数对破片云形状的影响。则初始靶后破片云长半轴可以表示为：

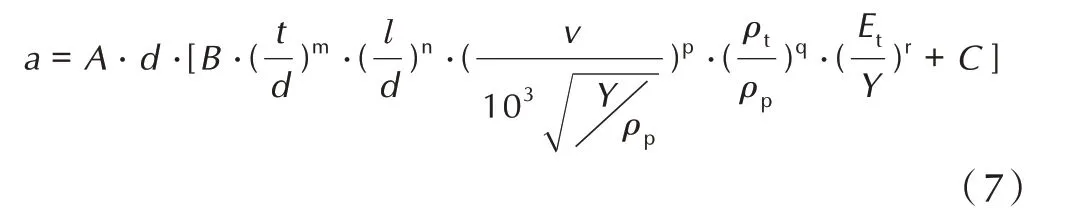
式中，A、B、C、m、n、p、q、r 为待拟合参数；d 为EFP 最大实心直径，mm；l 为EFP 实心长度，mm；t 为靶板厚度，mm；v 为EFP 着靶速度，m·s-1；ρp、ρt分别为药型罩、靶板的密度，g·cm-3；Y、Et分别为靶板屈服极限、杨氏模量，GPa；a 为初始靶后破片云长半轴，mm。只要确定出待拟合参数的具体数值，就可以建立长半轴a 与EFP、靶板参数的关系，进而可以对初始靶后破片云形状进行准确描述。

4 初始靶后破片云形状描述与验证

4.1 EFP 等效模型的建立

通过大量的数值模拟对式（7）进行参数拟合，就需要研究EFP 的各个成型参数对初始靶后破片云形状的影响。但由于EFP 的成型受药型罩结构、装药结构、起爆点位置等诸多因素的影响，很难对单个成型参数进行规律性定量调控，而目前大多数研究［1，12，23-24］都是通过建立EFP 的等效模型来解决该问题，且解决了EFP从成型、飞行、侵彻到靶后破片飞散等一系列过程所涉及的网格畸变、计算量大的问题，提高计算精度。故有必要先建立EFP 的等效模型。

4.1.1 形状模拟

采用装药口径为Dk、装药高度为H、壳体厚度为ts的成型装药结构，如图3 所示，炸药采用JH⁃2，药型罩材料为紫铜，起爆模式为药型罩顶端单点起爆。经过数值模拟计算，EFP 的实心长度l为56.948 mm、最大实心直径d 为24.444 mm、着靶速度v 为2317 m·s-1，对45#钢靶的侵彻深度h 为77.720 mm。EFP 成型形状如图4a 所示，在此基础上建立EFP 的等效模型如图4b 所示。EFP 模拟弹与真实EFP 的具体参数如表1 所示。

图3 成型装药结构图Fig.3 The diagram of shaped charge

由图4及表1可知，EFP模拟弹与真实EFP在形状和质量上相近。由于弹丸的侵彻行为直接影响着靶后破片的特性，因此，为了进一步验证该模拟弹的等效性，将真实EFP与EFP模拟弹的侵彻效果进行对比研究。

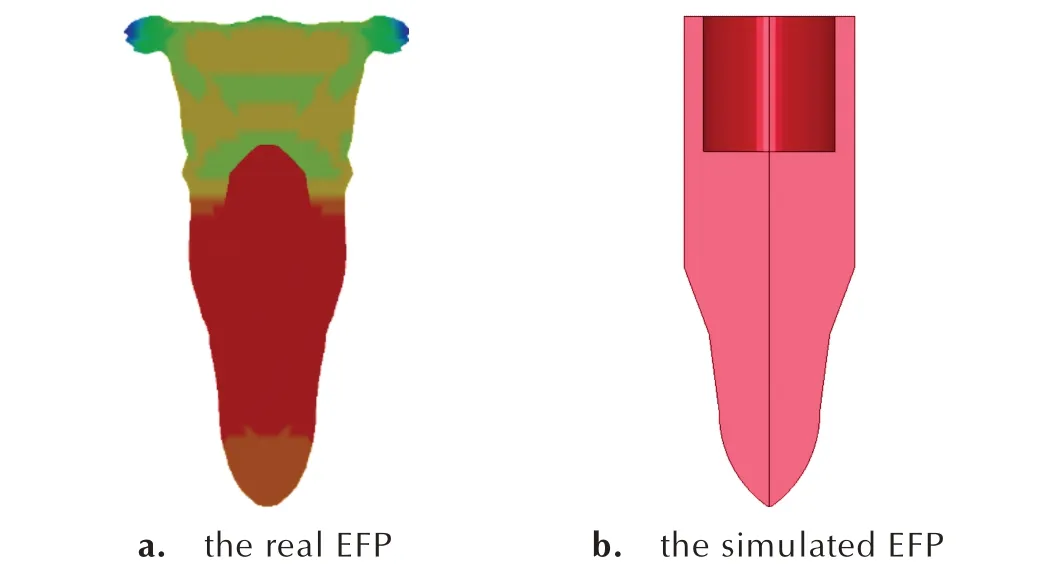
图4 EFP 形状Fig.4 The shape of EFP

表1 EFP 模拟弹和真实EFP 的参数对比Table 1 Comparison of parameters between the real EFP and the simulated EFP

4.1.2 侵彻效果验证

EFP 的侵彻性能主要为侵彻深度、侵彻孔径。其中：侵彻深度决定了弹丸对靶板的穿透能力，进而影响靶后破片云的形成与头部膨胀速度；根据文献［6，15，19，25］，入孔直径与靶板后效破片的形成及飞散过程无直接关联，因此，本研究对侵彻深度、出孔孔径进行对比验证。

考虑EFP 模拟弹的材料为紫铜，屈服极限较低，试验中利用火炮发射很难保证弹丸在满足发射强度的条件下加速到真实EFP 的速度（2317 m·s-1），为了便于研究，利用AUTODYN 仿真软件，建立EFP 模拟弹侵彻钢锭的二维轴对称仿真模型，如图5 所示，侵彻靶板直径为180 mm，厚度为100 mm。弹丸与靶板均采用Lagrange 算法，两个Part 的材料模型如表2 所示，具体材料参数见表3［26］。赋予EFP 模拟弹2317 m·s-1的初始速度，计算该模拟弹对钢锭的侵彻，得到其侵彻深度h 为78.18 mm。

表2 EFP 模拟弹和靶板的材料模型Table 2 Material model of the simulated EFP and target plate

针对图3 所示成型装药结构，进行EFP 威力侵彻试验，试验布置如图6 所示，靶块的材料及尺寸与仿真完全相同，测量侵彻深度为85 mm。

对比侵彻深度可知，真实EFP 与EFP 模拟弹对钢靶侵彻深度的仿真值基本一致，与真实EFP 试验值的误差均控制在8%左右。并计算获得靶板厚度分别为20，30，40 mm 和50 mm 时，真实EFP 与EFP 模拟弹的侵彻出孔孔径Dc，如图7 所示。分析图7 可知：真实EFP 与EFP 模拟弹的侵彻出孔孔径与靶板厚度均呈正相关，且同一靶板厚度下，两者相对误差在8%以内。

综上，可以认为该等效模型能够模拟真实EFP 的侵彻行为，证明了等效模型的可行性。

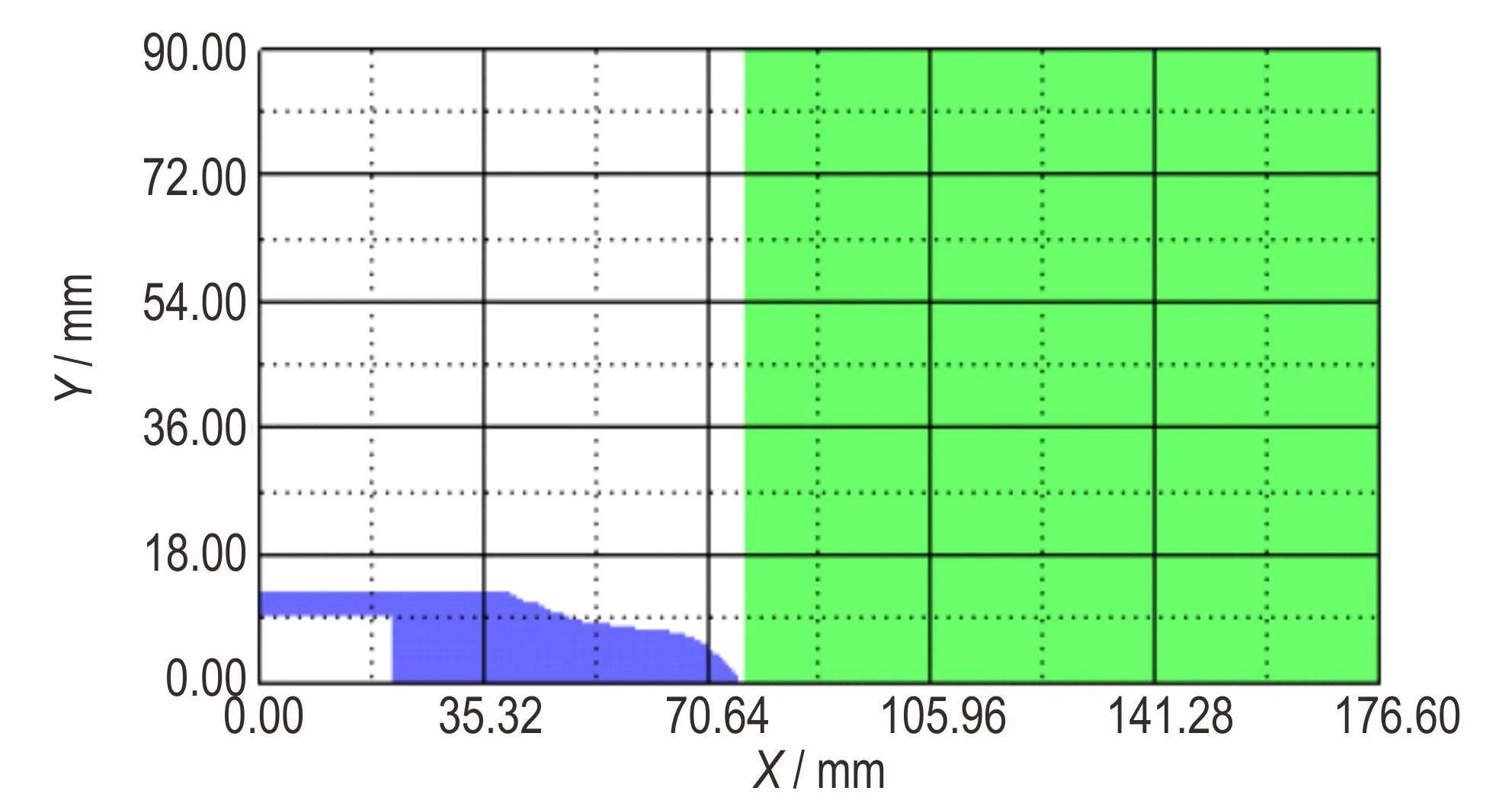
图5 EFP 模拟弹侵彻靶板仿真模型Fig.5 Simulation model of the penetration of target plate by simulated EFP

表3 EFP 模拟弹及靶板材料参数Table 3 Material parameters of the simulated EFP and target plate

图6 EFP 威力侵彻试验布置图Fig.6 Test setup diagram of EFP penetration

图7 不同靶板厚度下EFP 的侵彻出孔孔径Fig.7 Penetration exit hole calibers of EFP under different target thicknesses

4.2 椭圆方程的建立

基于EFP 的等效模型研究EFP 垂直侵彻有限厚靶板后效破片云的形状。由于Lagrange 算法侵蚀失效设置的必要，在计算连续体碎裂的过程中会导致靶后破片的形成无法有效地描述。而SPH 算法是一种无网格的Lagrange 算法，可用于解决连续体结构的碎裂、固体的层裂、脆性断裂等问题，适用于靶板贯穿过程的计算模拟［27］。因此，弹丸与靶板均采用SPH 算法，弹丸根据图4b 建立几何模型，同时建立长、宽均为200 mm 的靶板模型，然后用SPH 粒子进行填充，其中，SPH 粒子直径为0.8 mm，在靶板边界设置固定约束，并对弹丸施加初始速度，仿真模型、弹靶材料模型及参数见图5、表2 和表3。

由前文知，本研究对靶板的研究范围应限于45#钢，根据文献［10］，45#钢的屈服极限Y 为2.1 GPa、密度ρt为7.85 g·cm-3、杨氏模量Et为209.822 GPa。因此，在靶板材料参数确定的基础上研究破片云长半轴a 与EFP 实心长度l、最大实心直径d、着靶速度v、密度ρp及靶板厚度t 等参数之间的关系。

根据表1，选取EFP 实心长度l 的变化范围为38～70 mm（参量增量为8 mm）；EFP 最大实心直径d 的变化范围为22～30 mm（参量增量为2 mm）；EFP 着靶速度v 的变化范围为1500～2300 m·s-1（参量增量为200 m·s-1）；EFP密度ρp为2.71，7.85，8.96，16.65 g·cm-3和19.22 g·cm-3；靶板厚度t 的变化范围为10～50 mm（参量增量为10 mm）。

基于上述仿真方案，若进行全面研究，需要穷尽55次数值计算，仿真规模过大，耗时过长。因此，利用正交设计理论，得到表4 所示的正交设计因素水平表。针对表4 中5 因素5 水平的情况，可利用正交表L25进行计算分析。由于方案较多，不一一列举仿真结果，列出如图8 所示的方案5、10、15、25 下的初始靶后破片云图。统计E=1.5 的工况下各方案初始靶后破片云长半轴a 的值，L25及长半轴a 的计算结果见表5。其中“-”表示弹丸未穿透靶板或靶后破片极少的情况，未作统计。

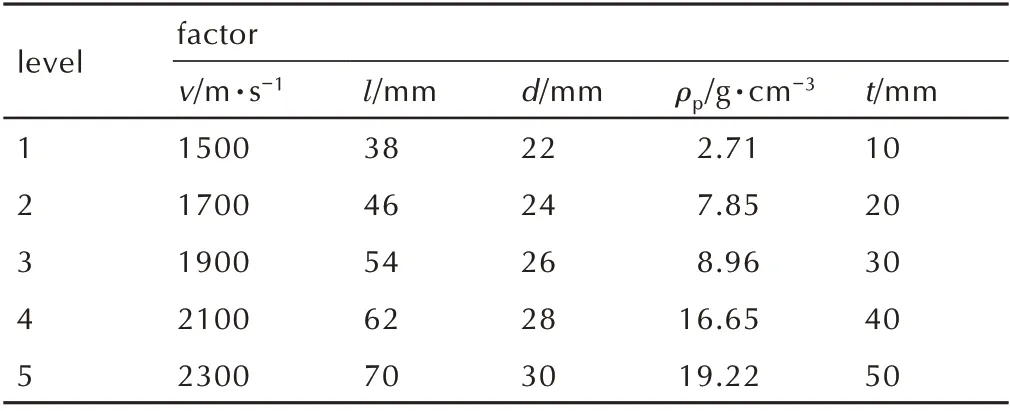
表4 正交设计因素水平表Table 4 The level factors for orthogonal design

图8 方案5、10、15、25 下破片云形貌图Fig.8 Debris cloud morphology of schemes 5，10，15 and 25

结合表5 对式（7）进行非线性函数拟合，利用Ori⁃gin 软件中自定义多自变量多参数函数功能，得到各拟合参数的值，如表6 所示。故，最终得到初始靶后破片云长半轴a 的表达式如式（8）所示，将式（8）代入式（2）即可得到EFP 垂直侵彻初始靶后破片云椭圆方程。

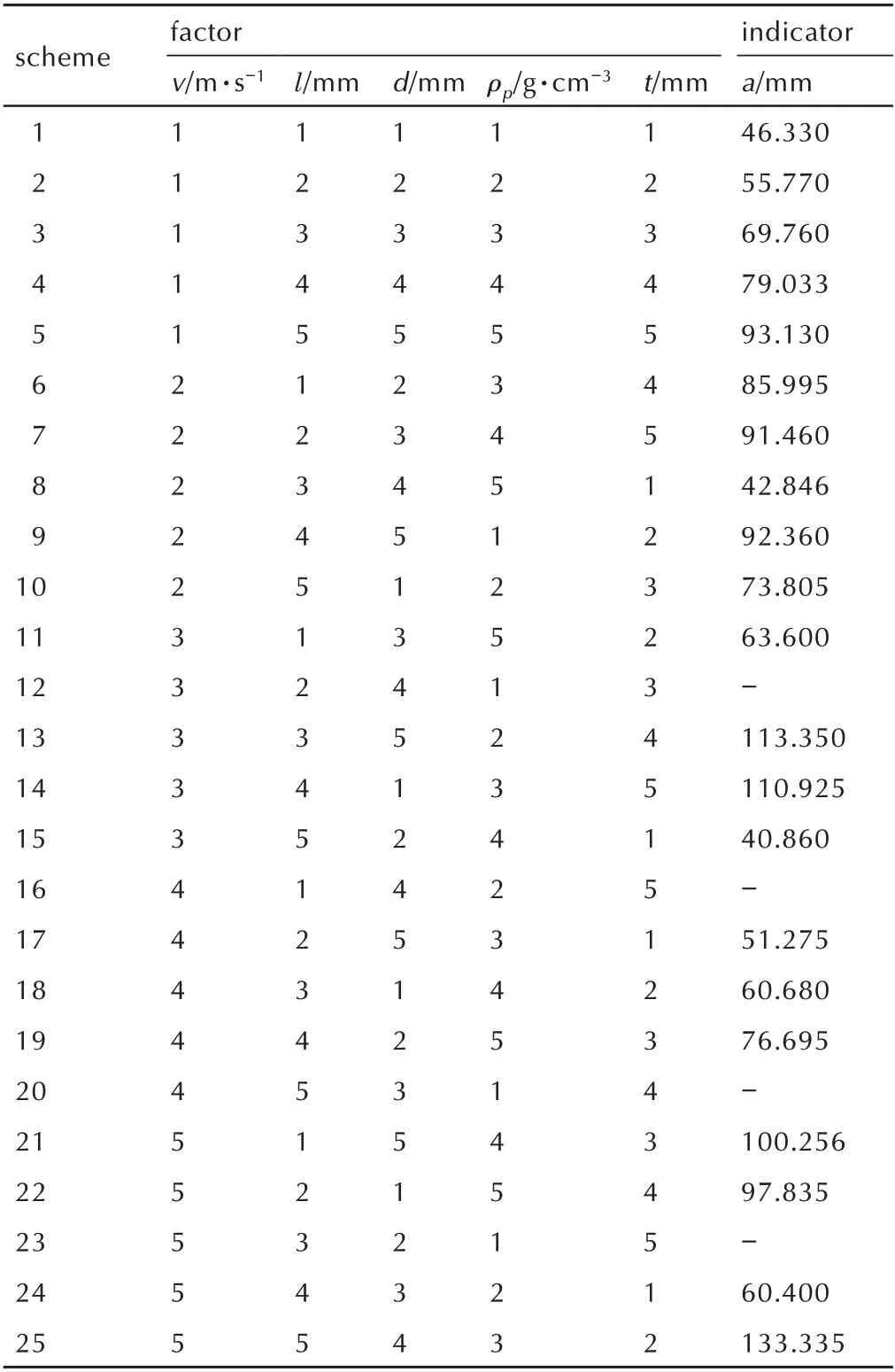
表5 破片云长半轴正交计算表Table 5 Orthogonal table of debris cloud major semi⁃axis

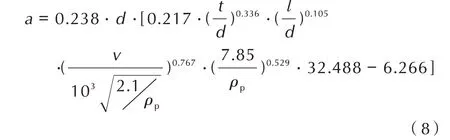
表6 破片云长半轴拟合结果Table 6 Fitting results of debris cloud major semi-axis

4.3 模型有效性验证

4.3.1 数值计算与模型计算对比

EFP 着靶速度v 直接决定了靶后破片云的轴向膨胀能力，是影响靶后破片云形态的关键因素。控制EFP 模拟弹的实心长度l 为55.45 mm、实心直径d 为26 mm、密度ρp为8.96 g·cm-3、靶板厚度t 为20 mm不变，计算EFP 着靶速度v 在1500～2300 m·s-1之间变化时，初始靶后破片云的形状参量，并与本研究所建立的破片云描述模型计算结果进行对比，得到如图9 所示的变化规律曲线及误差分布图。

分析图9a 可知：随着EFP 着靶速度v 的增加，破片云长半轴a 的计算值及仿真值均呈上升趋势，且着靶速度v 由1500 m·s-1增加至2300 m·s-1时，计算结果增加了65.08%、仿真结果增加了58.74%。这是因为EFP 着靶速度的增加导致其在遭遇并贯穿相同的靶板目标时，剩余EFP 及二次破片的飞散速度增加，破片云膨胀能力增强，故，破片云长半轴随之增大。

观察图9b 可得：EFP 着靶速度v 从1500 m·s-1增加至2300 m·s-1时，破片云长半轴a 的计算值与仿真值的相对误差均控制在11%以内，且v 为1900 m·s-1时，计算结果与仿真结果吻合最好，相对误差降至1.84%左右，表明了该破片云数学描述模型的准确性。

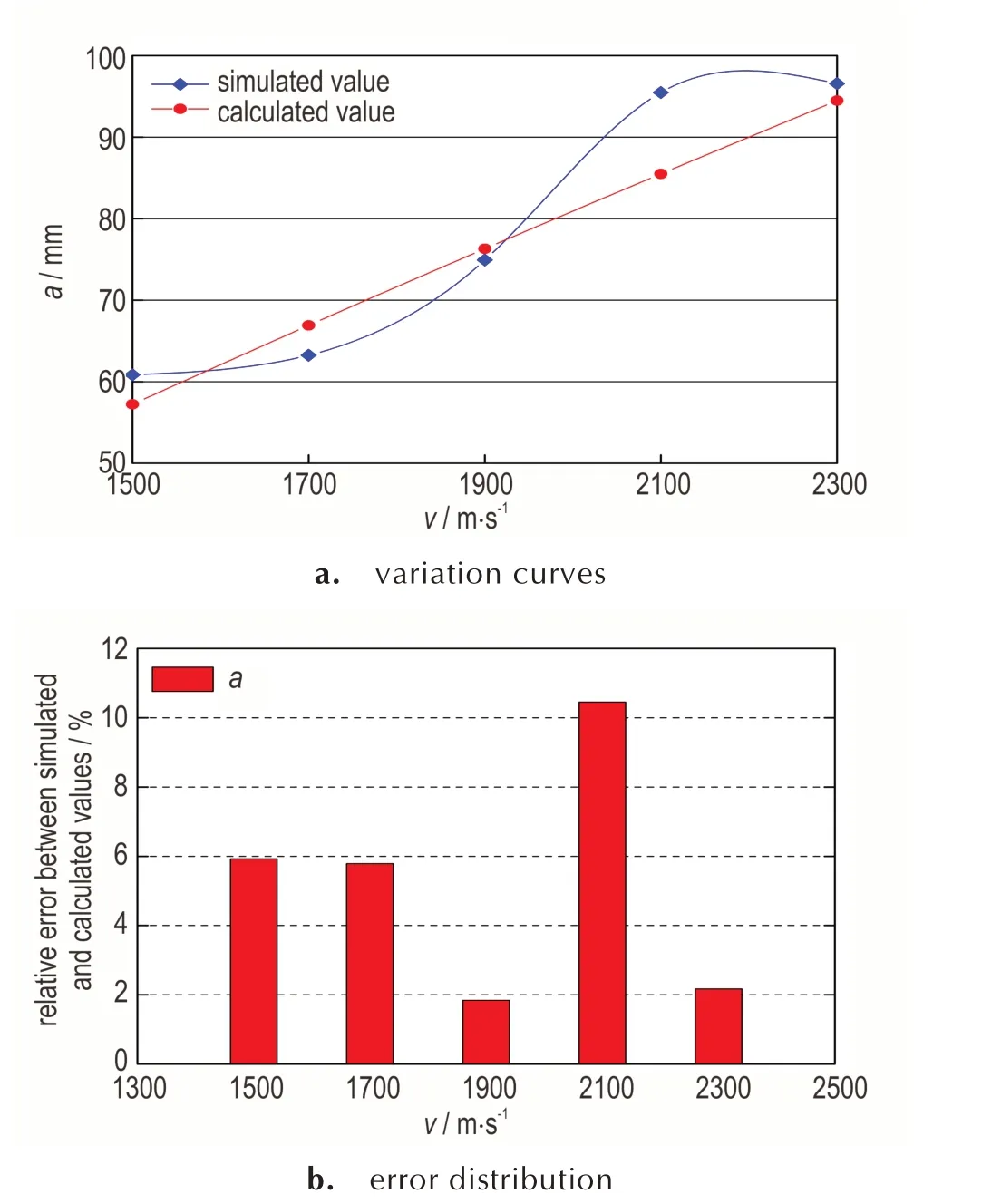
图9 不同EFP 速度下破片云长半轴a 的计算值与仿真值及其误差分布Fig.9 Calculated value，simulated value and error distribu⁃tion of debris cloud major semi⁃axis a with different EFP ve⁃locities v

4.3.2 试验验证

利用本研究所建立的破片云描述模型对文献［11］中EFP 垂直侵彻20 mm 厚45#钢靶后效破片云长半轴进行计算。根据文献［11，28］，该破片云试验所用EFP 的具体参数如表7 所示。