基于改进的FA2BOUG法研究北极美亚海盆区域的布格重力异常特征
2020-11-12赵俐红庞贝贝凌子龙马媛媛曲彦丞
赵俐红,庞贝贝,凌子龙,马媛媛,曲彦丞
(1.山东科技大学 地球科学与工程学院,山东 青岛 266590;2.青岛海洋科学与技术试点国家实验室 海洋矿产资源评价与探测技术功能实验室,山东 青岛 266237)
北冰洋以罗蒙诺索夫海岭(Lomonosov Ridge)为界,分为欧亚海盆(Eurasia Basin)和美亚海盆(Amerasia Basin)。欧亚海盆是北极地区地质年龄最小的海盆,具有明显的磁异常、重力异常特征,其构造演化历史较为清晰。与欧亚海盆不同,美亚海盆地质年龄大、面积广,并且由于缺乏可靠的地质地球物理资料,在认识其构造演化历史等方面存在很大争议[1]。美亚海盆的主要海岭、海盆(如阿尔法-门捷列夫海岭(Alpha-Mendeleev Ridge)和波德沃德尼科夫海盆(Podvodnikov Basin)的岩石圈性质、年龄和成因仍存在很大争议。
迄今为止,北极地区仍是多个国际科学研究计划的关键地区,有关该地区的研究不仅具有深远的政治意义,而且在海洋、冰川、气候、地质等领域亦具有重要的科学意义。1998年,Grantz等[2]根据重力数据推断加拿大海盆存在一个古洋中脊。2007年,俄罗斯在北极地质大断面的调查研究中,证实了门捷列夫海岭属于减薄的陆壳[3]。2012年北极潜艇科学项目(Submarine Arctic Science Program)在加科尔洋中脊(Gakkel Ridge)、罗蒙诺索夫海岭、楚科奇边缘地(Chukchi Borderland)获得了大量的多波束地形、声呐等数据,这些数据都对研究北冰洋的地质与构造演化具有重要意义[4]。
布格重力异常包含了地壳内各种偏离正常密度分布的地质构造的影响,也包括了地壳下界面起伏而在横向上相对于上地幔质量的巨大亏损(山区)或盈余(海洋)的影响,对于研究地壳结构具有重要作用。海洋布格重力异常的校正工作主要包含中间层(海水)校正以及地形校正。Parker[5]在1973年通过在位场界面正演计算中引入快速傅里叶变换,极大地缩短了计算所用的时间,消除了较早的传统方法用公式逐点进行计算而忽略临近地形影响的缺点[6]。Parker[5]法在计算重力异常时,需要使用一个平均地形值,导致其在地形变化较大的区域存在偏差。Fullea等[7]在2008年提出了FA2BOUG法,该方法逐点计算研究区的布格重力异常值,不需要使用平均地形值,在计算每一点过程中,考虑到研究区其他点对该点的重力影响,消除了忽略临近地形影响的缺点。但这一方法缺陷是在计算过程中不能很好地消除沉积物的影响[8]。为解决这一问题,本文将沉积物转化为等质量的岩石得到等效地形,利用等效地形计算布格重力异常。
1 数据来源
研究区为北极美亚海盆地区,即105°E~50°W,65°N~90°N(图1)。水深数据采用的是全球海陆地形数据库(General bathymetric chart of oceans,GEBCO)海底2030项目发布的2019年最新全球水深网格数据[9],采样间隔是15弧秒。空间重力异常数据(Free air Gravity Anomalies,FAA)使用的是世界重力模型2012(World Gravity Model 2012,WGM2012模型)[10],采样间隔为2弧分(图2)。沉积层厚度数据使用新的全球5弧分总沉积厚度网格——全球沉积物(Global Sediment,GlobeSed)[11](图3)。为减少由于曲线坐标的平面处理而产生的误差,使用极地立体投影,即将所有的数据集均投射到笛卡尔坐标系中,投影中心设定为150°W、90°N。
2 研究区概况
美亚海盆包含阿尔法-门捷列夫海岭、加拿大海盆(Canada Basin)、马卡罗夫海盆(Makarov Basin)以及波德沃德尼科夫海盆(图1)。加拿大海盆位于美亚海盆的南部,长约1 500 km,宽1 100 km,是北冰洋面积最大的海盆[12],海盆底部为平坦的加拿大深海平原,大部分海域水深在3 000~3 500 m;加拿大海盆中央有一条明显的南北向的“反S”型的空间重力负异常带[13],其重力异常值明显低于两侧。加拿大海盆北部为阿尔法-门捷列夫海岭,西部为楚科奇边缘地,东南方向与加拿大北极群岛的大陆边缘接壤,西南方向为阿拉斯加北极区域;加拿大海盆沉积厚度从楚科奇边缘地向阿拉斯加边缘增加,厚度最大处超过15 km[14]。马卡罗夫海盆和波德沃德尼科夫海盆被罗蒙诺索夫海岭和阿尔法-门捷列夫海岭所包围,波德沃德尼科夫海盆毗邻东西伯利亚边缘的水深达2 800 m,马卡罗夫海盆水深约为4 000 m[15]。阿尔法-门捷列夫海岭从西部的弗兰格尔岛起,延伸到埃尔斯米尔岛,总长约1 700 km,宽200~700 km,总面积70万km2,水深约2 000 m。
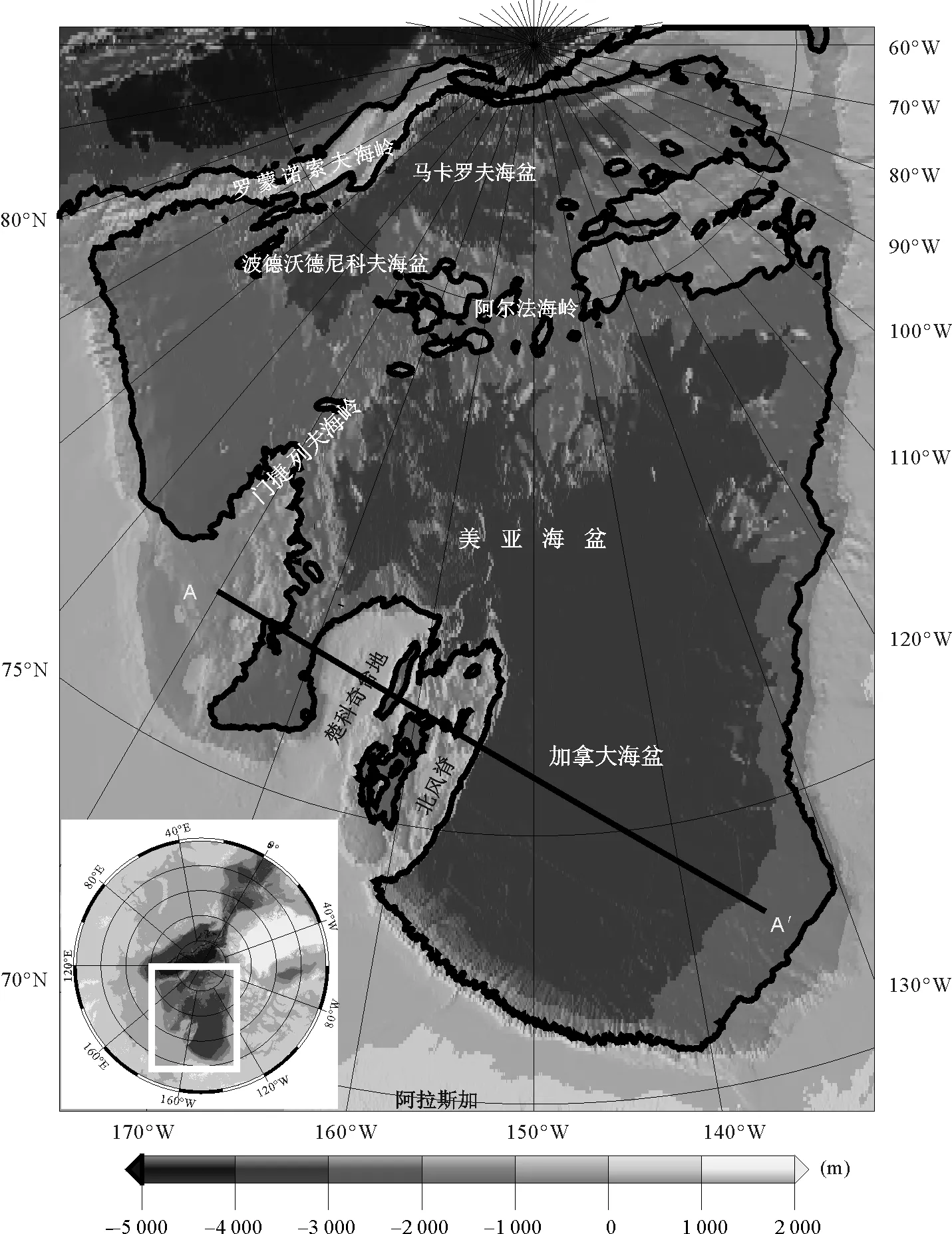
小图为北极区域地形图,白色框为研究区范围;经纬度105°E~50°W,65°N~90°N图1 美亚海盆水深图Fig.1 Bathymetric map in the Amerasia Basin
当前,由于美亚海盆的地质地球物理资料较少,且频繁的火山活动一定程度上扰乱了海盆区的磁性特征,致使其张开时间很难被确定[15]。在北冰洋张开之前,北极地区构造主体是北极克拉通,周边分别是不同时期的造山带,而美亚海盆的门捷列夫海岭、阿尔法海岭、楚科奇边缘地均为陆壳,应该是北极克拉通的一部分[12]。在中—晚侏罗世全球泛大陆裂解的背景下,加拿大海盆开始形成,但由于缺少地质地球物理资料的约束,其具体的海底扩张时间存在很大的争议,有观点认为是在140~133 Ma[16],也有观点认为大约开始于145 Ma[15]。有关加拿大海盆的构造模式归纳起来主要可以分为三类:陆壳洋壳化、古洋壳的捕获和海底扩张,目前大部分学者支持海底扩张模式,但对扩张方式又存在四种不同的解释模型,分别是:逆时针旋转模型、北极群岛走滑模式、北极阿拉斯加转换模式以及Yukon走滑模式[17],目前主流模型是Grantz提出的基于“逆时针旋转”的“挡风玻璃雨刮式”模型。而对于整个美亚海盆的成因,虽主要认为是在原地扩张而形成的,但对其扩张的方向以及位置尚存在不同观点[18]。

黑色粗线为2 000 m等深线;1—罗蒙诺索夫海岭;2—马卡罗夫海盆;3—波德沃德尼科夫海盆;4—阿尔法海岭;5—门捷列夫海岭;6—楚科奇台地;7—北风脊;8—加拿大海盆;9—阿拉斯加图2 美亚海盆空间重力异常图Fig.2 Free-air gravity anomaly of the Amerasia Basin

白色曲线为2 000 m等深线;1—罗蒙诺索夫海岭;2—马卡罗夫海盆;3—波德沃德尼科夫海盆;4—阿尔法海岭;5—门捷列夫海岭;6—楚科奇台地;7—北风脊;8—加拿大海盆;9—阿拉斯加图3 美亚海盆沉积层厚度图Fig.3 Sediment thickness of the Amerasia Basin
3 方法原理
Fullea等[7]提出的FA2BOUG法主要是为地形起伏较大的大陆地区设计的,目前已扩展到海洋区域。计算过程分三步:第一步,布格平板改正(Bullard A),将局部地形用一个密度恒定的无限横向延伸的平板近似,其厚度等于该点相对于海平面的高程;第二步,曲率改正(Bullard B),将布格平板替换为具有相同厚度的球形盖层,其表面距离为166.735 km;第三步,地形改正(Bullard C),消除周围地形对计算点的重力影响。
该方法根据计算点与地形之间的水平距离(R)将计算点周围划分为三个计算区域:内部区域、中间区域以及较远区域。并在这个计算区域内计算Bullard A、Bullard B和Bullard C的改正值。对于海洋区域,在每个区域都使用不同的算法:
1) 内部区域(R<ΔXi/2)(ΔXi为网格间距)是以计算点为中心、ΔXi为边长的正方形。计算过程主要分两步:第一步,计算一个内平顶棱柱的垂直引力,该棱柱侧向伸展与内部区域大小相等,高度与计算点的高程相等;第二步,将内部区域分为四个具有恒定斜率的象限。
2) 中间区域(ΔXi/2≤R (1) 其中:G为万有引力常数,取6.67×10-11m3·kg-1·s-2;ρc为地壳密度,取2 800 kg·m-3;ρw为海水密度,取ρw=1 030 kg·m-3;E是海平面测量的高度。 3) 在较远区域(Ri≤R 为了得到研究区更为精确的布格重力异常,需要去除研究区内沉积物的影响,计算过程如图4。北极地区沉积层厚度较大,计算沉积基底界面的重力效应时,需考虑到沉积层厚度与沉积物密度之间的关系,根据Glebovsky等[20]提供的沉积厚度与沉积层密度的关系,将沉积物分为不同厚度的10层(表1);并采用公式(2)将沉积物等效为地壳。 图4 计算过程图Fig.4 Calculation process chart 表1 沉积层厚度与平均密度的关系Tab.1 Relationship between sedimentary layer thickness and average density (2) 式(2)中:ρc为地壳密度;ρsed各层沉积物密度;Δh为沉积层厚度;hcor为等效地壳后沉降的高度,通过每层不断的叠加hcor,加上水深数据即可得到等效地形数据。 同时为了验证本研究所使用方法的可行性,同样使用Parker方法进行该地区的完全布格重力异常计算,Parker的正演公式为 (3) 其中:F表示傅里叶变换;Δg(x,y)为重力异常值;Δρ为界面之间密度差值;k为波数;Z0为平均水深值;T(x,y)为测深地形。 本节采用基于改进的FA2BOUG法并使用等效地形数据,对北极美亚海盆区域进行布格板改正、曲率改正以及地形改正后得到该区的布格重力异常值(图5(a))。为验证本文所用方法的可行性,计算了研究区未经沉积效应改正的布格重力异常值(图5(b))以及使用Parker公式分层去除水深、沉积物影响的布格重力异常值(图5(c))。 从图5可以看出,三种方法计算的布格重力异常与地形呈明显的负相关性。在美亚海盆内,三种计算方法得到的布格重力异常值同为正值,且与海底地形负相关,随着水深不断加深,异常值逐渐加大;在美亚海盆边缘,其地形变化幅度较大,三种方法计算的布格重力异常值变化趋势相似且都具有非常陡的梯度。但在数值方面,三种方法得到的结果存在明显差异,显然采用改进的FA2BOUG法得到的布格重力异常值变化范围更大,集中在-200×10-5~400×10-5m/s2,而未改进的FA2BOUG法得到的布格重力异常值范围集中在0~380×10-5m/s2,而Parker法所计算得到的布格重力异常值集中在-100×10-5~200×10-5m/s2之间。整体上,相对于图5(c)中较为平滑的异常值变化,图5(a)、5(b)的变化更加显著,与地形(图1)关系更为紧密。值得注意的是,从图5(a)、5(b)中可以明显看出位于加拿大海盆的“反S”型的重力异常带,而在图5(c)中没有显现,由此可以看出FA2BOUG方法的优越性。 图中黑色曲线为2 000 m等深线;1—罗蒙诺索夫海岭;2—马卡罗夫海盆;3—波德沃德尼科夫海盆;4—阿尔法海岭;5—门捷列夫海岭;6—楚科奇台地;7—北风脊;8—加拿大海盆;9—阿拉斯加图5 美亚海盆布格重力异常图 Fig.5 Bouguer gravity anomaly of the Amerasia Basin 为进一步验证布格重力异常计算中进行等效地形处理的必要性以及三种方法在地形起伏较大地区的差异,笔者在美亚海盆中选择了一条穿过楚科奇边缘地和加拿大海盆中的“古洋中脊”的剖面AA′(具体位置见图1),提取该剖面的水深值(图6)、沉积物厚度值(图7)以及三种方法的布格重力异常值(图8)。 从图6~8可以看出,三种方法整体趋势保持一致,与地形保持负相关关系。在地形起伏较大的地区,如楚科奇边缘地,基于改进的FA2BOUG法使用等效地形数据和未使用等效地形数据所得到的布格重力值差异不大,但与Parker法所计算得到的布格重力异常值有非常明显的数值差异。结合图7和图8可以看出,在沉积物厚度不大的地方,沉积物的重力影响较小,但随着沉积物厚度的增大,进行沉积物改正与未进行沉积物改正的布格重力异常的差值也逐渐扩大。 图6 AA′剖面水深图Fig.6 Bathymetry of the AA′ profile 图7 AA′剖面沉积物厚度图Fig.7 Sediment thickness of the AA′ profile 图8 三种方法的AA′剖面布格重力异常值Fig.8 Bouguer gravity anomoly of the three methods along AA′profile 为确定上述三种方法中深度与布格重力异常值之间的相关性,对其进行了线性拟合处理(图9),计算每种方法的拟合度R2,拟合度越高,变量之间相关性越强。由图9可知,基于改进的FA2BOUG法的两者拟合度为0.950 7,未改进的FA2BOUG法的两者拟合度为0.948 54,Parker法的两者拟合度为0.91,由此可知采用改进的FA2BOUG法获得的布格重力异常值更加优越。 鉴于此,采用改进的FA2BOUG法来计算北极美亚海盆的布格重力异常值并分析该区布格重力异常的分布特征,为后期进一步研究该区的构造特征奠定基础。计算结果显示,美亚海盆内布格重力异常变化主要集中在150×10-5~400×10-5m/s2。在加拿大海盆中,深海地区数值较大,并且由深海地区向海岸带附近逐渐变小;在马卡罗夫海盆以及波德沃德尼科夫海盆中变化幅度不大,相对来说,水深较深的马卡罗夫海盆异常值较大,达400×10-5m/s2。阿尔法-门捷列夫海岭的布格重力异常值不大,主要集中在200×10-5m/s2左右。 黑色点为剖面对应的深度、布格重力异常值,直线为线性拟合趋势线图9 深度与重力值的线性拟合图Fig.9 Linear fitting between depth and gravity value 本研究利用全球最新发布的空间重力异常数据、水深数据以及沉积层厚度数据,进行沉积物改正后,基于改进的FA2BOUG法计算该地区的布格重力异常值。在计算过程中,为了验证所选用方法的正确性,选用了经典的Parker公式逐层去除水深、沉积物影响及未进行沉积物改正的FA2BOUG方法,分别计算该地区的布格重力异常值,将三种计算结果进行比较分析。 通过比较分析,三种方法得到的结果整体变化趋势相一致,但基于改进的FA2BOUG法计算得到的布格重力异常特征与地形具有更好的相关性,尤其在地形变化较大的区域。美亚海盆的布格重力异常值主要为150×10-5~400×10-5m/s2,最大可达400×10-5m/s2;而海岭地区布格重力异常值在200×10-5m/s2左右变化。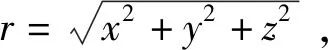

4 结果与讨论

5 结论
