基于椭圆曲线加密算法的SET协议改进研究
2020-11-12圣文顺王玉祥孙艳文
圣文顺 王玉祥 孙艳文
1(南京工业大学浦江学院 江苏 南京 211200) 2(南京信息工程大学计算机与软件学院 江苏 南京 210044)
0 引 言
电子商务统指在网络上从事的交易行为,可以用来买卖商品、信息和服务等[1]。由于全程通过互联网络操作,不受地理位置、时间等外界因素的影响,交易方式灵活,耗费的财力和人力少且交易过程简洁,所以备受人们的喜爱[2]。电子商务作为网络信息社会中一种新兴的商务模式,一直在改变着人们的衣食住行。
电子商务的核心问题是如何保证其安全性,由于所有交易环节都在网络上进行,交易双方对彼此的身份知之甚少,这使得交易过程存在一定的安全隐患[3-5]。为了更好地发展电子商务,研究人员着力于研发更为安全、高效的加密技术。
1996年2月,国际组织的两大信用卡发行商MasterCard和VISA共同商议并最终敲定安全电子交易协议,即SET协议[6]。此后,全球各大金融机构都纷纷自发地研发能够应用于SET协议的软件和相关技术。当前,SET协议已经成为全球电子交易领域的规范和标准。SET协议最适合应用于商家与消费者交易模式,可以实现三方认证,因此获得了该行业中的Microsoft、惠普、IBM和美国网景[7-9]等大型公司的支持,并通过了IETF标准的认可,成为商家与消费者模式的权威标准。MasterCard和VISA两大信用卡国际组织于1997年12月共同成立了能够在全球范围内管理与促进安全电子交易SET协议推广应用的安全电子交易有限公司。该公司被授予了一些最高等级的权利,诸如可以认定根认证机构,建立一个具有分层结构的认证系统等。
安全电子交易协议也具有一定的缺陷,例如操作过程不够简单、耗费财力过高且难以普及等,待进一步改进和提高。本文从电子商务SET协议的基本原理[10]出发,对电子支付安全体系中涉及的算法和技术都做了详细的介绍;着重分析研究椭圆曲线加密算法的基础理论框架[11];基于椭圆曲线技术对SET协议进行改进,并融合了MD5哈希生成算法[12]提高数据加密的安全性;通过大量仿真实验进行算法性能对比,验证改进后算法的优越性。
1 基于椭圆曲线的SET协议改进
1.1 基于一补数减法形式的改进算法
为了提高椭圆曲线上标量点乘kP的计算效率[13-15],提出了用二进制的补码来进行运算的改进办法,首先将整数k转换成二进制,然后用二进制位权的补数形式来表示整数k,具体实现算法如下:
1) 一补数减法形式方法。若正整数k的二进制表示为(ki-1,…,k1,k0)2,则将其转换为一补数减法[16-17]形式:
(1)
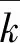
(100000000)2-(00010100)2-1=
(2)
通过上述计算结果我们可以得出,若k的二进制表示对应的汉明权[18]相比其一补数减法形式较大时,则对其进行转换是非常必要的。因为在标量乘计算中,k越大计算量就越大。
算法1一补数形式计算标量乘的算法
输入:k=(kl-1,…,k1,k0)2,P∈E(Fq)。
输出:Q=kP。
Step2If 0≤i≤l-1
Ifki=1
Q←Q+P;
Else
Q←Q-P;
Step3返回Q;
End
从上述例子可以看出,转换前后运算次数相差两次,很明显经转换后计算次数减少了近一半。将算法1称为一补数减法形式,简称CS形式。将NAF方法[19]与CS方法基于二进制长度的变化进行比较,比较结果如表1所示。

表1 不同二进制长度下NAF与CS方法运算时间对比 ms
可以看出,CS方法很明显比改进前的NAF算法要高效、快速。
2) 部分使用一补数减法形式方法。二进制表示转换成一补数减法形式具有简单、快速的优点,但是在减少二进制表示的汉明权效果上并不是对所有的标量都有效。因此,在CS方法的基础上需做进一步改进,通过特定的算法来判断是否需要进行转换以及对哪一部分进行转换,称该方法为部分使用一补数减法,简称PCS方法,如算法2所示。
算法2将二进制表示的整数转换成部分使用一补数减法
输入:k=(kl-1,…,k1,k0)2。
输出:k的PCS形式k′。
Step1i=0;
Step2Ifi≤l-3
Ifki=ki+1=1
j=i+2;
Ifj≥0
Ifkj=0
Ifj≤l-3且kj+1=kj+2=1
j=j+3;
Else跳出j≥0循环;
Elsej=j+1;
Else Ifl=((j-1)-i+1)>2
If 0≤n≤j-i
kn+i=mn;
i=j;
Elsei=j+2;
Elsei=i+1;
Step3返回k的PCS形式k′;
End
对于是否进行转换,评判标准为:如果有两个连续的“1”则进行标记以便进一步判断。即转换部分所需要满足的条件为:
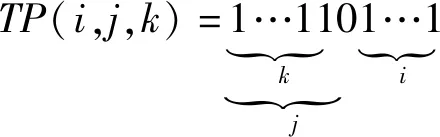
(3)
式中:i≥2,j≥0,k≥2。式(3)的含义为:如果在扫描过程中遇到两个连续的“1”则先将其进行标记,若扫描到“0”,则继续扫描“0”后面是否有两个“1”,若符合则往下扫描,否则在“0”前终止,所得结果为前面的标记部分TP(i,j,k);接下来计算TP(i,j,k)的长度,如果大于2,则进行转换,小于2则不转换。
算法3PCS形式计算标量乘的算法
输入:k=(kl-1,…,k1,k0)2,P∈E(Fq)。
输出:Q=kP。
Step1计算k的PCS形式k′;
Step2If 0≤i≤length(k′)-1
Q←2Q;
Ifki=1
Q←Q+P;
Else
Q←Q-P;
Step3返回Q;
End
下面举例说明该算法的有效性。
对于一整数1122334455,其二进制形式k为:
k=(1000010111001010111011011110111)2
(4)
转换后的表示为:
(5)
这说明用PCS形式进行转换后,计算次数明显小于二进制的情况,由此得出,改进后的PCS算法在减少计算量方面有着突出的优势。
1.2 算法改进前后比较与分析
将整数k转换成NAF的过程需要进行大量运算,始终保持k值的二进制表示不变,对PCS方法与NAF方法进行对比分析。算法4就是将二进制转换成NAF表示的算法。
算法4二进制表示转换成NAF表示的算法
输入:k=(kl-1,…,k1,k0)2。
输出:k的NAF表示k′。
Step1i=0,C0=0,kl=kl+1=0;
Step2If 0≤i≤l
{
Ci+1=[(ki+ki+1+Ci)/2];
}
Step3返回k的NAF表示k′;
End
将以上转换应用于标量乘算法中就得到了对应的标量乘算法,如算法5所示。
算法5二进制表示转换成NAF表示的标量乘算法
输入:k=(kl-1,…,k1,k0)2,P∈E(Fq)。
输出:Q=kP。
Step1计算k的NAF表示k′;
Step2Q←∞;
Step3If 0≤i≤length(k′)-1
Q←2Q;
Ifki=1
Q←Q+P;
Else
Q←Q-P;
Step4返回Q;
End
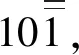
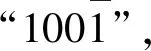
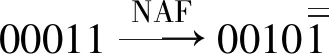
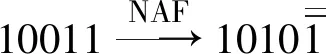
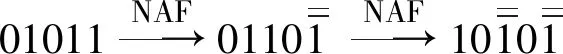
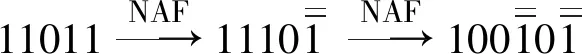
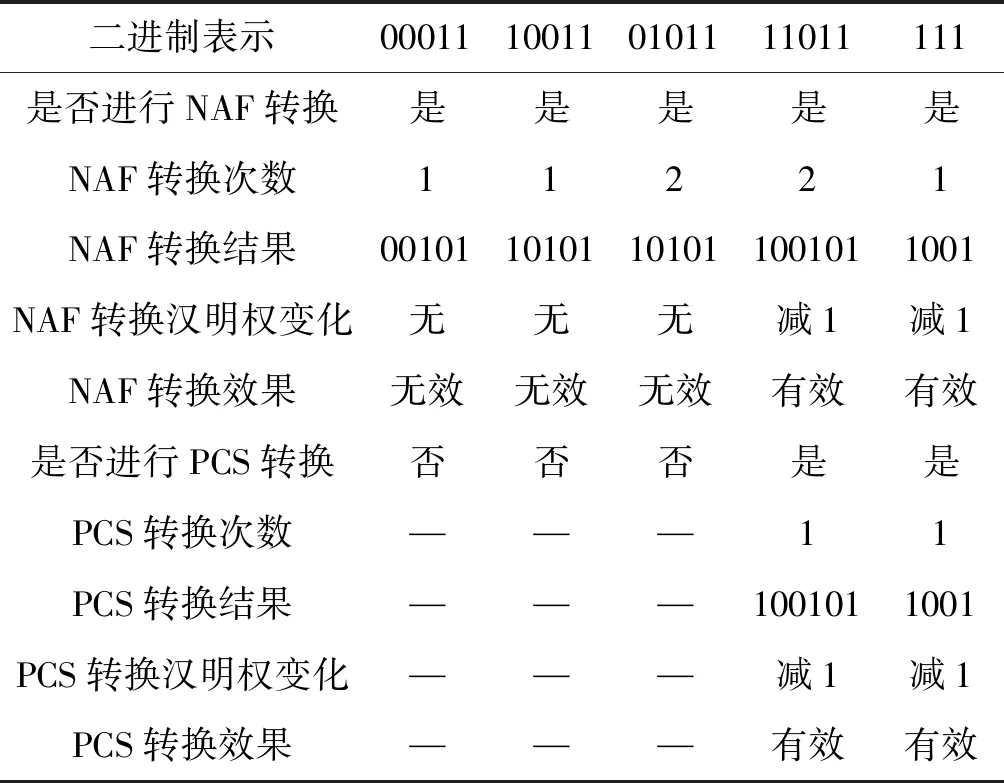
表2 NAF表示过程中的一些基本转换对比
由表2中的数据可得,相对于NAF的一些无效转换来说,PCS在减少计算量、提高算法效率方面有着明显的优势。
1.3 改进算法与MD5融合策略
将改进后的算法与MD5哈希算法进行融合,在改进后的算法中添加对信息H运用MD5算法进行128位密码的生成策略,在提高算法效率的同时确保数据的安全性。具体步骤如下:1) 信息H在进行ECC加密的同时进行MD5加密,得到128位密码;2) 在发送信息过程中,发送128位密码和信息H;3) 解密时通过ECC得到信息H,并对信息H进行MD5哈希生成算法融合;4) 对比解密得到的128位密码和接收到的密码是否一致,判断是否接受为信息H。对应流程如图1所示。
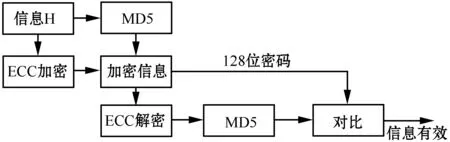
图1 融合策略流程
2 实 验
2.1 RSA和椭圆曲线加密算法对比
椭圆曲线加密技术具有高效、快速、低耗等优点[20]。对于相同的安全需求来说,椭圆曲线相比RSA[21]的计算量和消耗的时间都要少,如表3所示。
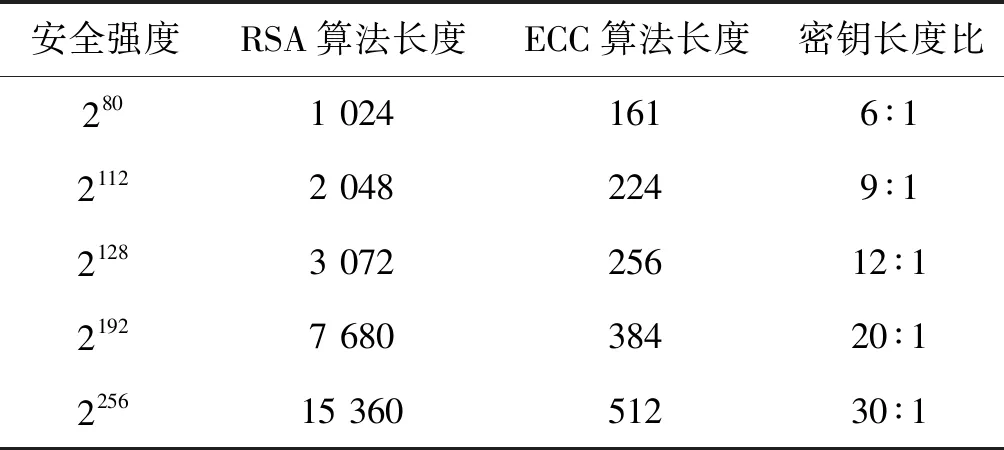
表3 相同安全强度时RSA与ECC密钥长度比较
根据表3中的数据,在MATLAB中做数据拟合得到曲线如图2所示。
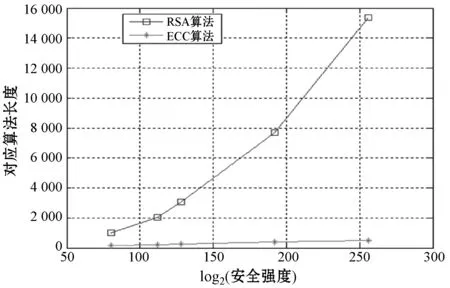
图2 RSA和ECC密钥长度的比较
可以看出,在相同的安全强度下,RSA所需要的密钥量远高于椭圆曲线所需要的密钥量。
2.2 改进前NAF与改进后PCS对比
1) 运算时间的对比。根据NAF方法和CS方法在只有二进制长度作变量情况下运算耗时的差别,本文在MATLAB中做仿真曲线实验,结果如图3所示。
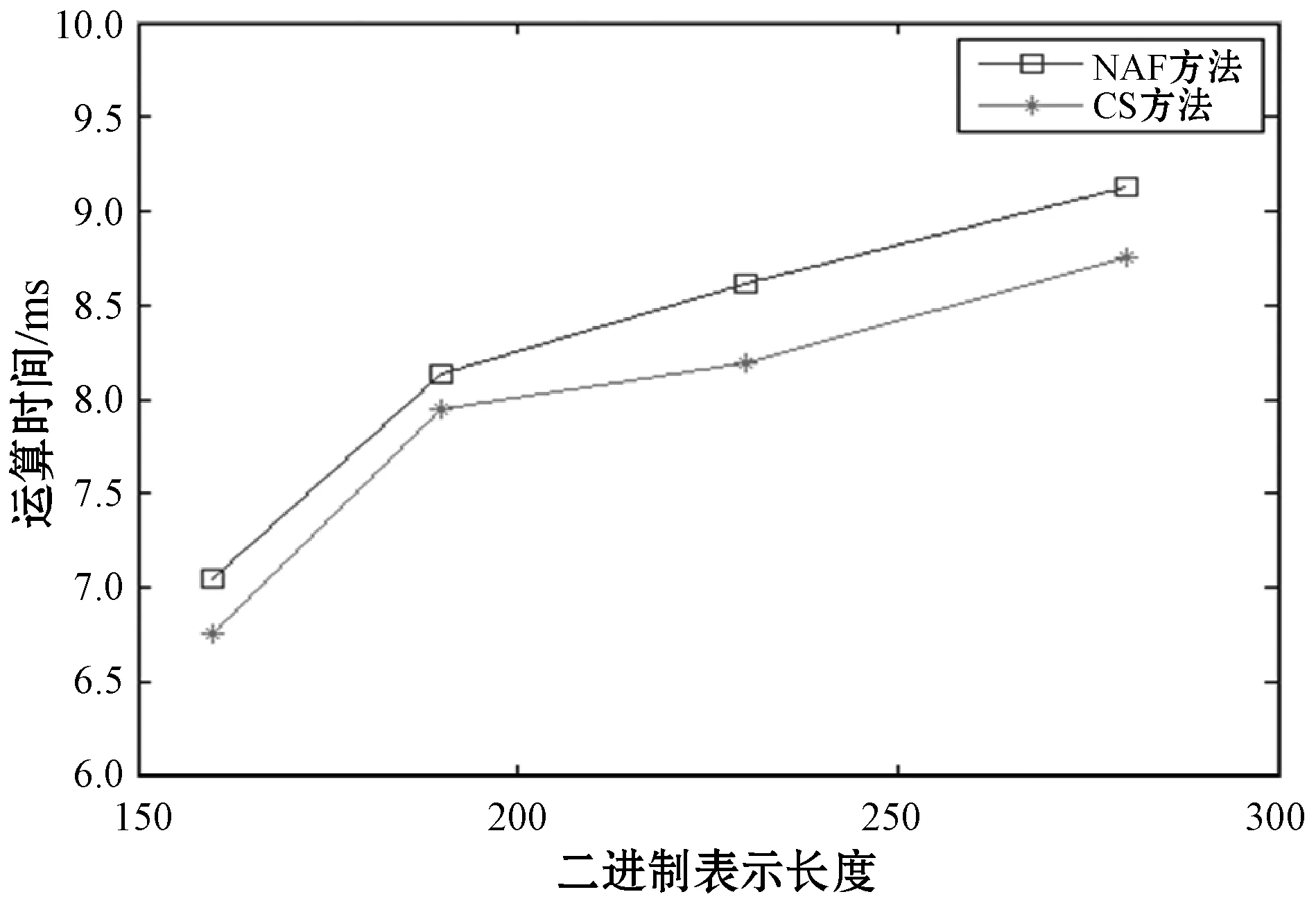
图3 NAF方法和CS方法的运算时间比较
可以看出,CS形式的优势在于它比NAF形式更省时。在算法1中,运算量只来源于位减法,而不像NAF形式需要大量的取模和除运算。因此所提出的改进算法更简单、快速。
2) 汉明权的对比。根据表2对10个不同k值在三种表示形式下的汉明权进行对比,在MATLAB中做仿真曲线实验,结果如图4所示。
可以看出,在减少汉明权方面,PCS形式和NAF表示的效果相同。这表明PCS形式在减少标量乘计算的运算量方面与NAF表示具有相同的效果。
3) 转换次数的对比。对10个不同正整数的二进制表示分别用PCS形式和NAF形式进行转换,得到转换次数的对比数据,在MATLAB中做仿真曲线,结果如图5所示。
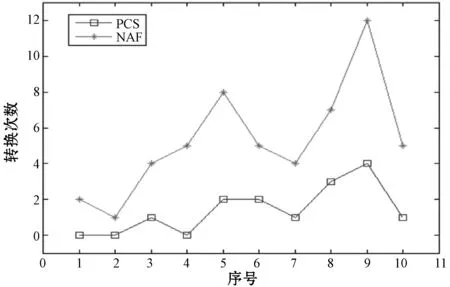
图5 不同k值的二进制表示转换成NAF形式和PCS表示的转换次数比较图
图5说明了针对不同二进制表示的k值,将其变换成NAF要比PCS的变换次数多,即NAF表示在进行转换时比PCS形式耗时更多。
尽管一般情况下采用NAF形式能够取得较好的效果,但同时会伴有一些无效的二进制转换导致大量的时间浪费。提出的PCS形式很好地解决了这一问题,只要进行转换必定会带来汉明权的减少,明显地提高了转换处理效率,从而将标量乘的处理时间大幅缩短。
2.3 融合算法性能评估
通过对样本文件进行加密解密操作,包括文件序号、文件存储大小、文件存储时间、文件内存信息和文件大小,具体信息如表4所示。
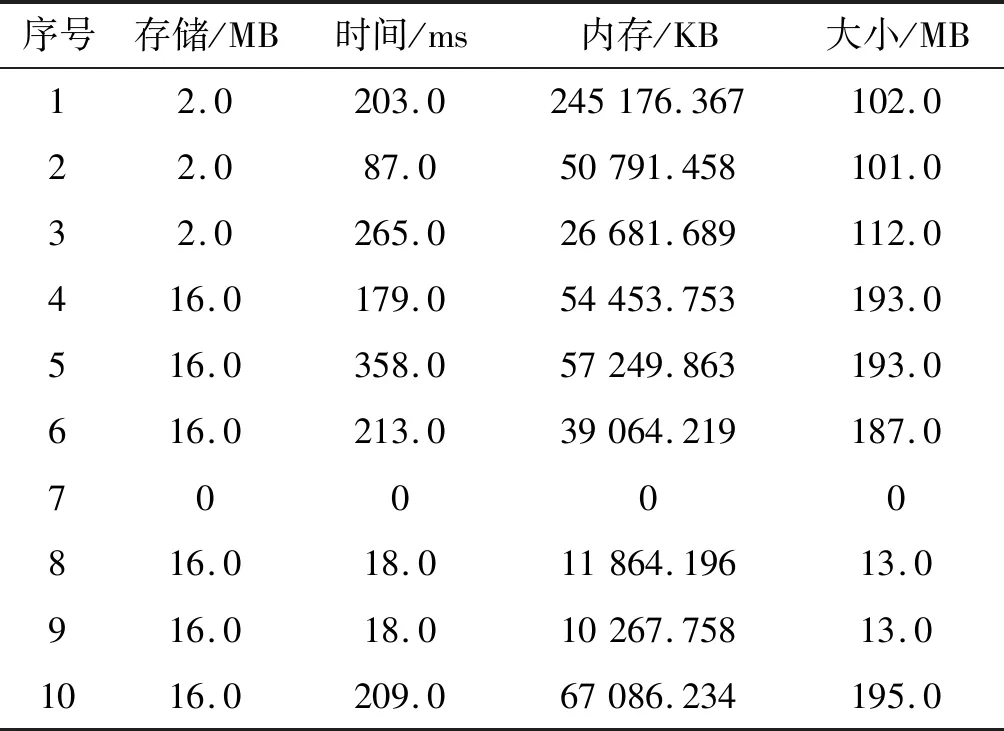
表4 文件加密时间、存储文件和文件大小
可以看出,加密以及存储大小都在合理范围内,可以有效节省内存空间以及加速加密过程,从而提高效率,验证了本文算法的优越性。
3 结 语
安全在电子商务中不容忽视。本文基于椭圆曲线加密算法对SET协议做出改进,在提高算法效率的同时融合MD5哈希生成算法进一步提高加密的安全性,并通过仿真实验多次对比加密时间和转换次数,验证了改进算法的性能及其优越性。
