不完备混合型数据的决策粗糙集与三支决策分类算法
2020-11-12王光琼
王 光 琼
(四川文理学院智能制造学院 四川 达州 635000)
0 引 言
粗糙集理论[1]是当今人工智能和知识发现领域的一种重要模型,在处理不确定性和不完备性的数据方面发挥着尤为重要的作用。传统的粗糙集模型基于等价关系建立,通过等价关系对信息系统进行划分来达到不确定性概念的粗糙近似。然而传统的粗糙集模型对噪声数据较为敏感[1-4],不具有较好的泛化能力,为了改善这一局限,提出了一种称之为决策粗糙集的模型。
决策粗糙集最早由加拿大学者Yao等[5]提出,将贝叶斯决策理论融入传统粗糙集模型中,使得其最终的粗糙近似结果具有最小的决策代价,其中决策粗糙集的上下近似通过一对阈值来限定,相比传统的粗糙集模型,该模型对噪声数据具有更好的容忍效果。在决策粗糙集模型的基础上,Yao[6]进一步地提出了三支决策理论,建立了不确定性数据环境下一种新的决策方法。为了提高决策粗糙集模型的应用范围,学者们进行了大量的改进和推广,例如:在分布式数据集下,Lin等[7]提出了一种多源信息系统的决策粗糙集模型;在不完备信息系统下,Liu等[8]提出了一种适用不完备数据的改进决策粗糙集模型;Zhao等[9]针对多值信息系统提出一种扩展的决策粗糙集;Feng等[10]提出一种变精度的多粒度决策粗糙集模型;在模糊数据的环境下,Sun等[11]提出了模糊集的决策粗糙集模型以及相关应用;Zhao等[12]在其基础上进一步地提出了模糊区间值的决策粗糙集模型;刘久兵等[13]提出了直觉模糊信息系统的决策粗糙集模型。另一方面,数值型数据也是一种常见的数据类型,Li等[14]提出了基于邻域关系的决策粗糙集模型。因此可以看出,目前决策粗糙集模型的研究已不断趋于完善。
混合性和不完备性是目前数据的一个典型特征,对于粗糙集理论,学者们对这种类型的数据也进行了广泛的研究[15-17]。然而目前的决策粗糙集模型还未对这种类型的数据进行探索,因此本文将在前人研究的基础上提出一种不完备混合型信息系统的决策粗糙集模型。
对于不完备混合型信息系统,Zhao等[15]定义了邻域容差关系,对这类信息系统进行了有效处理。本文采用邻域容差关系重新对传统的决策粗糙集模型进行重构,提出不完备混合型信息系统下的决策粗糙集模型,同时基于该模型进一步地提出相应的三支决策。此外,基于最小化决策代价的原则,本文对于所提出的决策粗糙集模型设计出一种最小化决策代价的属性约简算法。另一方面,由于三支决策提供了一种新的决策思维,本文将其融入分类模型中,提出一种不完备混合型数据的三支决策分类算法,该分类算法将样本对象的类决策结果分成三种情况,比传统的分类算法增加延迟分类的情形,即对于不确定性的样本对象进行延迟处理。仿真实验结果表明,所提出的三支决策分类算法可以有效地降低分类结果的误分类代价,提高分类精度,具有更高的分类性能。
1 决策粗糙集模型
在粗糙集理论中,数据集表示成信息系统的形式,一个信息系统可表示为S=(U,At=C∪D,V),其中:U为该信息系统S的论域,即数据集的样本空间;At为信息系统的属性集;C为条件属性集;D为决策数据集;V为整个信息系统的属性值集域,根据V中属性值的类型,通常可以将信息系统分为离散型信息系统、连续型信息系统以及混合型信息系统。通常信息系统也可简单表示为S=(U,At=C∪D)。
定义1[1]对于离散型信息系统S=(U,At=C∪D),基于属性子集B⊆C构建的等价关系EB定义为:
EB={(x,y)∈U×U|a(x)=a(y),∀a∈B}
(1)
式中:a(x)表示对象x在属性a下的属性值。根据等价关系EB,可以得到任意对象的等价类,即对象x的等价类表示为[x]B={y∈U|(x,y)∈EB}。

(2)
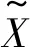
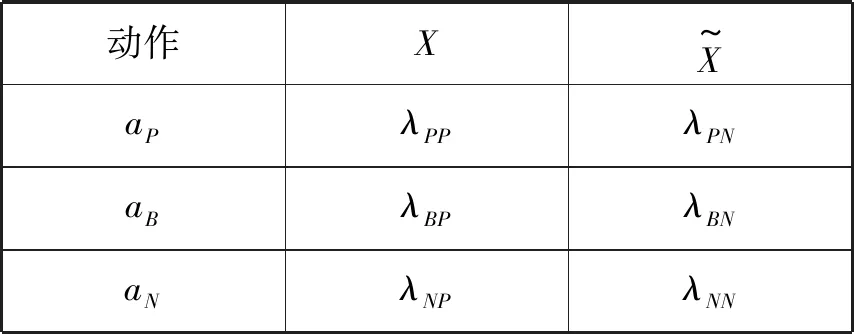
表1 决策代价
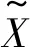
根据贝叶斯决策理论,Yao等通过最小化决策代价的原则,利用代价矩阵推导出一对阈值来进行粗糙集模型中粗糙近似的计算,使得近似的结果拥有最小的误分类代价,该模型即为决策粗糙集模型。
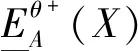
(3)
式中:θ+=max{α,β,γ};θ-=min{α,β,γ}。其中:
在决策粗糙集模型基础上,Yao等进一步地提出了三支决策模型。对于一个决策对象x,利用三支决策进行的决策行为可以描述为:
(1) 若p(X|[x])>θ+,则x判定为X;
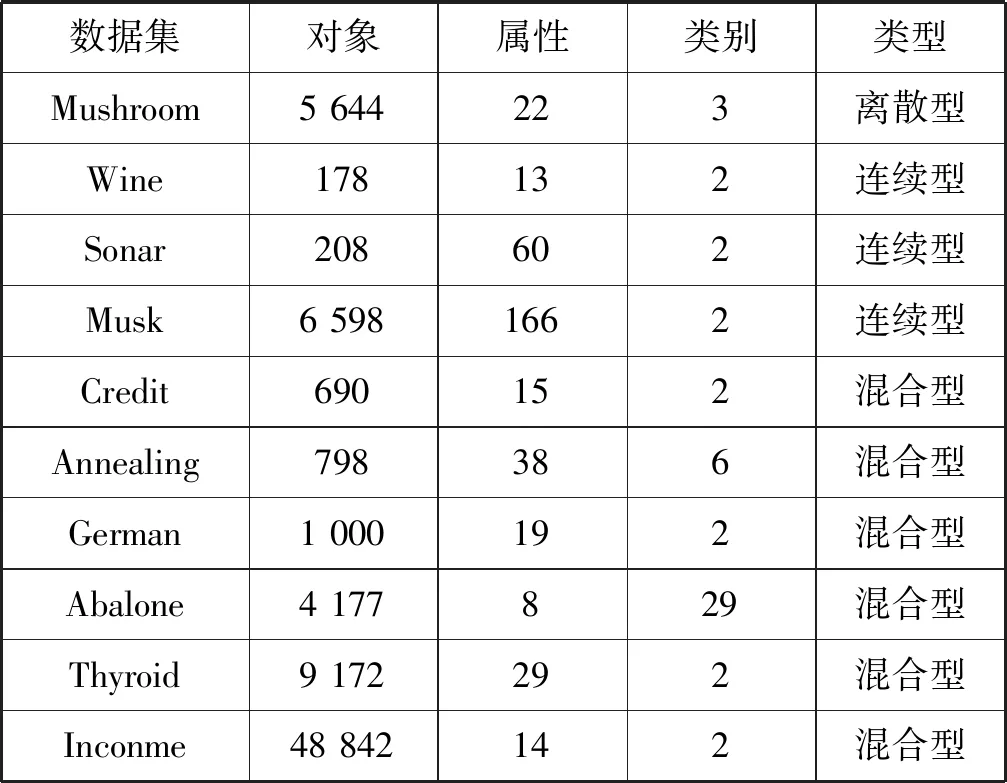
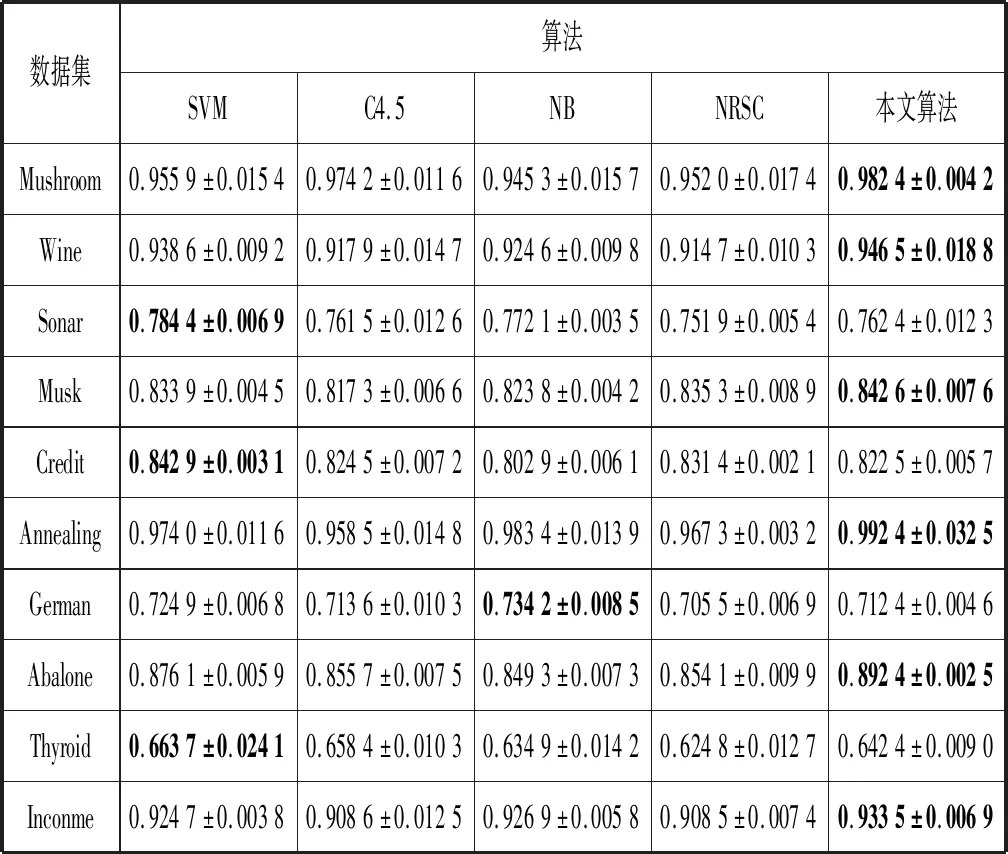
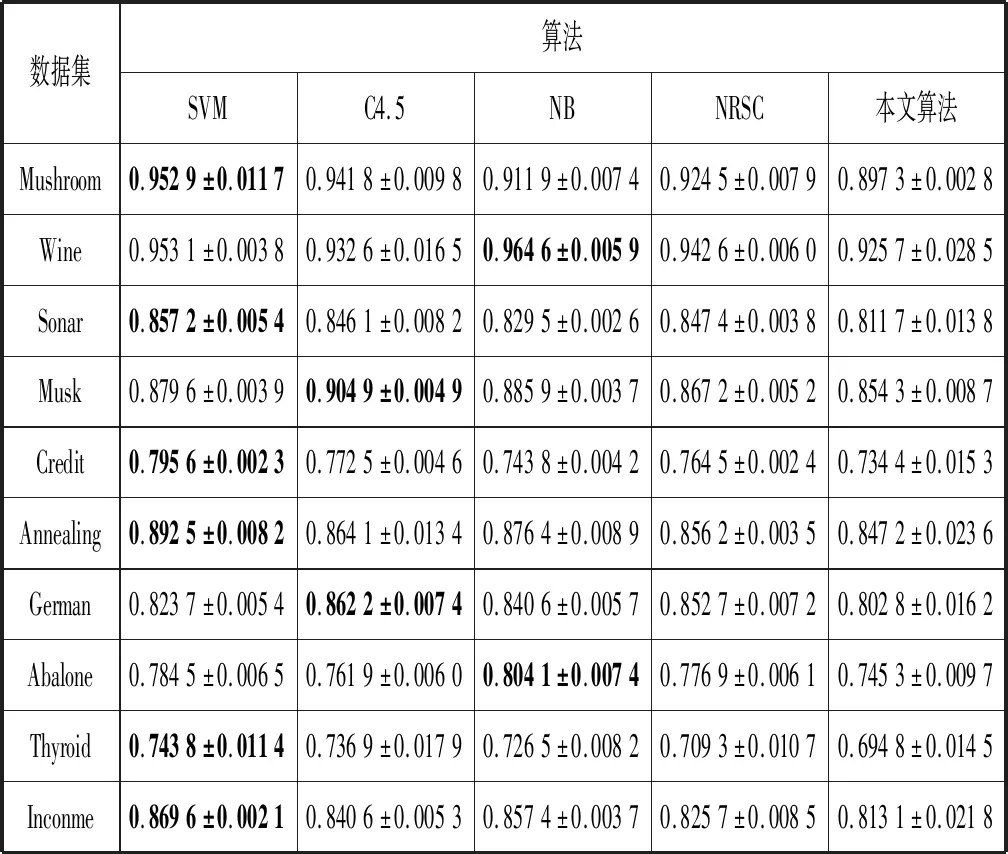
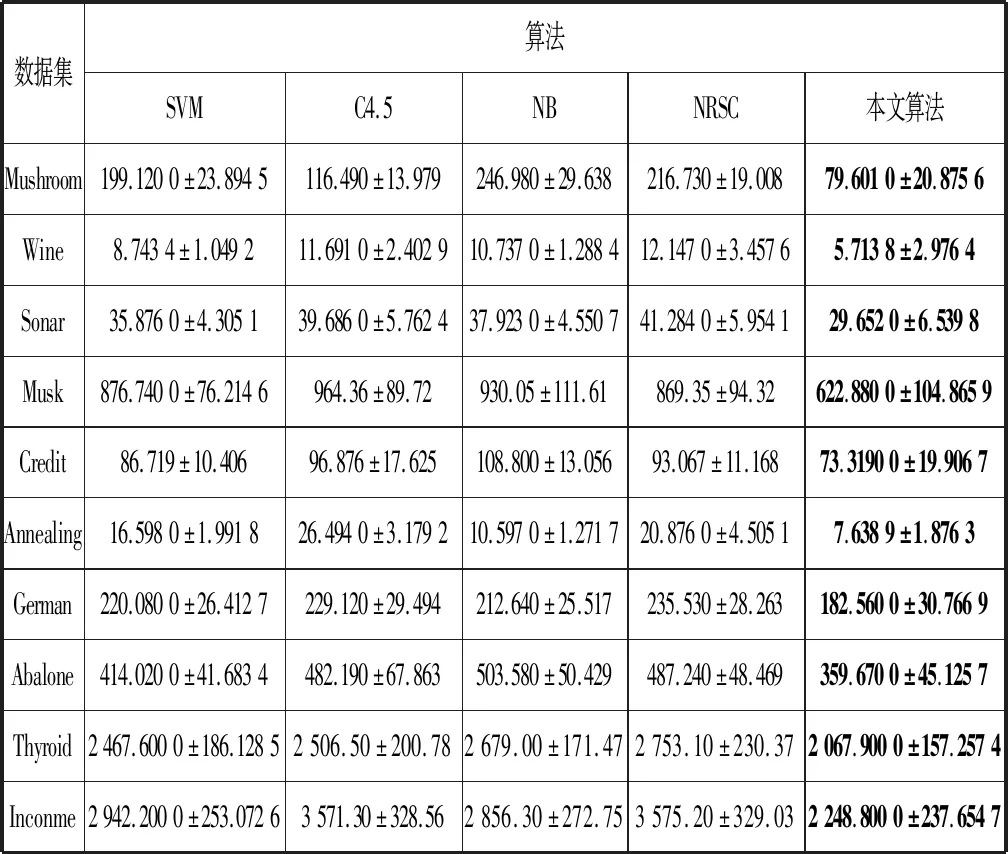
(2) 若θ- 在粗糙集理论中,传统的模型都基于完备离散型的信息系统而建立,而现实环境下的数据类型是复杂多样,不完备混合型的信息系统便是其中常见的一种。Hu等[18]通过在连续型数据下建立邻域关系,从而解决粗糙集理论对连续型以及混合型信息系统的处理。Kryszkiewicz[19]提出一种基于容差关系的扩展粗糙集模型,解决了不完备信息系统下的粗糙集近似。在两位学者的基础上,Zhao等[15]提出了邻域容差关系用于对不完备混合型信息系统的处理。 定义3[15]给定不完备混合型信息系统S=(U,AT),设属性集A⊆AT满足A=AD∪AN,其中AD和AN分别表示A下的离散型属性集和连续型属性集,那么属性集A在不完备混合型信息系统下确定的邻域容差关系定义为: ((a∈AD→a(x)=a(y))∧(a∈AN→d(x,y)≤δ))} (4) 式中:d(x,y)表示对象x与y之间的距离度量[18];δ为邻域半径,是一个非负常数;a(x)表示对象x在属性a下的属性值,a(x)=*表示属性值为缺失的情形。 根据邻域容差关系,可以对整个不完备混合型信息系统的论域诱导出一组邻域容差粒化,邻域容差粒化的结果将是不完备混合型信息系统进行粗糙逼近的基础。 (5) 同时,论域U上所有对象邻域容差类构成的集合GSA={δA(x1),δA(x2),…,δA(x|U|)}称为该信息系统的一个粒结构。显然,GSA为论域U上的一个覆盖。 在Zhao等提出的邻域容差关系基础上,将经典的决策粗糙集进行推广,提出不完备混合型信息系统下的决策粗糙集模型,同时相应的三支决策也被提出。 在邻域量化容差关系中,将对象x∈U的邻域容差类δ(x)看成与该对象属于同一类的对象集,因此在不完备混合型信息系统中,对于一个对象x隶属于某个对象集X的概率可表示为: (6) 基于该定义框架,本文构造了不完备混合型信息系统的决策粗糙集模型以及相应的三支决策。 (7) 因此,可以得到如下三种最小代价规则: POSδ(X)、BUNδ(X)和NEGδ(X)分别表示X的δ正区域、边界域和负区域。 所以,可以进一步得到: λPP·p(X|δ(x))+λPN·(1-p(X|δ(x)))≤ λBP·p(X|δ(x))+λBN·(1-p(X|δ(x)))⟹ 且: λPP·p(X|δ(x))+λPN·(1-p(X|δ(x)))≤ λNP·p(X|δ(x))+λNN·(1-p(X|δ(x)))⟹ λBP·p(X|δ(x))+λBN·(1-p(X|δ(x)))≤ λPP·p(X|δ(x))+λPN·(1-p(X|δ(x)))⟹ 且: λBP·p(X|δ(x))+λBN·(1-p(X|δ(x)))≤ λNP·p(X|δ(x))+λNN·(1-p(X|δ(x)))⟹ λNP·p(X|δ(x))+λNN·(1-p(X|δ(x)))≤ λPP·p(X|δ(x))+λPN·(1-p(X|δ(x)))⟹ 且: λNP·p(X|δ(x))+λNN·(1-p(X|δ(x)))≤ λBP·p(X|δ(x))+λBN·(1-p(X|δ(x)))⟹ 这里令: (8) 则有: (1) 若p(X|δ(x))≥α且p(X|δ(x))≥γ,那么x∈POSδ(X); (2) 若p(X|δ(x))≤α且p(X|δ(x))≥β,那么x∈BUNδ(X); (3) 若p(X|δ(x))≤β且p(X|δ(x))≤γ,那么x∈NEGδ(X)。 特别地,若代价函数满足如下关系: 那么此时有0≤β<γ<α≤1,则上述三个规则即为: (1) 若p(X|δ(x))≥α,则x∈POSδ(X); (2) 若β≤p(X|δ(x))≤α,则x∈BUNδ(X); (3) 若p(X|δ(x))≤β,则x∈NEGδ(X)。 根据以上推导的这三条规则,可以直接得到不完备混合型信息系统下的决策粗糙集模型,同时也蕴含了不完备混合型信息系统下三支决策。 (9) (10) (11) 另一方面,根据本文所提出决策粗糙集模型的三个区域划分,这里便得到了不完备混合型信息系统下的三支决策。对于目标决策结果X和待决策的对象x,那么: (1) 若对象x满足目标决策结果X的决策条件,即p(X|δ(x))>θ+,那么接受对象x判定为X,即x∈POSθ+(X); (2) 若对象x不满足目标决策结果X的决策条件,即p(X|δ(x))<θ-,那么拒绝对象x判定为X,即x∈NEGθ-(X); (3) 若对象x不确定是否满足目标决策结果X的决策条件,即θ-≤p(X|δ(x))≤θ+,那么延迟对象x的判定,即x∈BUN(θ-,θ+)(X),待得到更多信息后再进行确定。 (12) (13) (14) 证明: 因此(1)成立。 (3) 由于: 综合(1)、(2)可以得到: 因此(3)成立。 证毕。 性质1表明了本文所提出决策粗糙集三个区域的单调性。基于三支决策的视角,性质1中的式(12)表明当决策的接受阈值θ+越大,即接受的决策条件越为苛刻,那么最终可接受的对象越少。式(13)表明当决策的拒绝阈值θ-越小,即拒绝的决策条件越为苛刻,那么最终拒绝的对象越少。式(14)表明接受决策阈值越大且拒绝决策阈值越小时,即接受决策和拒绝决策都比较严格时,那么延迟决策的程度就比较宽松。相反,接受决策阈值越小且拒绝决策阈值越大时,即接受决策和拒绝决策都比较宽松时,那么延迟决策的程度就比较严格,这表现出了两种不同的决策态度。由于决策粗糙集中的阈值θ-和θ+直接由分类代价矩阵直接确定,那么代价的取值不同就决定了三支决策的决策态度。 属性约简是粗糙集理论的重要研究内容,在决策粗糙集模型中,基于最小代价的属性约简是目前的研究热点[20-22]。 (15) 基于最小化代价的属性约简定义如下: 定义7给定不完备混合型决策信息系统为S=(U,AT=C∪D),设邻域半径为δ,由决策代价确定的一对阈值分别为θ-和θ+。若属性子集A⊆C是该信息系统的最小代价属性约简,那么当且仅当: (1)CostA≤CostC; (2) ∀A′⊂A,CostA′>CostA。 在定义7中,条件(1)表明属性约简集的决策代价小于属性全集的决策代价;条件(2)展示了属性约简集决策代价的极小性,即属性约简集的决策代价在所有属性子集中是最小的。 启发式搜索是寻找信息系统约简集的一种常用方法,其中启发式函数的构造是该方法的核心。本节将通过决策代价Cost构造出一种属性约简的启发式函数。 给定不完备混合型决策信息系统为S=(U,AT=C∪D),设属性集A⊆C,对于∀a∈A关于属性集A的属性重要度定义为: (16) 利用sigA(a)作为启发式函数设计出的最小代价属性约简算法如算法1所示。 算法1不完备混合型信息系统下决策粗糙集模型的最小代价属性约简 输入:不完备混合型信息系统S=(U,AT=C∪D);决策代价矩阵C,邻域半径δ。 输出:属性约简集R。 步骤1初始化R=∅。 步骤2对于∀a∈C,计算a的属性重要度sigC(a),并将属性集C按照属性重要度从大到小进行排序,排序后的属性集记为C′。 步骤3选择属性集C′中属性重要度最大的属性at,若CostR∪{at}>CostC,那么进行C′←C′-{at}且R←R∪{at},并重新进入步骤3,若CostR∪{at}≤CostC,那么R←R∪{at}并进入步骤4。 步骤4对于属性集∀r∈R,若满足关系CostR-{r}≤CostR,那么进行R←R-{r}。 步骤5返回结果R。 Hu等[23]通过邻域粗糙集模型构造出了混合型数据的邻域分类算法,实验证明该算法具有较好的分类效果。本文在该分类算法的基础上,将三支决策思想融入其中,提出基于三支决策方法的数据分类模型。 三支决策是在经典的贝叶斯决策模型基础上的推广,它将决策对象的决策结果分成三个部分,分别为接受、拒绝和延迟,确定这三种决策结果则通过决策粗糙集模型中的阈值θ-和θ+来实现。把数据的分类也看成对数据类别的决策,因此利用三支决策模型来用于数据的分类,可以描述成如下形式: 对于二分类问题,设一个训练样本集为Data,其中样本包含两种类别,分别记为正类别和负类别,并且Data中正类别样本集表示为D+,负类别样本集表示为D-。对于一个待标记类别的样本对象x,δ(x)为对象x在样本集Data中的邻域类,那么基于三支决策模型对象x的判定规则为: (1) 若p(D+|δ(x))>θ+,x判定为正类别; (2) 若p(D+|δ(x))≤θ-,x判定为负类别; (3) 若θ- 对于多分类情形,可以不断将其转换成多个二分类问题进行处理,因此基于三支决策模型的多分类判定规则为: (1) 若p(Dmax|δ(x))>θ+,x判定为Dmax; (2) 若p(Dmax|δ(x))≤θ-,x不判定为任何类; (3) 若θ- 根据如上判定规则,不完备混合型信息系统的三支决策分类算法如算法2所示。 算法2不完备混合型信息系统的三支决策分类算法 输出:对象x的类别。 步骤1根据决策代价矩阵C计算决策阈值θ-和θ+。 步骤2根据算法1对原信息系统S进行最小化代价属性约简,得到约简结果R。 步骤3计算对象x在论域U中属性集R下的邻域类δR(x)。 步骤4判断p(Dmax|δR(x))与θ+之间的关系: 1) 若p(Dmax|δR(x))>θ+,那么x判定为Dmax; 2) 若θ- 3) 若p(Dmax|δR(x))≤θ-那么x不判定为任何类。 步骤5返回对象x的类别。 表2为实验中所使用的数据集,这10个数据集均来源于UCI机器学习数据库,其中:Mushroom为只包含离散型属性的数据集;Wine、Sonar和Musk为只包含连续型属性的数据集;其余为混合型属性的数据集。部分数据集为完备型的数据集,本实验选择其中5%的属性值进行删除,从而构造出不完备的数据集,同时,为了避免连续型属性量纲带来的影响,在实验前将所有数据集的连续型属性标准化至[0,1]区间。 表2 实验数据集 在本文提出的三支决策分类算法中,决策代价矩阵发挥着很重要的作用,实验采用在[0,1]之间取随机值的方法进行选取,选取的决策代价满足如下关系: (17) 本实验将所提出的三支决策分类算法与支持向量机分类算法(SVM)、决策树分类算法(C4.5)、朴素贝叶斯分类算法(NB)和邻域粗糙集分类算法[23](NRSC)进行实验比较,其中比较结果通过分类精度Acc、F度量和误分类MCost代价来体现,计算式表示为: (18) 式中:nPP表示被分类正确的对象数;nNP表示被错误分类的对象数;nBP表示被待定的对象数。 在本文所提出的三支决策分类算法中,邻域半径是一个较为关键的参数,它的取值不同对最终的实验结果将产生很大的影响,因此在进行实验之前需要对邻域半径的大小进行确定。由于连续型属性已标准化至[0,1]区间,本实验将邻域半径δ在区间[0,0.3]中以0.02为间隔分别进行取值,将选取的每个值对所有数据集进行十折交叉分类,这样便得到对应的分类精度结果。图1为每个数据集在不同邻域半径下得到分类精度结果。 图1 不同邻域半径下各个数据集的分类精度 观察图1的实验结果,可以发现当邻域半径选取为0.10时可以得到较好的分类结果,因此本实验选择δ=0.10进行实验。 表3为本文的三支决策分类算法与SVM、C4.5、NB和NRSC算法对每个数据集通过十折交叉法得到的分类精度Acc,结果通过“均值±标准差”来表示,最高的分类精度已用粗体表示。观察表3的实验结果可以发现,本文算法在大部分数据集下拥有最高的分类精度;SVM在少部分数据集下拥有最高的分类精度,例如数据集Sonar和Credit;NB算法在数据集German中拥有最高的分类精度。因此本文算法具有更高的分类准确度,这主要是由于分类机制的差异导致的。SVM拥有较好的分类性能,但是它是一种二支分类模型,即对象的分类的结果只有两种,标记为特定的类或不标记为特定的类,对于处于类之间的对象,可能会出现误分类情形。而本文算法对于确定的对象直接进行分类,对于类与类之间的模糊对象,通过进行延迟处理的方式,减少误分类的情况,因而在大部分数据集下拥有更高的分类精度。 表3 分类精度Acc比较结果 表4给出了三支决策分类算法与SVM、C4.5、NB和NRSC算法对每个数据集进行分类的F度量结果,其中最高的结果值已用粗体表示。观察表4可以发现,SVM分类算法在大部分数据集下拥有最高的度量值,而本文算法在所有数据集中都拥有较小的F度量结果,这主要是由于参与比较的分类算法对待分类的对象都进行了具体的类别判定,不存在延迟判定的情况,即nBP=0,因此Cov始终等于1,而本文算法会对有的对象进行延迟判别,因而nBP≥0,那么Cov≤1,因此F值会偏小。 表4 F度量比较结果 表5为所有算法对每个数据集分类结果的误分类代价MCost比较结果,其中最低的误分类代价MCost已用粗体表示。观察表5可以发现,本文算法在所有的数据集下都拥有最小的误分类代价,其他分类算法的误分类代价都高于本文算法。主要原因是本文算法增加延迟分类的判别结果,处于类边界的对象进行延迟决策,减少误分类的情况,而其他传统的分类算法对这类情形可能会将判别对象分类入其他错误的类,而进行延迟分类的代价要小于错误分类的代价,因此本文算法的误分类代价要更小。 表5 误分类代价MCost比较结果 综合实验结果表明,本文提出的三支决策分类算法在不完备混合型数据下具有较好的分类效果。 决策粗糙集是目前粗糙集理论研究的重点模型。由于现实应用环境下数据往往都是不完备混合类型,本文将传统的决策粗糙集模型进行推广,提出不完备混合型信息系统下的决策粗糙集模型,构建该模型框架下的三支决策,并设计出该模型的一种最小化代价属性约简算法。基于所提出的三支决策,提出一种不完备混合型数据的三支决策分类算法。实验分析表明,所提出的三支决策分类算法比其他传统的分类算法具有更高的分类精度、较小的误分类代价和更高的优越性。动态性也是现实数据集的重要特征,因此接下来将进一步研究不完备混合型数据决策粗糙集的增量式学习问题。
2 不完备混合型信息系统下的决策粗糙集模型
2.1 邻域容差关系
2.2 模型设计



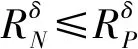
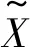
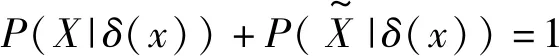

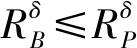
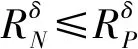
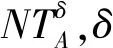
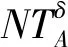
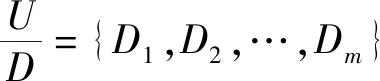
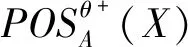
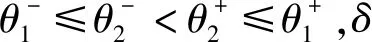
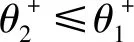
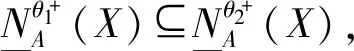
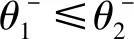
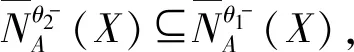
2.3 属性约简
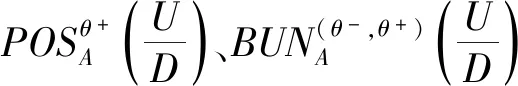
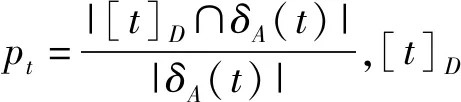
3 不完备混合型信息系统的三支决策分类算法
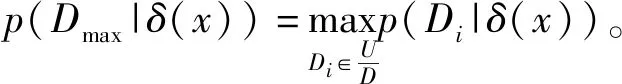
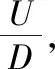
4 实 验
4.1 实验设置
4.2 邻域半径的选取
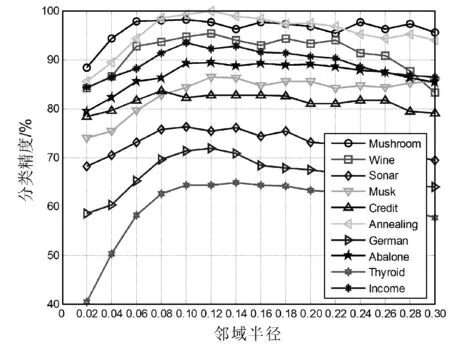
4.3 结果分析
5 结 语
