一种基于DSOGI的三相不平衡电网锁相环研究与仿真

贾 强，张显才，吴胜华，张 丰

（1.空军预警学院雷达士官学校，湖北 武汉 430345；2.空军预警学院，湖北 武汉 430014）

0 引 言

随着目前新能源技术和电力变换设备的不断发展，需要对电网电压的幅值、频率以及相位等进行精确跟随检测，从而为控制环节的设计提供同步参考信号。锁相环（Phase Locked Loop，PLL）技术作为实现这一功能最主要的方式，得到了广泛研究和应用[1-3]。这一技术在三相平衡电压中较易实现，但实际的电网电压存在一定畸变，对锁相环技术提出了更高要求[4-5]。

目前较为常用的是基于旋转坐标系的锁相技术。这种技术在电网平衡状态下各方面性能都比较优越，可对于不平衡电网，会在dq轴上产生二次谐波，对幅值、相位信息提取的准确性产生较大影响[6]。为解决这一问题，文献[7]提出了一种解耦双同步旋转坐标系锁相环，通过解耦网络将正负序分量解耦，一定程度上消除了二次谐波的影响，但使用滤波器较多，实现较复杂。文献[8]引入自适应观测器进行相位锁定，但涉及大量的编程和算法，实际实现起来对硬件要求较高。文献[9-11]引入二阶广义积分作为锁相环正交信号发生环节，并对其进行改进，能消除负序谐波对正序分量的影响，尤其是在不平衡电网电压中应用，能实现相位信息的精确检测，得到了国内外学者的广泛研究。

本文在阅读大量国内外文献的基础上，通过三相矢量分析、工作原理分析、关键环节设计以及仿真分析验证等步骤，研究一种应用于三相不平衡电网时的基于双二阶广义积分的锁相环的设计及实现方法，从而为后续学者研究相关内容提供一定的参考借鉴。

1 不平衡电网的三相矢量分析

考虑n次谐波分量的三相不平衡电网电压可分解为：

经过Clark变换，可将自然坐标系变换至αβ静止坐标系，得：

其中，Tαβ为Clark坐标变换矩阵。经过Park变换，可将αβ静止坐标系变换至dq同步坐标系，得：

其中，Tdq为Park坐标变换矩阵[12]。

联立式（2）和式（3），可以推导出三相电压矢量的相位表达式：

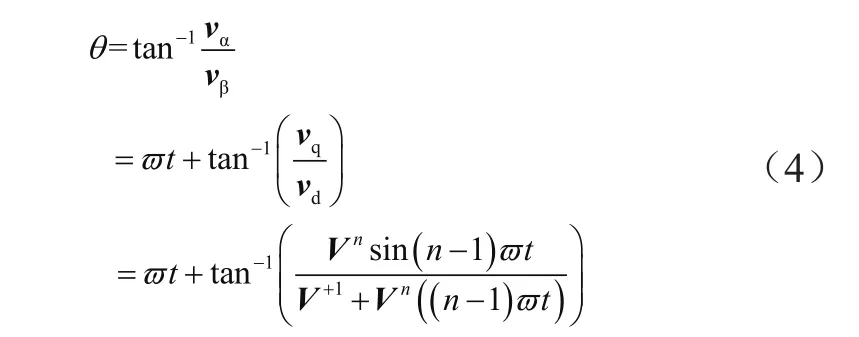
三相电压矢量的幅值表达式为：

从式（5）可以看出，含有n次谐波的不平衡电网的电压相位和幅值都受到谐波分量的影响而产生较大变化，为锁相环设计带来了很大困难。

2 DSIGO锁相环工作原理

目前，基于双二阶广义积分的锁相环结构甚多，但对三相不平衡电网呈现出的锁相环节也参差不齐。仿真分析验证，本文研究的锁相环对三相不平衡电网具有较高的跟随精度，准确性也较高。

本文研究的基于双二阶广义积分的锁相环结构原理，如图1所示。该系统主要由Clark变换、正交信号发生环节（Quadrature Signal Generator，QSG）、正负序分量提取环节及频相检测环节等部分构成。三相电压先经过Clark变换将自然坐标系下的三相电转换至αβ静止坐标系，后经过由两个二阶广义积分器构成的正交信号发生环节，使正、负序电压产生90°相移，之后由正负序分量提取环节分离出电压的正序分量和负序分量，再经过包含Park变换和PI控制器的频相检测环节，最终实时三相电网电压的幅值、相位以及频率信息进而，达到锁相的目的。

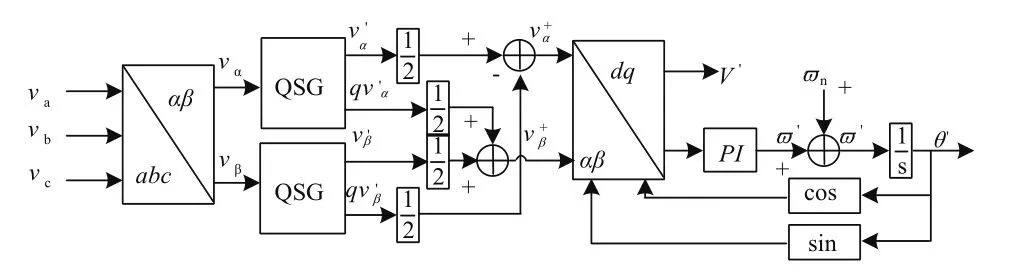
图1 基于双二阶广义积分的锁相环结构框图

3 DSIGO锁相环关键环节设计

目前虽就三相电压的坐标变换比较成熟，但本文研究的基于双二阶广义积分的锁相环系统还包含几个比较关键的环节，在设计过程中需要格外注意。

3.1 正交信号发生环节设计

正交信号发生环节主要作用是实现正、负序电压实现90°相移，为后续的正负序分量提取打下基础。目前，常用的基于传输延时的正交信号发生环节实时性能较差，不能很好地实现相位跟随锁定，有些也不能适用于不平衡电网。本文研究的基于二阶广义积分的正交信号发生环节如图2所示。图2中，v′和qv′为一对正交信号，相位相差90°，ϖ′为输出锁相角频率。

图2 正交信号发生环节结构框图

该结构的传递函数为：

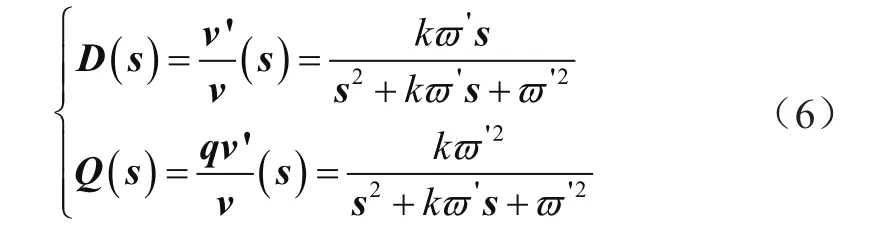
式中，k为阻尼系数，ϖ′谐振频率。对于380 V/50 Hz电压，ϖ′=100π。令s=jϖ，可得式（6）的幅频特性和相频特性分别为：

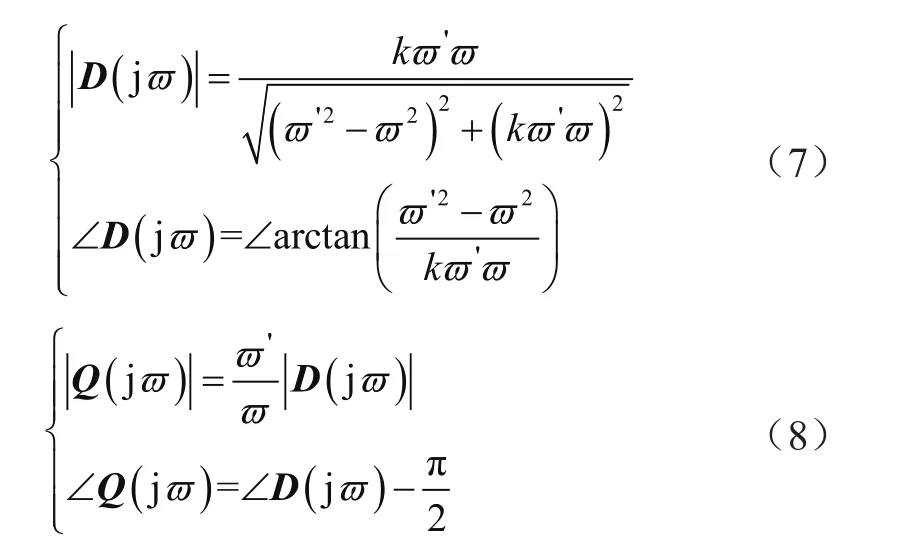
可以看出，当 |Q(jϖ)|=|D(jϖ)|=1时，∠D(jϖ)=0℃，∠Q(jϖ)=90℃，该基于二阶广义积分的正交信号发生环节可以很好地产生正交信号。

图3、图4为不同k值时传递函数D(s)、Q(s)的幅频、相频特性曲线。从频率特性曲线可以看出，当k取值过大时，滤波性能更优，更有利于选取基波频率，但带宽会随之下降。为了兼顾滤波效果和频带宽度，此次设计中k选取为1.414。

图3 不同k值时D(s)的频率特性

3.2 正负序分量提取环节设计

三相不平衡电网电压除了分解为式（1）以外，还可以分解为正、负、零序分量相叠加的形式：

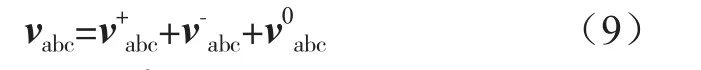
其中：

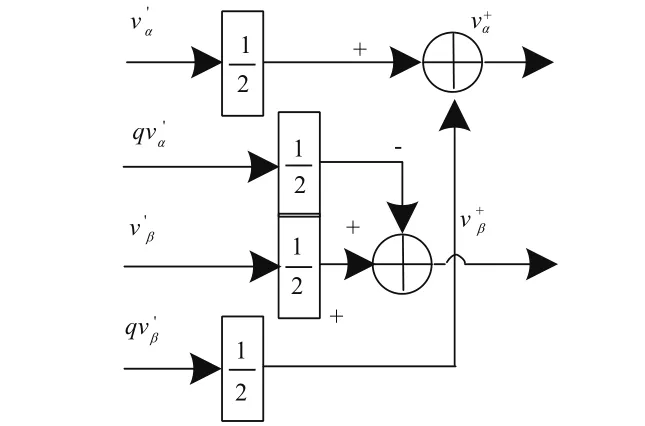
图5 正负序分量提取环节结构框图

3.3 频相检测环节设计

频相检测环节如图6所示，将正负序分量提取环节提取出的正、负序信号经过Park变换至dq同步旋转坐标系中，对q轴分量进行PI控制，便可改变频相检测的动态响应。经过对该部分结构的波特图分析，选取Kp=1、K1=1×10-3时，设计具有较好的动态特性。

图6 频相检测环节结构框图

4 仿真结果分析

为验证本文研究的基于双二阶广义积分的锁相环系统结构及参数的可行性，在电力电子仿真软件PLECS中搭建仿真模型，分别就平衡三相电网电压、两相跌落三相电网电压以及三相注入4%三次谐波的电网电压3个方面进行仿真讨论。

图7为三相平衡电网时的输入电压、正负序电压分量、输出频率、输出频率误差及输出相位。可以看出，该锁相环输出频率稳定在50 Hz，输出频率误差为0 Hz，输出相位稳定，能精准实现三相平衡电网的频率、幅值以及相位锁定。

图7 输入三相平衡电网时的仿真结果

图8为a、b两相跌落至200 V时的仿真结果。可以看出，系统经过0.048 s后保持稳定，输出频率稳定误差为±0.002 V，输出相位稳定误差为±0.005 rad/s，误差较小，说明研究的锁相环能适用于两相电压跌落的不平衡电网锁相。

图8 输入两相电压跌落时的不平衡电网时的仿真结果

图9为三相均注入4%三次谐波时的仿真结果。可以看出，系统经过0.01 s后保持稳定。谐波电压的存在，对正、负序分量均产生影响，产生±5 V的上下波动，致使输出频率产生±0.08 Hz的上下波动，输出相位产生±0.005 rad/s的上下波动，但相比传统的锁相环仍体现出了较高的精度，说明研究的基于双二阶广义积分的锁相环能适用于含有一定谐波分量的不平衡电网锁相。

图9 注入4%三次谐波时的不平衡电网时仿真结果

5 结 论

本文针对传统锁相环在不平衡电网中应用时锁相精度不高、抗干扰能力弱的问题，研究了一种基于双二阶广义积分的锁相环系统。阐述该系统的工作原理，就其关键环节进行设计并进行仿真验证。仿真结果显示，该锁相环能实现平衡电网精准锁相，在不平衡电网时锁相误差较小，精度较高，能满足三相不平衡电网电压锁相，具有一定的实用价值。