一种低成本高可靠性的SPMSM启动方法

范立荣，黄景鹏

（广东交通职业技术学院 汽车与工程机械学院，广东 广州 510650）

0 引 言

PMSM由于没有转子绕组，故体积小、重量轻、效率高、惯量小且控制精度高，同时保留了普通直流电动机优良的机械特性[1]，使其广泛应用于各个行业。对永磁同步电机的控制主要为矢量控制，可以准确控制转矩与转速。近期有不少电机控制系统采用直接转矩控制，但在转矩和磁链的控制方面不尽如人意[2]，因此选择采用矢量控制。

PMSM多种控制的最终思想是将电枢与励磁磁场分隔并解耦，从而使得电机的转矩分量和励磁分量可独立控制[3]。目前，PMSM矢量控制最常见的5种控制方式分别为[4]id=0的控制、转矩电流比最大控制MTPA、cosφ=1控制、最大输出功率控制以及弱磁控制。

IPMSM大多采用MTPA结合弱磁的方式进行控制，而SPMSM中由于Ld=Lq存在转矩公式：

从式（1）可以看出，电磁转矩和q轴电流及永磁体磁链强度有关。永久磁链在外施电压一定时是一个常数，此时控制电流iq可控制Te。这样的控制比IPMSM采用MTPA结合弱磁的控制方式简单高效。因此，本文采用id=0的控制方式对SPMSM进行控制并仿真。

1 SPMSM矢量位置观测器

1.1 位置观测器状态矢量方程

永磁同步电机在旋转参考系（SRF）d-q轴上的电压方程为：

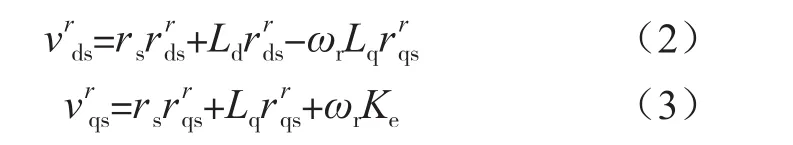
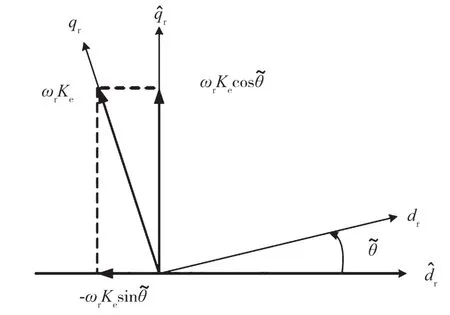
图1 旋转坐标系下d-q轴电压及反电动势电压矢量图

假设实际转子角度和估算转子角度之间的误差足够小，那么可以忽略实际旋转坐标系和估算坐标系上d轴电感与q轴电感之间的差异。d-q轴上的电压方程表示如下：

结合式（1）～式（7），可以得到电子电压空间状态矢量方程如下：

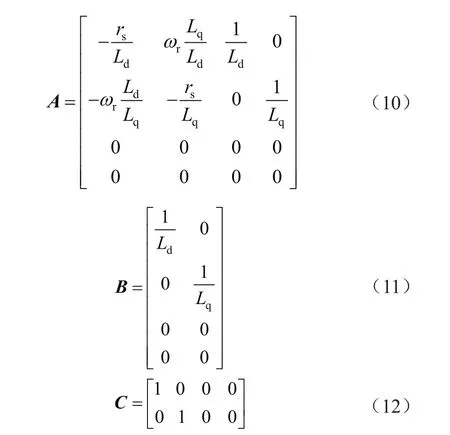
由于电机的机械时间常数通常比电气的时间常数大很多，因此与电机的电流和电压相比，旋转频率和电动机速度的变化较慢。

1.2 状态矢量方程求解

从式（8）和式（9）可以得出：

由矩阵的特性可知，式（13）矩阵是可观测性的，且是奇异的。因此，式（8）和式（9）也是线性可观测的时变系统。可根据输出变量d轴和q轴电流估算第三和第四状态变量，或通过估算d轴和q轴的反电动势电压估算转子的转子角度和角频率。为了验证算法的有效性，在MATLAB/Simulink系统搭建无位置速度矢量模型并进行仿真。

2 MATLAB/Simulink模型搭建

系统采用的无位置速度传感器矢量结构由转速电流双闭环系统构成。外环为转速环，内环分为Id电流环和Iq电流环，分别控制磁场和电磁转矩。转子角度θest和ωest的估算可利用系统采样电机定子电流变换得到的Vα、Vb、Iα以及Iβ。系统采用idref=0的控制方式，采用状态空间矢量控制进行位置估算，系统整体运行结构如图2所示。

对应图2搭建的MATLAB/Simulink仿真模型如图3所示。

图2 SPMSM状态观测器矢量控制系统框图

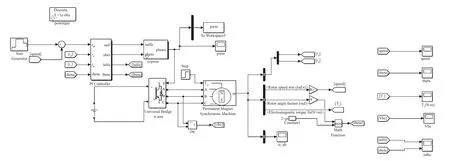
图3 SPMSM无位置速度传感器矢量控制仿真系统

主电路由输入直流DC经过三相逆变后驱动永磁同步电机。电机的额定功率P=1.5 kW，额定电压V=380 V，极对数为2，定子电阻Rs=0.35 Ω，定子d轴的电感Ld=5.2 mH，定子q轴的电感Lq=11.9 mH，磁链ψ=0.113 493 Wb，转动惯量J=0.004 06 kg·m2。将初始角频率、转子角度以及定子电流均设置为0，具体电机参数如表1所示，仿真设置如图4所示。

表1 SPMSM电机参数

图4 SPMSM仿真参数设置

系统利用状态空间矢量估算得到转速，在设定转速做差比较后，进行电流PI调节得到转矩调节器输出uq。对三相电流经Clark变换和Park变换后得到的Id与idref=0进行比较。电流PI调节器调节得到输出ud。uq与ud作为电压调节器的输入，与估算得到的角度θest，经Park逆变换后得到两相静止坐标系下电压ualfa和ubeta，具体实现框图如图5所示。

系统采样离散仿真时，开关器件开关频率设为10 kHz，死区时间设为2 μs，具体设置如图6所示。

图5 实现框图

图6 矢量控制开关频率及离散时间设置

3 系统仿真

SVPWM发生模块是实现矢量控制的关键模块，将来自两相静止坐标系下的电压ualfa和ubeta作为输入。与三角载波相比较的输入信号，输出的调制波与三角载波比较延迟后，得出6路SVPWM波形。SVPWM具体实现框图如图7所示[5]。

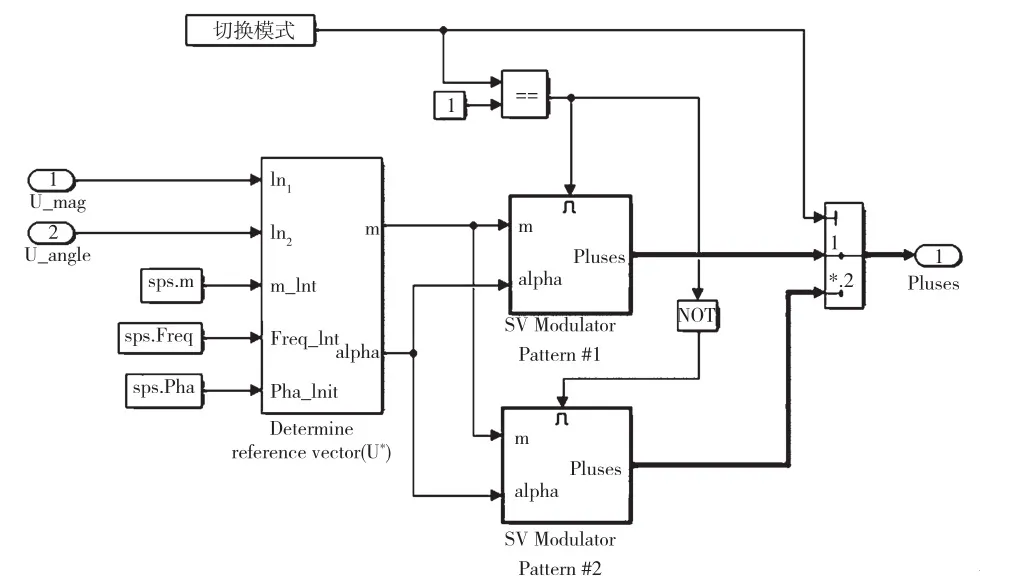
图7 SVPWM控制关键算法模块

设置完成模块的上述参数后，设置终止仿真时间为5 s。系统在带5 N·m满载下启动，在0.1 s时突卸载至半载3 N·m。同时，设置Stair Generator模块频率在0～0.4 s时在100 r/m，0.4 s时升频至300 r/m，0.6 s时继续升频至1 200 r/m，1.6 s时降至600 r/m，而在4 s时又降至300 r/m。不同时间加载及升降频如图8所示。

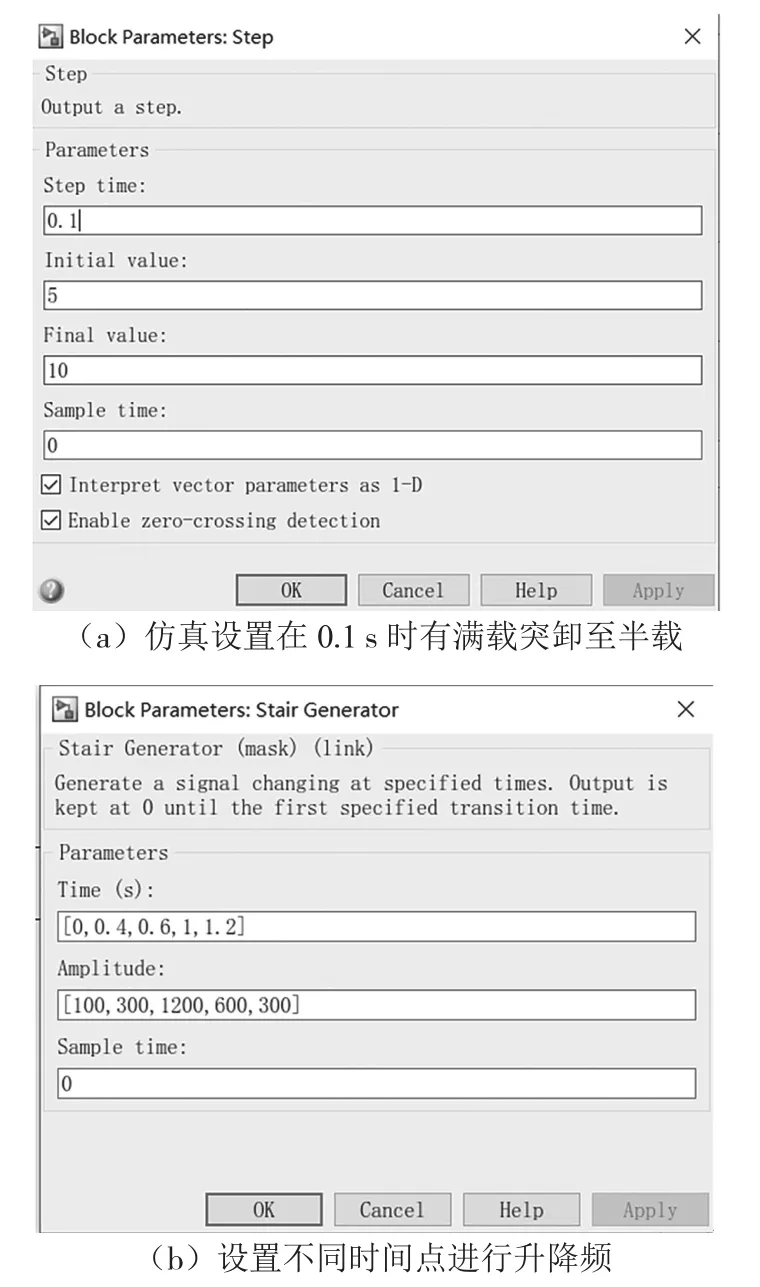
图8 设定不同时间点进行卸载及升降频

仿真得到的电机各关键参数波形，如图9所示。

从仿真结果可以得出，定子电流在重载10 N·m、低速100 r/m重载启动时，三相定子电流波形无畸变，启动电流及转矩均在10 A及10 N·m以内，在0.4 s及0.6 s时刻升频至300 r/m及1 200 r/m时转速短暂稍有上升，但在100 ms内又快速回到设定值，此时对应转矩也短暂抖动，但基本在50 ms内快速回到设定值，在1.0 s及1.2 s突然降频时又快速回归至设定值，对应转速及转矩抖动小。从波形可以看出，基本在80 ms内又回到设定值，对应电机定子电流稍有抖动，但都在可控电流范围内，无过冲和过流情况发生，转子实际角度切换平稳，系统运行正常，充分验证了提出的SPMSM低速下无位置速度传感器矢量状态观测器控制算法的可靠性与可行性。

4 结 论

在Matlab/SiMulink上搭建SPMSM无位置低速矢量控制系统模型进行仿真，验证电机运行平稳，启动过程中电流无冲击，电机转矩波动小，能适应低速重载下启动，可实现在最低转速300 r/m的情况下正常运行。

图9 电机定子电流、转速、转子角度及电磁转矩波形