硼、铝和镓掺杂对硅纳米管电子结构和光电性质的影响

秦成龙 罗祥燕 谢 泉

(贵州大学大数据与信息工程学院，新型光电子材料与技术研究所，贵阳 550025)

0 引言

随着碳纳米管的发现以及单壁碳纳米管的成功合成[1-3]，越来越多的研究者致力于纳米管的研究。硅作为碳在周期表中同一族的元素，有着与碳相似的性质，因此硅纳米管(SiNTs)成为新一代纳米管的有力候选材料之一。SiNTs可以通过单层的蜂窝状纸片(类似于石墨烯)卷曲而成，它的结构同样可以通过手性参数表示，根据手性参数的不同也可以分为锯齿型(n，0)、扶手椅型(n，n)和手性型(n，m)。大量研究表明，碳纳米管倾向于sp2杂化从而能够稳定地存在，而SiNTs更倾向于形成金刚石型的sp3杂化，且SiNTs的键长相对于碳纳米管更长，这就导致了π键的重叠度较低，进一步降低了SiNTs的稳定性[4-6]。为了提高单壁SiNTs的稳定性，研究者用氢、氧、过渡金属元素掺杂提升了SiNTs的稳定性[5-11]。以上研究表明掺杂不仅提高了SiNTs的稳定性，同时也可以改变它的电子结构以及光学性质。

对于本征SiNTs，大量研究表明其不够稳定，在电子特性方面有着类似于碳纳米管的手性规律[17-21]。在SiNTs掺杂方面，Yu等[13]发现，经过P掺杂单壁扶手型SiNTs的能带结构从间接带隙变为直接带隙，禁带宽度变窄，导电性增强，为SiNTs在光电器件方面的应用提供了理论基础。He等[6]通过自旋极化密度泛函研究了Co掺杂的单壁SiNTs，研究表明Co原子的掺杂不仅有效地提高了纳米管的稳定性，并且在一定程度上提高了纳米管的导电性，为纳米设备的设计提供了理论基础。此外铝[15]、碳和锗[16]的掺杂也有研究。Durgun等[5]研究了过渡金属掺杂小直径SiNTs的稳定性和电子特性，发现原本不稳定的SiNTs在加入过渡金属后能够稳定地存在，并且获得了一些强磁性。

硅是Ⅳ族元素，而Ⅲ族元素是硅在周期表中的临近主族元素，这就决定了它们的化学性质更加接近，在掺杂的时候更能形成稳定的结构。Ⅲ和Ⅴ族的混合纳米管[5]也成了当下研究热点，例如BN纳米管、GaN纳米管和AlN纳米管。研究表明Ⅲ和Ⅴ族的混合纳米管相比于SiNTs有着更好的稳定性以及新的电子特性。我们针对Ⅲ族元素B、Al、Ga掺杂(相应的 SiNT 为 SiNT-B、SiNT-Al、SiNT-Ga)对于SiNTs的稳定性以及电子特性的影响进行了研究。

1 结构模型与计算方法

1.1 结构模型

在选择模型前，计算了n=10～16的锯齿型SiNTs(n，0)的电子特性，发现带隙在n=14打开，这与Durgun等[5]计算的n=12略有差异，这是由于选择的GGA(广义梯度近似)泛函往往会低估带隙[14,27]，但这并不影响掺杂前后的对比。为了更好地比较掺杂前后的带隙变化，并控制计算原子的数量，我们选取了(14，0)的锯齿型SiNTs作为研究对象。采用周期性边界条件，在a×b×c的三斜超胞中进行理论计算。如图1所示，其中SiNTs的轴向沿超胞c的方向无限延伸。掺杂的SiNTs选取的是1×1×2的超胞，共112个原子，并在其中心位置进行Ⅲ族元素的替位掺杂，掺杂率为0.89%。

图1 单壁锯齿型(14,0)SiNTs的结构图Fig.1 Structure of single-wall zigzag(14,0)SiNTs

1.2 计算方法

我们最初建立的结构往往是不稳定的，需要通过精密的结构优化计算寻找出其总能和应力最小的结构。因此在进行第一性原理计算之前，体系的结构优化是非常必要的。这里我们采取了BFGS算法对SiNTs进行了结构优化，其优化结束条件为每个原子的原子间自洽允许误差(SCF tolerance)等于1×10-6eV，最小应力为0.5 eV·nm-1。

采用密度泛函理论(DFT)的CASTEP模块，选择超软(ultrasoft)赝势平面波和GGA下的PBE泛函进行第一性原理计算。为了保证足够的精确性，采用1×1×19 Monkhorst-Pack形式的高对称特殊K点处理布里渊区的积分，每个原子的总能量自洽允许误差为1×10-6eV，平面波的截断能量为350 eV。为了防止临近纳米管的影响，在a、b晶格矢量方向间隔了1 nm的真空层。

2 结果与讨论

2.1 结构优化和稳定性

根据以前的SiNTs掺杂计算[13,15-16]结果，其结构优化前后晶胞以及晶格参数变化并不大，鉴于本文计算体系规模较大，对晶胞以及晶格参数的影响更加微小。为了提升计算速度，设定优化前后晶格常数和体积不变：晶格常数a=b=3.045 nm，c=1.33 nm，晶胞体积V=10.677 4 nm3。如图2所示，优化后的本征SiNTs及其掺杂体系在结构上有了很大的变化，其结构不再是碳纳米管的光滑管状结构，而是形成了管壁原子凸起的褶皱型管状结构。从图3的局部轮廓图来看，凸起的原子及其相连的3个原子形成了一种类似于金刚石的sp3杂化结构，整个纳米管既有这种褶皱的结构，也保留了其最初的光滑结构。图3b和3c为本征SiNTs结构优化后的局部轮廓图，其键角分布是完全不同的。进一步引入键角和∑α=α1+α2+α3，∑α为X原子(X=Si、B、Al、Ga)与相邻原子 Sia、Sib、Sic的键角和，并且理想sp3杂化(金刚石结构)的 ∑α=3×109.47°=328.4°，理想的sp2杂化(石墨烯)的 ∑α=3×120°=360°。从表1中可以看到，图3b中的∑α=337.022°，更加接近于sp3杂化；图3c中的∑α=358.677°，与sp2杂化非常接近。由此我们可以推断，结构优化后的SiNTs的内部结构由sp2和sp3杂化共同构成，是一种表面褶皱的管状结构，这与之前的研究一致[5-6,20-21,24]。实验上也证实了SiNTs最为可能的结构便是这种褶皱型的管状结构，并且由sp2杂化和sp3杂化共同构成[25-26]。

图2 结构优化后的本征(a)、B掺杂(b)、Al掺杂(c)和Ga掺杂(d)SiNTsFig.2 Intrinsic(a),B-doped(b),Al-doped(c)and Ga-doped(d)SiNTs with optimized structure

图3 本征SiNTs及其掺杂体系的局部轮廓图:(a)本征SiNTs优化前;(b、c)本征SiNTs优化后;(d)B掺杂;(e)Al掺杂;(f)Ga掺杂Fig.3 Partial outline view of an intrinsic silicon nanotube and its doping system:(a)intrinsic silicon nanotube;(b,c)optimized intrinsic SiNTs;(d)B-doped;(e)Al-doped;(f)Ga-doped

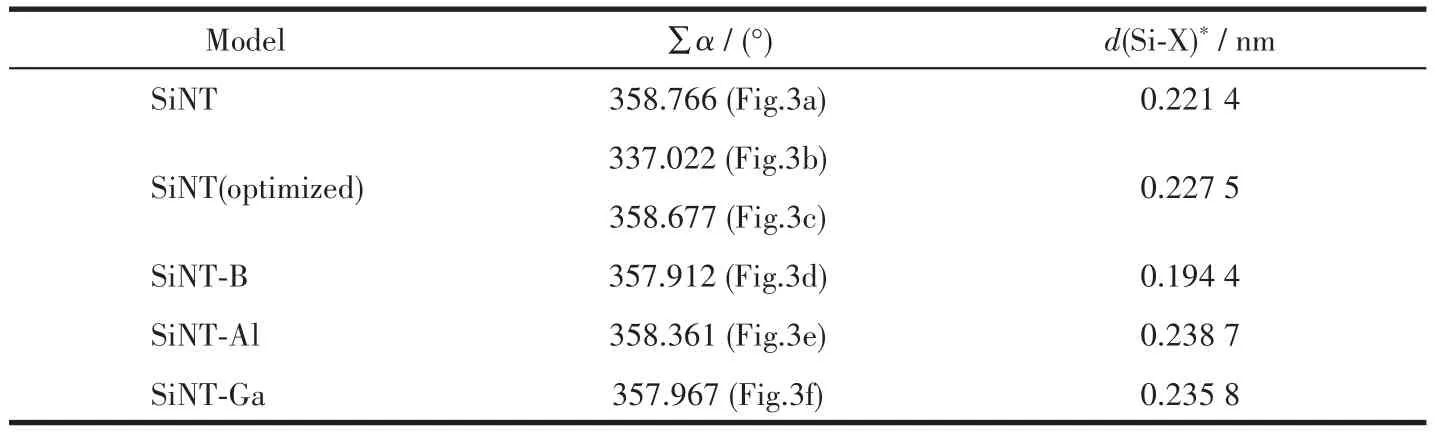
表1 本征SiNTs及其掺杂体系的键角和键长Table 1 Bond angles and lengths of intrinsic SiNTs and its doping systems

从表1可知，优化后的本征SiNTs键长有所增大，与 He 等[6]计算的(8，0)锯齿型 SiNTs(0.228 nm)、Zhang[15]以及 Yu[16]计算的扶手椅型(6，6)SiNTs(0.228 nm)基本一致。Al掺杂SiNTs的Si-Al键长为0.238 7 nm，略微大于Zhang[15]所计算的0.231 nm。根据量子化学理论[16]，铝、镓的离子半径比硅的离子半径略大，硼的离子半径略小于硅，按理掺杂原子与硅原子的键长会随着离子半径的大小而变化，这与图3以及表1所标示的一致。从图3中的键角来看，无论是本征SiNTs还是其掺杂体系，左下方与右下方(d1≈d2)的键角更为接近，说明了Sia-X和Sic-X(X=Si、B、Al、Ga)在化学性质上更为接近。SiNTs掺杂体系的∑α更加接近于360°，说明掺杂原子与邻近硅原子形成了sp2杂化。

为了分析Ⅲ族元素掺杂单壁锯齿型(14，0)SiNTs的稳定性，计算了B、Al、Ga掺杂单壁锯齿形型(14，0)SiNTs体系的形成能Ef。定义掺杂SiNTs体系的形成能Ef为

其中，ESiNT-X为Ⅲ族元素(X=B、Al、Ga)掺杂单壁锯齿(14，0)SiNTs体系的总能量；ESiNT为本征单壁锯齿型(14，0)SiNTs体系的总能量，EX和ESi分别为Ⅲ族元素(B、Al、Ga)和Si原子的化学势。此式表明形成能越小其体系越稳定。

如图 4所示，B、Al、Ga掺杂单壁锯齿型(14，0)SiNTs的形成能均为负值，表明掺杂SiNTs均放出了能量，由此可知B、Al、Ga掺杂SiNTs能够有效地提高 SiNTs的稳定性。从形成能的大小来看，Ef，B＜Ef，Al＜Ef，Ga，B掺杂纳米管放出的能量最高，其次为Al，最后为Ga。从图中也可以明显看到当Ⅲ族元素在周期表中从上到下掺杂SiNTs时，形成能不断增大，其相对稳定性不断降低。由此我们可以推论，随着掺杂元素原子序数的不断增大，其形成能不断增大，其形成的掺杂体系稳定性不断降低，但总的来说B、Al、Ga掺杂对SiNTs的稳定性都有着一定的提升。

图4 B、Al和Ga掺杂单壁锯齿型(14,0)SiNTs的形成能Fig.4 Formation energy of single-wall zigzag(14,0)silicon nanotube doped by B,Al and Ga

2.2 电子结构特性

如图5所示，我们给出了本征单壁锯齿型(14，0)SiNTs掺杂前后的能带图。从图5a可知，本征SiNTs的价带顶和导带底几乎交叠在费米能级处，但这里并未完全交叠，其带隙为0.01 eV。因为其禁带宽度很小，只需要获得极少的能量便可以跃迁到导带从而导电，可以认为是金属性质。从图5b～5d可以明显看到，相对于本征SiNTs，经过掺杂后的SiNTs，导带底均有着往高能区上升的趋势，而价带顶保持在费米能级附近，促使了(14，0)SiNTs的带隙增大，实现了SiNTs从金属性向半导体性质的转变。从Ga掺杂的纳米管能带图(图5d)中可以明显看到在价带底部(-14.6 eV)出现了杂质能级。B、Al、Ga掺杂本征(14，0)SiNTs的带隙大小随着原子序数的增加不断减小，依次为 0.191、0.158、0.149 eV。Zhang[15]计算了Al掺杂(6，6)扶手椅型SiNTs，其带隙从 0.42 eV降到了0.02 eV，出现了从半导体到金属的转变，这与我们计算的完全相反。由此可以发现，即使相同的掺杂元素，对于不同手性的SiNTs的电子结构特性影响也完全不同。也有文献报道了C、Ge对于(6，6)扶手椅型SiNTs的掺杂[16]，尽管C、Ge同为Ⅳ族元素，其对纳米管的电子特性影响却不相同，通过C掺杂，可使SiNTs的禁带宽度减小，而Ge掺杂可使SiNTs的禁带宽度增大。然而本文计算的Ⅲ族元素B、Al、Ga对于SiNTs的电子特性影响却是一致的。

图5 本征(a)、B掺杂(b)、Al掺杂(c)和Ga掺杂(d)单壁锯齿型(14,0)SiNTs的能带图Fig.5 Band structures of intrinsic(a),B-doped(b),Al-doped(c)and Ga-doped(d)zigzag(14,0)SiNTs

表2 SiNTs掺杂前后TDOS贡献分布表Table 2 Distribution of TDOS contribution for SiNTs before and after doping

从表2可知，在导带底，Si3p、Si3s对本征SiNTs及其掺杂体系的总态密度均参与了贡献，并且掺杂体系的总态密度还取决于掺杂原子的s态电子和p态电子。通过对图6的对比发现，在贡献程度上B、Al的s态电子比p态电子贡献更大，而Ga的p态电子贡献略多于s态电子。在价带顶，Si3p均参与了本征及其掺杂体系总态密度的贡献，此外，掺杂元素的p态电子对各自体系总态密度也有贡献。在价带底，Si3p、Si3s均参与了对本征SiNTs及其掺杂体系的总态密度贡献，掺杂体系总态密度还取决于其掺杂元素的s态电子，唯一不同的是SiNT-B还由少量的B2p构成。从图6还可以明显看到，SiNT-Ga的总态密度在-15.5～13.5 eV出现了杂质态，其完全由Ga3d态电子贡献。

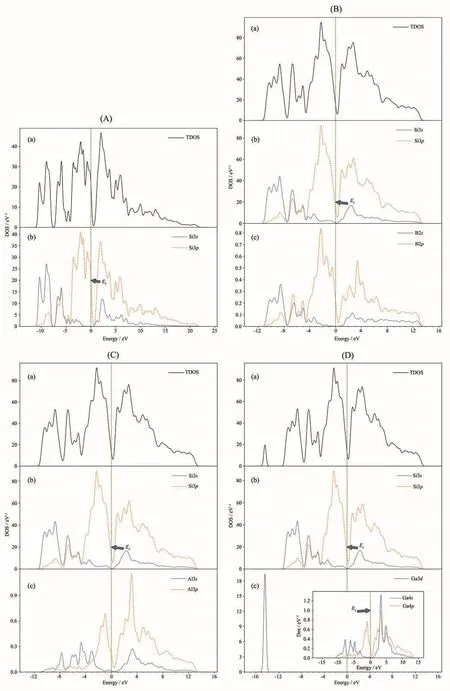
图6 本征(A)、B掺杂(B)、Al掺杂(C)和Ga掺杂(D)SiNTs的总态密度图和分态密度图Fig.6 TDOS and PDOS of intrinsic(A),B-doped(B),Al-doped(C)and Ga-doped(D)SiNTs

B、Al、Ga替代硅的掺杂属于非等电荷掺杂，会产生多余的空穴参与导电，空穴浓度高于自由电子的浓度，其掺杂可以认为是一种P型掺杂。相对于Si元素而言，Ⅲ族元素B、Al、Ga没有多余的p态电子，虽然并没有像N型掺杂[13]那样在费米能级附近形成施主杂质能级，但由于Ga3d态电子的贡献，SiNT-Ga产生了杂质能级，与图5d的能带图一致。由于其远离费米能级，又被称为深能级杂质，对于整个体系的带隙以及导电性并没有影响。在导带区域，Si3p态电子、Si3s态电子、X3p态电子以及少量的X3s态电子(X=B、Al、Ga)相互作用，驱动导带底的电子向高能区偏移，而价带顶的电子位置基本不变，从而形成图5所示的B、Al、Ga掺杂单壁锯齿型(14，0)SiNTs最小禁带宽度变宽的现象。

2.3 介电函数与光吸收特性

单壁锯齿型(14，0)SiNTs的光学性质取决于它的电子结构，可以由介电函数以及与之相关的反射系数和吸收系数等来表征。光在介质中传播，当需要考虑吸收的影响时，介电函数ε(ω)[13,22]需要用复数来表示，为此引入以下公式：

图7～9分别给出了B、Al、Ga掺杂前后单壁锯齿型(14，0)SiNTs的复介电函数实部图、虚部图以及吸收光谱图。从复介电函数实部图(图7)可看出本征SiNTs的静态介电函数为4.49，其复介电函数实部在0.85 eV左右出现一个最大介电峰，随着能量的增加，在3.35 eV左右出现一个局域最大介电峰，并且实部介电峰在10 eV后逐渐趋于平稳。从图中可知B、Al、Ga掺杂的SiNTs的复介电函数实部几乎重合在一条线上，对SiNTs的光学性质表现出了强烈的一致性，其原因是B、Al、Ga的核外价电子都是s和p态电子且核外价电子数目相同，在化学性质方面有着很大的相似性。同时随着B、Al、Ga杂质的引入，SiNTs的静态介电常数分别变为6.94、6.96、7.02，相对于本征SiNTs，B、Al、Ga掺杂SiNTs的静态介电常数有所增大。半导体材料的介电关系[23]为：ε(0)≈1+(hw'/Eg)2，其中w'为等离子频率，Eg为半导体的禁带宽度。随着Ga、Al、B掺杂SiNTs静态介电函数不断地增加(εB(0)＜εAl(0)＜εGa(0)),其掺杂SiNTs的禁带宽度依次减小(Eg,B＞Eg,Al＞Eg,Ga)，这一现象与图5的能带图完全吻合。

图7 掺杂前后(14,0)SiNTs的复介电函数实部Fig.7 Real part of complex dielectric function of(14,0)SiNTs before and after doping

图8为B、Al、Ga掺杂前后(14，0)SiNTs的复介电函数虚部图，本征SiNTs在1.55 eV附近出现了一个较大的吸收峰，随着能量的增大，在4.05 eV出现了一个尖锐的最大介电吸收峰。从图中可知，B、Al、Ga掺SiNTs的复介电函数虚部走势在图中几乎重合为一条线，其原因与上面提到的一致。同时随着B、Al、Ga杂质的引入，掺杂SiNTs的2个吸收峰峰值明显增大，相应的带宽也有所宽化，掺杂SiNTs的2个吸收峰向低能区方向略微偏移，从而出现了介电峰红移的现象。

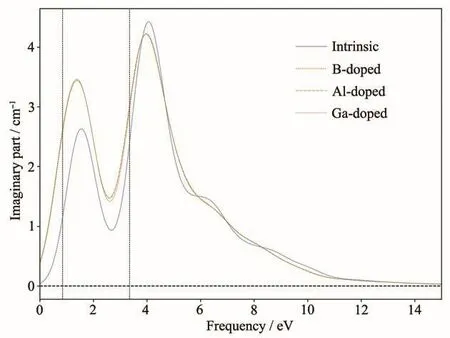
图8 掺杂前后(14,0)SiNTs的复介电函数虚部Fig.8 Imaginary part of complex dielectric function of(14,0)SiNTs before and after doping

图9给出了B、Al、Ga掺杂前后单壁锯齿型(14，0)SiNTs的吸收光谱图。本征SiNTs的吸收光谱在1～3.26 eV的红外和可见光波段出现较强烈的光吸收峰，其光吸收系数均在1×104以上；3.26～12.4 eV的紫外光波段出现非常强烈的光吸收峰，其平均光吸收系数均在5×104以上。这表明单壁锯齿型(14，0)SiNTs对于紫外光有着很强的吸收特性，并且对于红外和可见光波段也有着良好的吸收特性，可以作为紫外光探测器和太阳能电池的优良材料。B、Al、Ga掺杂SiNTs的吸收系数走势依旧重合为一条线。掺杂的SiNTs在红外和可见光波段吸收带宽有所增加，且峰值明显增大，表明引入B、Al、Ga杂质能够有效提高SiNTs的红外和可见光吸收特性；在紫外光波段，其吸收系数有增有减，总体保持了本征(14，0)SiNTs的高吸收特性。

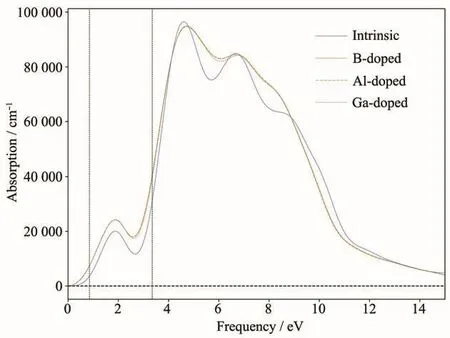
图9 掺杂前后(14,0)SiNTs的吸收光谱Fig.9 Absorption spectra of(14,0)SiNTs before and after doping

3 结 论

利用基于密度泛函理论的第一性原理的方法，计算了本征单壁锯齿型(14，0)SiNTs及其B、Al、Ga掺杂体系的形成能、能带结构、态密度和光学性质，结果表明：

(1)SiNTs的管状结构更加倾向于sp3杂化，其稳定结构为sp2和sp3杂化共同构成的褶皱型纳米管结构。

(2)通过对B、Al、Ga掺杂本征单壁锯齿型(14，0)SiNTs形成能的对比，我们发现B、Al、Ga掺杂均可以提高SiNTs的稳定性，随着掺杂元素原子序数的增大，其掺杂体系的稳定性不断降低，稳定性由强到弱依次为SiNT-B、SiNT-Al、SiNT-Ga、SiNT。

(3)本征单壁锯齿型(14，0)SiNTs是一种窄带隙材料，其带隙为0.01 eV，可以认为具有金属性质；同时随着B、Al、Ga杂质的引入，SiNTs的带隙变宽，实现了SiNTs从金属性向半导体性质的转变，并且带隙随着掺杂元素原子序数的增大而减小。

(4)B、Al、Ga在周期表中同为第Ⅲ族元素，有着非常相似的化学性质。我们发现它们的介电函数的实部和虚部以及吸收系数在图中几乎重合在一起，表明了B、Al、Ga掺杂对单壁锯齿型(14，0)SiNTs的光学性质有着完全相同的影响。B、Al、Ga掺杂单壁锯齿型(14，0)SiNTs对于紫外光有着很强的吸收特性，并且对于红外和可见光吸收有着明显的提升，可以作为紫外光探测器和太阳能电池的优良材料。