载体初始姿态对单轴旋转惯导误差传播的影响*

2020-11-11徐志浩周召发徐梓皓常振军

弹箭与制导学报 2020年3期

关键词：惯导单轴系统误差

徐志浩，周召发，郭琦，徐梓皓，常振军

(1 火箭军工程大学兵器发射理论与技术国家重点学科实验室，西安 710025； 2 96902部队，北京 100000)

0 引言

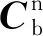
1 单轴旋转惯导系统误差方程

1.1 姿态误差方程

旋转调制型捷联惯导系统姿态误差方程为：

(1)

(2)

式中：s系为IMU坐标系，εs、δKg、δG分别为陀螺常值漂移、标度因数误差矩阵和安装误差矩阵。

1.2 速度误差方程

旋转调制型捷联惯导系统速度误差方程为：

(3)

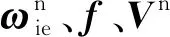
(4)

式中：▽s、δKa和δA分别为加速度计零偏、标度因数误差矩阵和安装误差矩阵。

1.3 位置误差方程

(5)

式中：VE、VN、VU分别为载体在导航系下东北天方向速度，δVE、δVN、δVU分别为载体在导航系下东北天方向速度误差，L、λ、h分别为载体所在点的纬度、经度和高程，RM、RN分别为子午圈和卯酉圈的曲率半径。

2 旋转调制的自补偿原理

2.1 静基座条件下的系统误差传播方程

因为纯惯导解算的高度通道是发散的，故在分析系统误差特征方程时不考虑δVU和δh。根据式(1)、式(3)和式(5)得，静基座条件下的系统误差方程为[8]：

(6)

由式(6)可知，由于经度误差δλ并没有以输入量的形式出现在其他系统误差方程中，即经度误差在系统回路之外，对系统的动态特性不产生影响，故在建立误差特征方程时暂不考虑δλ。

忽略经度误差δλ后，将式(6)的前6个方程改写为矩阵形式：

(7)

为了便于分析，下面将地球近似为球体并忽略高程h，即设RM=RN=R。将式(7)简记为：

(8)

对式(8)进行拉普拉斯变换，得到静基座条件下的误差传播方程为：

(9)

式中：N(s)为系统特征矩阵(sI-F)的伴随矩阵；Δ(s)为系统特征方程。

(10)

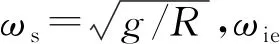
[s2+(ωs-ωiesinL)2]

(11)

求解式(11)，得系统的特征根为：

(12)

对式(9)作拉普拉斯反变换，可得到式(6)中前6个状态量的解析解，因经度误差δλ不在式(7)中，需要单独计算。由式(6)可知:

(13)

对式(13)进行拉普拉斯变换得：

(14)

代入δVE(s)，作拉普拉斯反变换，即可得到经度误差δλ的解析解。

忽略解析表达式中的振荡项，保留常值项和积累项，可以得到惯性器件等效常值误差与系统误差的函数关系为：

(15)

2.2 陀螺常值漂移的自补偿原理

设初始时刻IMU坐标系与载体坐标系重合， IMU绕竖直方向以恒定的角速度ω开始转动，则t时刻IMU坐标系与导航坐标系关系为[9]:

(16)

仅考虑常值漂移时，由式(16)得:

(17)

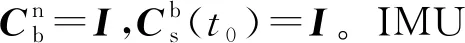
(18)

(19)

2.3 载体初始姿态对等效陀螺常值漂移的影响

当IMU以角速度ωc绕zs轴连续旋转时，直接对式(17)整周期积分得:

(20)

由于姿态矩阵是单位正交阵:

(21)

将式(21)代入式(20)得：

(22)

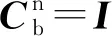
3 仿真试验与分析

为了直观反映旋转调制过程的自补偿效果，以单轴连续旋转方案为背景设计仿真试验。从式(6)系统误差模型出发，进行符号表达式的拉氏变换和反变换。而后，将参数值代入拉氏反变换后的公式，得到对应图像，以使得理论推导的解析表达式(15)与MATLAB符号运算的图像相互印证。

3.1 载体系与导航系重合时的误差传播仿真

图1 x,y轴陀螺漂移引起的导航误差对比图

如图1所示，未旋转调制时，陀螺常值漂移除了引起周期振荡传播的误差外，还产生航向角和纬度的常值误差，更严重的是产生随时间积累的经度误差。单轴连续旋转将与旋转轴垂直平面内的陀螺常值漂移调制成周期变化的量，经过积分后在水平面内的作用结果为零，使导航误差明显减小。仿真结果与理论分析一致。

(23)

(24)

3.2 载体系与导航系任意姿态时的误差传播仿真

如图2所示，当横滚角γ=0°且俯仰角θ=0°时，航向角ψ的取值对zs轴陀螺漂移引起的导航误差没有影响，与前述理论分析一致。

将θ=10°,γ=10°,ψ=270°代入式(22)得:

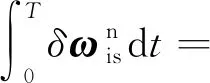
(25)

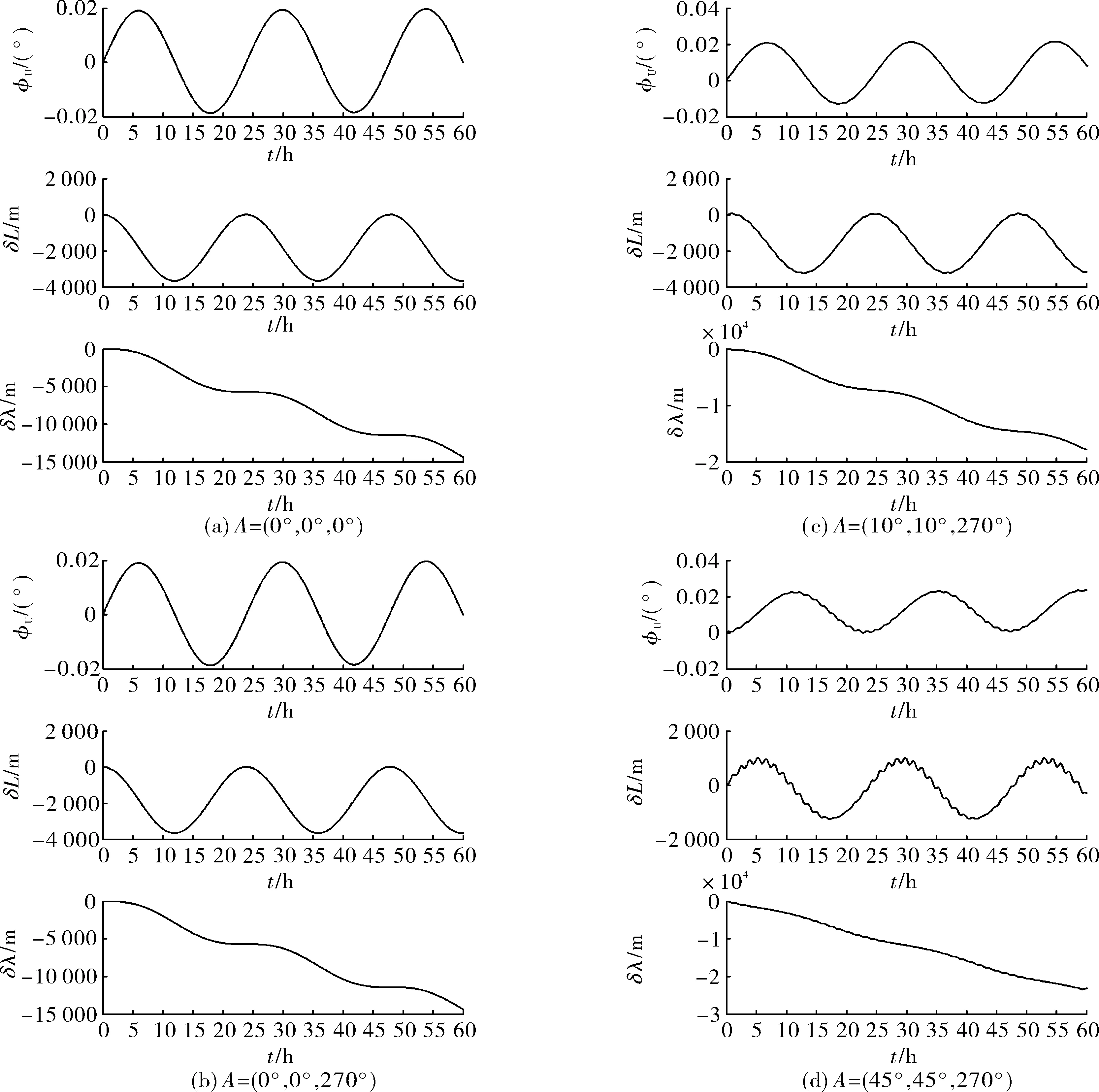
图2 不同初始姿态时z轴陀螺漂移引起的导航误差对比

将θ=45°,γ=45°,ψ=270°代入式(22)得:

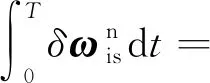
(26)

对比式(25)和式(26)，与图2(c)相比，图2(d)δωN较大，引起式(15)中与δωN相关的航向失准角φU的常值项增大，故图2(d)φU的曲线均值略大于图2(c)φU。由于θ=45°,γ=45°,ψ=270°时δωN较大且δωU较小，代入式(15)中可得纬度误差δL的常值项数值增大，因此图2(d)δL的曲线均值较图2(c)明显上移。

因此，相同时间内图2(d)δλ的积累项误差大于图2(c)。仿真结果与理论分析一致。

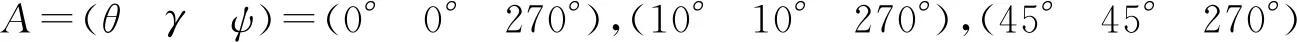
根据式(15)可知影响航向角精度的主要因素是δωE。对于实际的单轴旋转惯导系统，绝大多数的初始对准环境为ψ≠0。虽然使δωE=0的θ、γ组合有多种，但在ψ的真值未知或存在误差时，θ、γ除(0,0)外的其他解不能准确求出。为了实现旋转调制效果的最优且简化操作流程，应将载体调至水平即θ=0,γ=0，只需要一个水准器即可。室外进行车载初始对准时，若难以准确调平，也应尽量选择较平整的地势。