圆锥运动下几种姿态算法的比较与误差建模*

熊丽娟，朱洪涛，王志勇，曹娟华，周 波

(1 南昌大学机电工程学院， 南昌 330031； 2 南昌航空大学航空制造工程学院， 南昌 330063；3 南昌航空大学测试与光电工程学院， 南昌 330063)

0 引言

实时姿态解算是导航、机器人、远程操作和虚拟现实等工程领域的重要技术之一[1-4]。计算机和传感器的飞速发展对姿态精度和计算速度提出了更高的要求。此两者不仅和传感器性能有关，还和处理器所采用的姿态算法紧密相关。评判选择姿态算法时，常须考虑其在最不利条件下的性能。圆锥运动因可能引起最大不可交换误差[5-6]，被众多文献认定为最不利条件。但常用姿态算法在不同圆锥运动条件下的性能表现尚未得到系统研究。

姿态解算方法中，四元数法因其非奇异性、简单性和计算时间短等优点而成为目前最流行的方法[7-9]。 文中针对4种基于四元数的常用高精度姿态算法，研究它们在不同圆锥运动条件下的姿态解算性能。这4种算法分别为：四子样旋转矢量算法(RV4)，四阶龙格库塔算法(RK4)，四阶泰勒算法(T4)和五阶泰勒算法(T5)。为进行较全面的分析，文中通过变化锥进步长和锥半角进行了一系列圆锥运动仿真实验。实验以姿态角误差，即偏航、俯仰和横滚角3者的误差作为结果输出，籍此研究4种算法的姿态解算精度，并归纳建立4者的姿态角误差模型。相较而言，前人文献更倾向于依据误差漂移参数[1]、旋转矢量幅值误差或姿态四元数误差[5, 7, 10]来评价姿态算法的精度。这类误差模型因推算过程有假设与简化存在，并不准确，亦不利于理解和用作误差补偿。

所选4种算法虽非当前精度最高的姿态算法[11-13]，但因文中意在展示一种新的姿态算法研究方式，故并不需要遍历各种高级算法。另，因篇幅有限，文中仅展示了实验结果中有代表性的一部分。

1 姿态解算数学模型

姿态解算需先更新姿态四元数，再将其换算为姿态角，即横滚角、俯仰角和偏航角。除旋转矢量法外，姿态四元数的更新一般以式(1)为基础：

(1)

(2)

(3)

θ=-arcsinc31

(4)

式(4)中atan2是C++中的函数，返回-π ～ π范围的弧角。当θ= ±π/2时，由于横滚轴和偏航轴已成平行轴[1]，故无法获取φ和ψ的唯一解。因此，当θ接近±π/2时，可采取交替更新φ和ψ的方法[1]。

2 圆锥运动下的四元数更新算法

图1 典型圆锥运动示意图

典型圆锥运动是因系统两个正交轴上同时被施以相位差90°的角振动而产生[1]，具体如图1所示：O-XYZ为导航坐标系，O-xbybzb为载体坐标系；OL是从导航到载体坐标系的旋转矢量，正在YOZ平面内以恒角速度ω0旋转，载体坐标系此时即作典型圆锥运动，其xb轴可看作在导航坐标系空间中一锥半角为α的圆锥面上滚动，OL幅值亦为α。将OL记为Φ：

(5)

式中：t为载体圆锥运动时间；文中仿真的载体零点状态如图1所示。Φ的等效姿态四元数为：

(6)

载体相对导航坐标系的角速度为：

(7)

根据式(6)，不同时刻的精确姿态角可以算得；而式(7)可作为角速度传感器测得的转速，实现圆锥运动仿真。

2.1 RV4算法

在姿态更新区间Δt内，载体从(k-1)Δt到kΔt时刻的四子样旋转矢量μk计算如式(8)[7]。

(8)

式中：k=1,2,3,…；μk1、μk2、μk3、μk4分别对应四分之一更新区间内的角积分。对典型圆锥运动而言，μki(i=1，2，3，4)可通过对式(7)积分得到。

求出对应旋转矢量μk的四元数为：

(9)

式中：μk为μk的幅值。

(10)

2.2 RK4算法

典型圆锥运动下，姿态四元数传播方程具体化为：

(11)

qk=qk-1+(K1+2K2+2K3+K4)Δt/6

(12)

式中：K1、K2、K3、K4按式(13)顺序求解：

(13)

2.3 泰勒级数算法

使用泰勒级数法[14]求解方程(11)得：

(14)

式中：上标(j)代表求导阶数，l为所使用泰勒级数法的阶数。

3 实验结果

3.1 基础分析

文中变化锥进步长(即ω0Δt，简记为β)和锥半角α进行了一系列圆锥运动仿真实验。为方便起见，文中所有仿真中ω0均保持在30°/s，而Δt在0.1 ～ 4 s间变化，这样锥进步长β在3°～ 120°间变化；锥半角α在5°～ 85°间变化。

当α=5°、β=3°时，4种算法的姿态角误差如图2所示。此时4者精度由高到低排序为：RV4、T5、RK4、T4。图2还显示，由于圆锥运动中姿态角的周期变化，所有姿态角误差都以类谐波的形式随时间波动。

图2中120 s的仿真误差发展趋势不够明朗，因此仿真时长被延至20 000 s，其实验结果(未图示)清楚表明各算法的姿态角误差绝对峰值几乎均随时间线性增加，且横滚角误差发散速度基本都比偏航和俯仰角误差发散速度快。这与文献中所述“圆锥误差(漂

图2 120 s仿真中的姿态角误差(α=5°、ω0=30°/s、Δt=0.1 s)

移)主要出现在锥进轴上”[7, 15-16]相吻合。虽然多数文献根据其简化误差模型认为偏航和俯仰角误差基本无漂移[7, 15-16]，但仿真实验结果证明，这两者的绝对峰值其实也在累加(漂移)，只是速度通常没有横滚角误差发散得快。

3.2 误差建模

为研究姿态误差会如何随步长或其它因素的变化而变化问题，文中将4种算法在120 s仿真时间内的最大姿态误差，即最大姿态角绝对误差E绘于图3、图4之中。图3描绘了E在不同锥进步长下如何随锥半角α的变化而变化，图4则描绘E在不同锥半角下如何随锥进步长β的变化而变化。

图3 120 s仿真中最大姿态误差与锥半角的关系

图3、图4均反映出RV4、T5、RK4和T4这4者的精度排序并不总是不变的,比如，T4算法虽不如RV4和RK4精确，但并非总是不如T5；T5算法在锥进步长较小时精度较高，但随着锥进步长增大，其精度相比其余3者急速下降——也就是说，T5的精度易受步长影响；而最易受锥半角变化影响的是RV4算法，某些时候它的精度还不如RK4。

图4 120 s仿真中最大姿态误差与锥进步长的关系

由图3可知，当α不超过30°时，lgE与lgα间基本呈线性关系。由图4可知，当β不超过30°时，lgE与lgβ间亦基本呈线性关系。为此，可用式(15)表达4种算法的E与α、β之间的关系。

E=Aαmβn

(15)

式中：上标m即图3数据拟合线斜率，上标n即图4数据拟合线斜率，系数A取决于运动时长t和锥进速度ω0。对不同的算法，这3个参数自然不同。

根据上一小节中的分析，A值基本与时间t成正比，也与ω0成正比，故将式(15)中的A代以Cω0t，得：

E=Cω0tαmβn

(16)

式中:C是取决于算法的常数。

为确定4种算法的m和n值，将图3、图4中横坐标不超过30°的数据拟合直线，斜率m、n分别列于表1、表2中。

表1 不同锥进步长β下的m值

*使用部分数据拟合。

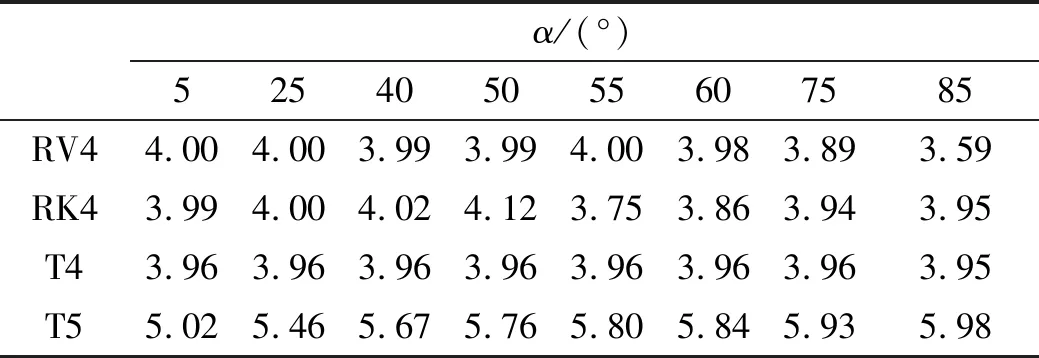
表2 不同锥半角α下的n值

表1显示：当β≤ 60°，RV4算法的m总在3左右；当β≥ 90°时，其m在4左右。深入剖析发现，β≤ 60°时，120 s仿真时间内RV4算法的最大姿态误差E为俯仰角误差；而β≥ 90°时，其E为横滚角误差。所以，m值从3跳变到4是因为E从俯仰角误差切换到了横滚角误差，或者说3是RV4俯仰角误差的m值，而4是RV4横滚角误差的m值。

须申明的是，当运动时间足够长，横滚角误差通常将成为3个姿态角误差中最大的，此时E即横滚角绝对误差极值。

表1还显示：①无论β如何变化，RK4和T4算法的m值均在2左右。因为在这两种算法的120 s仿真实验中，大多数情况E都是横滚角误差，所以其m值未出现跳变。②当β= 3°，T5算法的m在1左右；当β≥ 12°，其m在2左右。经剖析发现，1实为T5偏航角误差的m值，而2为其横滚角误差的m值。

同理由表2推知：①当α不超过75°，RV4横滚角误差的n总在4左右；②无论α如何变化，RK4横滚角误差的n总在4左右，T4横滚角误差的n亦在4左右，而T5横滚角误差的n总在6左右。

值得一提的是，表2中RK4算法的n值在α= 55°时突然降至3.75。这种突变在图3中也有出现——RK4的E值在α= 55°附近突然下降。图4则反映，当α从5°升至55°，RK4的精度从远不如RV4渐升至与其相当。经深入分析，这一现象源自RK4横滚角误差发散方向会随α增加而变化——当α升至一定值，其误差发散由朝正方向发展变为朝负方向发展。该转变点α值会随β值变化，β增大，转变点α值也渐渐增大；当β增至120°时，转变点消失(因为α不会超过90°)。横滚角误差发散方向的改变令RK4横滚角误差在转变点处大大减小并散失其误差支配地位。上述现象在4种算法中为RK4算法所独有，一定程度上提高了RK4算法对高机动运动环境的适应能力。这也是为什么一些学者会发现RV4的抗干扰能力不如RK4[17-18]。

综上，当α≤ 30° 且β≤ 30°时，圆锥运动t时长内以上4种算法的最大横滚角误差，记为|δφ|max，可建模如下：

(17)

式中：|δφ|max单位(°)，锥进速度ω0单位(°)/s，圆锥运动时长t单位s，锥半角α和锥进步长β单位(°)；利用实验结果算得系数C1、C2、C3、C4依次为：9.11e-19，2.63e-14，1.20e-13，5.31e-18。该式给出的是锥进轴姿态角误差模型，而非以往文献常给出的“圆锥误差模型[7]”(即文中旋转矢量μk的误差幅值模型)。

在同样使用环境下用4种算法分别进行1 200次姿态更新发现：RV4算法用时0.168 8 s， RK4算法用时0.270 7 s，T4算法用时448.049 6 s，T5算法用时1 365.3 s。显然，RV4是4者中计算速度最快的算法，而T5是四者中速度最慢的算法。

4 结论

文中研究了4种高精度姿态算法，通过分析其在圆锥运动下的姿态角计算误差，发现其精度排序将随条件的改变而变化。这和以往一些文献给出的精度优劣论断不一样[19-20]。

就计算速度而言，RV4和RK4算法比T4和T5算法快得多。综合考虑计算精度和速度，多数情况下RV4算法会是4者中姿态解算性能最佳者。

文中还建立了4种算法的锥进轴姿态角误差模型，亦即文中实验条件下的横滚角误差模型。在工程应用中，若能即时对待测物的角速度进行频域分析，可针对其包含的圆锥运动分量使用此误差模型进行误差预测乃至补偿[21-22]。