种养加销一体化生态循环农业模式中各主体合作演化博弈研究
2020-11-10高艳张凯淳
高艳 张凯淳


[摘要]种养加销一体化的生产模式能够良好地解决农业生产中生态和经济的发展矛盾,如何构建种养加销一体化的生产模式,提高产品质量和效益是亟待解决的问题。本文利用演化博弈模型对种养加销一体化生态循环农业模式各主体的合作决策行为进行分析,分析不同情况下的博弈行为,并进行数据仿真验证,得到各主体演化博弈的两种稳定结果,即各主体都不合作或都合作。当某一博弈主体因合作产生的成本大于收益时,会选择不合作的策略,博弈最终的均衡结果为都不合作。当博弈主体都能因合作获得额外的收益且多于运作成本时,博弈最终的均衡结果为都合作。
[关键词]种养加销一体化;演化博弈;演化稳定策略
[中图分类号]F321
[文献标识码]A
1 引言
当前的粮食消费和贸易对农业系统提出了更高的需求,生态环境面临着巨大压力,需要在粮食安全和环境影响之间作出权衡。而农民们往往在生产中投人大量的农药、化肥、地膜等要素以获得更大的经济效益,这引发了一系列生态环境问题,导致农业生产进入生态效益下降、经济效益无法提高的恶性循环,阻碍了农业的可持续发展。Anne-Kristin Lzes等指出通过循环利用和有效利用可再生资源,最大限度地减少废物和污染的产出,能够满足经济和生态的共同利益。Boone Lieselot等证明了与传统耕作方法相比,有機耕作在资源消耗方面具有明显的环境效益。Milutin Stojanovic认为,农业的生态修复和可持续发展需要从化学模式向生态设计模式转变。种养加销一体化“以养带种、以加促养、以销促加”的产业链结构,使农业与第二、第三产业相辅相成,构建了低能耗、低排放、高效率的产业化农业,形成了生态与经济的良性循环。我国地域广阔,发展出了如“水稻+”、 “猪一沼+”、林地复合等多种种养结合的生产模式。学者们从不同角度做了相关研究,例如詹国辉、张笑寒利用演化博弈方法分析影响合作的因素。屠文娟、柳键、陈莫凡等从农产品供应链视角运用演化博弈和数值仿真研究农户和合作社策略选择的影响因素,尤其是从构建绿色农产品供应链的角度分析政府、加工企业及农户的三方演化博弈分析,分析了不同驱动机制对供应链绿色化进程的影响。梁雯、李泉林、周业付和姜昊也采用动态博弈模型分析了不同农产品供应链合作模式下的利益关系及协调运作机制。
总之,对种养加结合生产模式的研究已较为成熟,但将产业链从生产延伸至销售的生产模式还需不断探索,因此,本文构建生产主体、加工主体、销售主体的三方演化博弈模型,求解不同决策下三方演化博弈的演化稳定策略,并进行数值仿真分析。
2 种养加销一体化生态循环农业模式各主体合作演化博弈模型构建
2.1 模型基本假设
(1)博弈主体。在种养加销一体化的产业链中,一共有三类参与主体,分别为生产主体、加工主体、销售主体。生产主体负责包括种植业和养殖业的农产品生产环节,加工主体负责农产品的加工与包装环节,销售主体负责农产品的推广与销售环节。
(2)信息不对称。博弈主体在互相作用下形成产业链,虽然形成一个完整的产业链,但三方所获取的信息并不完全对等,三方都仅具备有限信息。
(3)有限理性。博弈主体均为有限理性,在博弈过程中不断学习调整,最佳策略是需要在多次博弈的过程中得到的,即演化博弈的稳定均衡解不是一次性选择的结果。
(4)非对称博弈。博弈主体在动态的行为过程中具有差异,其特点体现在三方博弈收益矩阵是非对称的。
2.2 策略及参数的设定
(1)合作策略。博弈三方均采取两种策略: “合作”和“不合作”,“合作”代表博弈主体互相信任,进行信息共享,建立稳定的合作关系以达到共赢; “不合作”代表博弈主体没能进行信息共享,独自生产经营。
(2)生产主体的收益与支出。独自生产时的利润为R1,即总收入减去总成本。当与加工主体互相达成合作关系时,进行信息共享,此时生产成本会下降、收入会增加,利润增长为S1;当与销售主体互相达成合作关系时,进行信息共享,此时生产成本会下降、收入会增加,利润增长为Si。当生产主体选择“合作”策略时,会产生额外的运作成本C1。
(3)加工主体的收益与支出。由生产主体的收益与支出可知,加工主体独自生产时的利润为R2。当与生产主体互相达成合作关系时,利润增长为S2;当与销售主体互相达成合作关系时,利润增长为Si。当加工主体选择“合作”策略时,会产生额外的运作成本C2。
(4)销售主体的收益与支出。同理可知,销售主体独自生产时的利润为R3。当与生产主体互相达成合作关系时,利润增长为S3;当与加工主体互相达成合作关系时,利润增长为S3。当销售主体选择“合作”策略时,会产生额外的运作成本C3。
2.3 博弈收益矩阵构建
假设生产主体选择“合作”的决策概率为X,选择“不合作”的决策概率为1-X;加工主体选择“合作”的决策概率为Y,,选择“不合作”的决策概率为1-Y;销售主体选择“合作”的概率为Z,选择“不合作”的决策概率为1-Z。基于以上假设,可得到博弈过程中生产主体、加工主体、销售主体的三方收益矩阵,如表1所示。
3 各主体演化博弈均衡分析
3.1 博弈主体的期望收益与平均期望收益
生产主体采用“合作”策略时,获得的期望收益为EX,采用“不合作”策略时,获得的期望收益为E1-X,平均收益为,则其分别为:EX=YZ(R1+s1+Si-C1)+Y(1-Z)(R1+S1-C1)+(1-Y)Z(R1+Si-C1)+(1-Y)(1-Z)(R1-C1)E1-X=YZR1+Y(1-Z)R1+(1-Y)ZR1+(1-Y)(1-Z)R1
加工主体采用“合作”策略时,获得的期望收益为EEY,采用“不合作”策略时,获得的期望收益为E1-Y,平均收益为,则其分别为:EY=XZ(R2+S2+S2-C2)+X(1-Z)(R2+S2-C2)+(1-X)Z(R2+Si-C2)+(1-X)(1-Z)(R2-C2)EY=XZR2+X(1-Z)R2+(1-X)ZR2+(1-X)(1-Z)R2
销售主体采用“合作”策略时,获得的期望收益为EZ,采用“不合作”策略时,获得的期望收益为E1-Z,平均收益为,则其分别为:EZ=XY(R3+S3+S3-C3)+X(1-Y)(R3+S3-C3)+(1-X)Y(R3+S3-C3)+(1-X)(1-Y)(R3-C3)E1-Z=YZR3+Y(1-X)R3+(1-Y)(1-X)R3
3.2 博弈主體的稳定均衡策略分析
3.2.1 生产主体演化路径分析
生产主体的复制动态方程为:
令,求得的解即为可能的均衡点:
(1)当时,F(X)=0,表明X轴上所有点都处于稳定状态,即此时生产主体的策略选择比例不会随时间发生变化。
(2)当时,得到解X=0与X=1,为F(X)的两个可能的稳定态均衡点,需进一步判定,即对F(X)求导,当时,最终的结果为演化稳定策略(ESS)。对F(X)求导:
当时,此时,,所以X=0为生产主体的稳定策略,说明当生产主体因合作产生的成本大于收益时,选择不合作策略。
当时,此时,,所以X=1为生产主体的稳定策略,说明当生产主体因合作产生的收益大于成本时,选择合作策略。
3.2.2 加工主体演化路径分析
加工主体的复制动态方程为:
由上述分析可知,当F(Y)=o且时,达到演化稳定。
(1)当时,F(Y)=0,表明Y轴上所有点都处于稳定状态,即此时加工主体的策略选择比例不会随时间发生变化。
(2)当时,对F(Y)求导:
当时,此时,,所以Y=0为加工主体的稳定策略,说明当加工主体因合作产生的成本大于收益时,选择不合作策略。 当时,此时,,所以Y=1为加工主体的稳定策略,当加工主体因合作产生的成本小于收益时,选择合作策略。
3.2.3 销售主体演化路径分析
销售主体的复制动态方程为:
由上述分析可知,当F(Z)=o且时,达到演化稳定。
(1)当时,F(Z)=0,表明Z轴上所有点都处于稳定状态,即此时销售主体的策略选择比例不会随时间发生变化。
(2)当时,对F(Z)求导:
当玛时,,此时,,所以Z=0为销售主体的稳定策略,说明当销售主体因合作产生的成本大于收益时,选择不合作策略。
当时,此时,所以Z=1为销售主体的稳定策略,说明当销售主体因合作产生的成本小于收益时,选择合作策略。
3.3 各主体博弈系统稳定性分析
生产主体、加工主体、销售主体的复制动力系统为:
在该系统中,令F(X)=F(Y)=F(Z)=0,可以得到局部均衡点:A1(0,0,0),A2(0,0,1),A3(0,1,0),A4(0,1,1),A5(1,0,0),A6(1,0,1),A7(1,1,0),A8(1,1,1)。对于8个均衡点,可以利用雅可比矩阵进行局部稳定性分析,根据演化博弈理论,当均衡点的特征值都为负时,为系统的演化稳定点。该系统的雅可比矩阵为:
首先分析均衡点E1(0,0,0)的情况。此时的雅可比矩阵为:
此时雅可比矩阵的特征值为λ1=-C1,λ2=-C2,λ3=-C3。以此类推,将剩余的7个均衡点分别代入雅可比矩阵中,可以分别求出均衡点所对应的雅可比矩阵的特征值。如表2所示。
从上述分析和表2可知,三方演化博弈系统存在两个渐进稳定点:均衡点A1(0,0,0),即生产主体、加工主体和销售主体均采取“不合作”策略,不能建立信息共享的合作关系,无法达到合作共赢的局面;A8(1,1,1),即生产主体、加工主体和销售主体均采取“合作”策略,建立了信息共享的合作关系,构建了完整的产业链,能够实现合作共赢的局面。
3.4 各主体合作演化博弈数值仿真
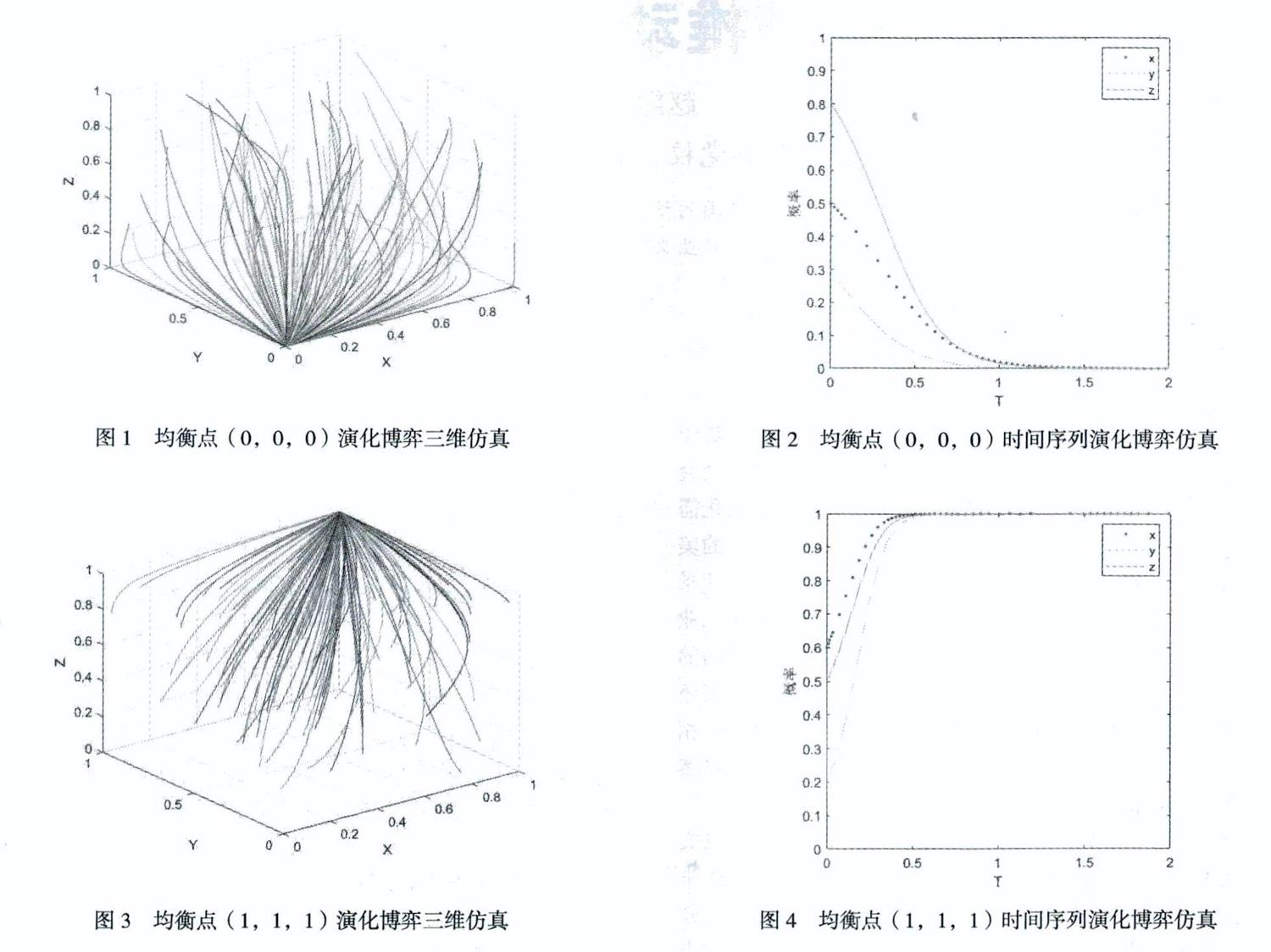
借助MATLAB软件进行仿真,通过模拟任意初始点向均衡点演化的轨迹,来判断以上论述的正确性。当,时,设R1=15、R2=14、R3=16、S1=2、Si=3、S2=2、Si=2、S3=2、Si=1、C1=5、C2=1、C3=1,此时,随机选取100组初始概率进行仿真,结果如图1所示,系统收敛于演化稳定点A1(0,0,0)。随机选取初始点X=0.5、Y=0.3、Z=0.8,仿真初始时间为0,结束时间为2,进行仿真,可得到三方的长期演化结果:收敛于(0,0,0)点,即三方均不合作,如图2所示。
当,时,设R1=15、R2=14、R3=16、S1=8、Si=9、S2=7、Si=8、S3=6、Si=9、C1=1、C2=1、C3=1,此时,随机选取100组初始概率进行仿真,结果如图3所示,系统收敛于演化稳定点A8(1,1,1)。随机选取初始点X=0.6、Y=0.2、Z=0.5,仿真初始时间为0,结束时间为2,进行仿真,可得到三方的长期演化结果:收敛于(1,1,1)点,即三方均合作,结果如图4所示。
MATLAB的仿真结果均符合上文中演化博弈分析的结论。
4 结论
通过分析可知,产业链中各主体是否采用合作策略,能够获得更多的利润是企业选择合作的关键要素,能够获得更多利润则合作可能性就大。合作是构建种养加销一体化生态循环农业模式的基础,其本质是各合作主体为了共同的目標相互影响、相互协调。
影响各主体达成合作关系的因素有很多,根据来源不同,可以将其分为内部因素和外部因素。内部因素可理解为各主体可操控的因素,各主体首先产生合作的需求,如在经济方面追求更高的利益,在生产方面选择更绿色、高效的方式;在拥有明确的合作需求后会对合作的具体内容进行商讨与制定,明确各主体在不同环节进行资源的共享。各主体要达成合作关系,首先要有合作意向,通过商讨和谈判确定合作理念、合作目标,各合作主体从事生产活动的目的都是获得利益,在发展过程中始终不变的最终目标都是使自身利益尽可能的增加从而获得利益最大化,这是能否在市场中继续生存、发展的根本所在,所以他们的首要考虑就是利益的获取。当他们可以通过合作获取更多的利益时,就会产生积极参加的意愿和行为,所以,各合作主体对物质利益的追求是促成合作关系必不可缺的动力,也是保持合作关系稳定持久的最直接因素。
[参考文献]
[1]Castro Antonio J,L 6 pez-Rodr f guez Mar f a D,Giagnocavo Cynthia, etal. Six Collective Challenges for Sustainability of Almer I a CreenhouseHorticulture.[J]. International journal of environmental research andpubliC health,2019(21).
[2]Anne-Kristin Lees. Steffen Adler. Increased utilisation of renewableresources: dilemmas for organic agriculture[J].Organic Agriculture,2019(04).
[3]Boone Lieselot, RoldAn-Ruiz Isahel, Van Linden Veerle, Muylle Hilde,Dewulf Jo. Environmental sustainability of conventional and organicfarming:Accounting for ecosystem 8ervices in life cycle且sses.ment.[J].The 5Gience of the tot8l environment.2019(10).
[4]Milutin Stojanovic.Biomimicry in Agriculture:Is the EcologicalSystem—Design ModeI the Future Agricultural Paradigm?[J].Journal ofAgricuhural and Environmental Ethics,2019(06).
[5]詹国辉.不完全契约、利益互动博弈与农村集体行动[J],世界农业,2019(08).
[6]屠文娟,钟辉,徐兰.基于供应链视角的农民专业合作社利益分配机制研究[J].江苏大学学报(社会科学版),2019(04).
[7]张笑寒,汤晓倩.农民专业合作社联合社成员“搭便车”行为研究——基于演化博弈视角[J].华中农业大学学报(社会科学版),2019(04).
[8]柳键,曾剑锋.政府监管与绿色生产多阶段博弈行为[J].系统工程,2014(08).
[9]陈莫凡,陈长塔,政府干预下农产品绿色供应链演化博弈分析[J].武汉理工大学学报(信息与管理工程版),2017(01).
[10]梁雯,陈广强,袁帅石.“农户——农产品加工中心”二级供应链激励契约研究——基于Rubinstei耐价还价博弈模型[J].哈尔滨商业大学学报(社会科学版),2017(02).
[11]李泉林,张玉,鄂成国.多个农民专业合作社和多个超市的网络博弈研究[J].系统工程学报,2019(01).
[12]周业付.虚拟农产品供应链合作联盟构建及利益博弈[J].华东经济管理.2018(12).
[13]姜吴.农产品供应链视角下农户联盟绩效最优模式研究[J].商业经济研究,2019(07).
